Předminulý týden oznámila skupina mladých výzkumníků na Technické Univerzitě v holandském Delftu (TU Delft) pod vedením (také mladého) profesora Ronalda Hansona výsledky svého experimentu, kterým opět potvrdila neplatnost Bellových nerovností, a tím i neplatnost jakýchkoliv klasických alternativ ke kvantové teorii. Jejich výsledek je zajímavý tím, že eliminoval zbývající skuliny v předchozích podobných experimentech, a tím zhatil poslední naděje těch, kteří doufali, že kvantovou teorii bude možné nahradit nějakou jinou a přitom klasickou teorií. Ačkoliv je výsledek Hansonova týmu založen spíše na evoluční než revoluční obměně předchozích experimentů, přesto se stává důležitým milníkem, který definitivně ukončuje debatu o principech, na kterých kvantová teorie může či nemůže stát.
Pokusme se ale nejprve přiblížit podstatu letitého sporu, který byl delftskými výzkumníky definitivně uzavřen.
Už více než sto let poutá kvantová teorie svými kontraintuitivními předpověďmi zájem celé řady fyziků, počínaje Albertem Einsteinem a Nielsem Bohrem, kteří spolu strávili dlouhé disputace nad tím, zda její výsledky jsou fyzikálně akceptovatelné či nikoliv. Albert Einstein byl dlouhodobě nespokojený s podobou kvantové teorie, a pokoušel se ukázat, že tato teorie odporuje základním principům, které podle něj měla ctít každá akceptovatelná fyzikální teorie. Ve snaze dokázat logickou nekonzistenci kvantové teorie zkonstruoval Einstein spolu se svými spolupracovníky Borisem Podolským a Nathanem Rosenem myšlenkový experiment, který, pokud by platila pravidla kvantové teorie, dával podle něj zcela nesmyslný výsledek. Tento myšlenkový experiment vešel ve známost jako tzv. Einstein-Podolského-Rosenův paradox (či kratčeji EPR paradox).
V EPR paradoxu máme elektron-pozitronový pár, který byl vytvořen nejlépe kreací ze srážky protiběžných gama fotonů o stejné energii a opačných hybnostech (jedná se pouze o myšlenkový experiment, ačkoliv dnes umíme elektron pozitronové páry rutinně připravovat, děláme to mnohem efektivněji ve srážkách gama fotonů s atomovými jádry). Protože podle předpokladů byla úhrnná hybnost obou gama fotonů nulová, je tím pádem nulová i úhrnná hybnost vzniklého elektronu a pozitronu, které se tedy od místa svého vzniku vzdalují stejnými, ale opačně orientovanými rychlostmi. Kromě zákona zachování energie a hybnosti musí ale také platit zákon zachování momentu hybnosti, a protože do momentu hybnosti přispívá i vnitřní moment hybnosti částic, tzv. spin, musí mít elektron a pozitron vzájemně opačně orientované spiny.
Spin je typická kvantová vlastnost, která nemá v klasické fyzice žádnou dostatečně přiléhavou analogii. Po jeho objevu ve slavném Sternově-Gerlachově experimentu v roce 1922 se následně zjistilo, že spin mají všechny částice včetně elektronů a fotonů. Později se vyjasnilo, že konkrétně u fotonů spin souvisí s polarizací světla – přesněji řečeno, o spinu se bavíme jako o vlastnosti jednotlivých částic, zatímco u letících svazků částic o stejném spinu hovoříme o polarizaci svazku. Anebo ekvivalentně, u světla můžeme spin chápat jakožto mikroskopickou vlastnost fotonů, kterou makroskopicky pozorujeme jako polarizované světlo (nepolarizované světlo je pak tvořeno fotony majícími nestejné spiny). Tato terminologie se následně přenesla opačným směrem z optiky do fyziky elementárních částic, a proto, když čteme o srážkách polarizovaných svazků těch či oněch částic v urychlovačích anebo o polarizovaných terčích při jejich bombardování částicemi, máme tím na mysli, že spiny částic v příslušných svazcích či spiny jader atomů v terčích mají díky předešlé přípravě stejnou orientaci.
|
Plaketa na Frankfurtském Institutu připomínající experiment Otto Sterna a Waltera Gerlacha (Stern vlevo). Kredit: Wikimedia Commons. Další osudy obou protagonistů se ubíraly po naprosto odlišných cestách. Po převzetí moci nacisty v roce 1933 odešel Otto Stern do USA, kde působil nejprve jako profesor na Carnegieho Technologickém Institutu, a později jako emeritní profesor na Kalifornské Univerzitě. Walter Gerlach se naopak aktivně angažoval v nacistickém Německu a stal se dokonce jednou z nejvýše postavených osob zodpovědných za vývoj nacistické atomové bomby. Na konci války byl Brity a Američany spolu s dalšími německými atomovými vědci zajat a osm měsíců internován, aby jej nezískali Sověti. V roce 1957 pak spolupodepsal tzv. Göttingenský manifest proti vyzbrojení Německé Spolkové Republiky atomovými zbraněmi. |
Podstatu výše zmíněného EPR experimentu je nemožné pochopit bez znalosti dvou klíčových vlastností spinu. Jednou je tzv. nekompatibilita měření průmětů spinu do různých os, a tou druhou je kvantování hodnot jeho průmětu. U obou vlastností se zastavíme, protože obě se prolínají celým zbytkem tohoto textu.
Nejprve se zmiňme o nekompatibilitě průmětů spinu do různých os. V souladu se Sternovým a Gerlachovým experimentem je spin podobně jako polarizace světla směrová vlastnost, kterou bychom tedy měly popsat nějakým vektorem (čili orientovanou úsečkou), který by odrážel směr spinu a jeho velikost. Každý vektor můžeme popsat jeho složkami, což jsou vlastně jeho průměty do námi zvolených souřadnicových os. Vektory jsou nedílnou součástí popisu jak Newtonovské fyziky, tak speciální i obecné teorie relativity, popisujeme pomocí nich rychlosti a zrychlení částic, jejich hybnosti, síly na ně působící, ale také intenzity různých polí, jako je elektrické či magnetické, a mnoho jiných fyzikálních veličin.
Zatímco ale v klasické fyzice není problém změřit všechny tři složky libovolné vektorové fyzikální veličiny, v případě spinu to nelze. Ukazuje se totiž, že pro jednotlivé složky spinu platí Heisenbergův princip neurčitosti, analogicky, jako tento princip platí pro polohu a hybnost částice. Připomeňme krátce, že Heisenbergův princip pro polohu a hybnost říká, že čím přesněji určíme polohu částice, tím neurčitější se stává výsledek následného měření její hybnosti, a naopak. Podobný vztah se dá získat (a experiment jej plně potvrzuje) i pro složky spinu, kdy jakmile určíme přesně složku v jednom směru, ovlivní to rozptyl výsledků při následném měření zbylých složek.
Druhou klíčovou vlastností spinu je kvantování velikostí jeho složek. Tato vlastnost je pro změnu zase podobná s kvantováním energetických hladin v atomu, kdy se elektron může v atomu vyskytovat jen s určitými diskrétními hodnotami energie. Diskrétní energetické hladiny tvoří jakýsi čárový kód povolených energií, který je unikátní pro každý prvek či chemickou sloučeninu, na kterémžto faktu je založena spektroskopie umožňující identifikaci látek analýzou jimi vyzářeného či pohlceného světla. V případě složek spinu je ale povolené množství jeho hodnot mnohem chudší, konkrétně pro elektrony jenom +1/2 a -1/2. Totéž platí pro protony, neutrony, a dále obecně pro všechny elementární fermiony, jako jsou třeba kvarky a neutrina. Naopak složky spinu pro elementární bozony, jako jsou fotony, gluony nebo tzv. intermediální výměnné bozony zodpovědné za slabou interakci částic, nabývají hodnot +1 nebo -1 (v případě intermediálních bozonů mohou nabývat ještě hodnoty 0, kterážto hodnota je pro nehmotné bozony nepřípustná).
Právě zmíněné dvě vlastnosti spinu, totiž nekompatibilita jeho složek plus kvantování jejich hodnot, dává vznik docela zvláštnímu chování při jeho měření, jak nyní popíšeme:
- provedeme-li měření průmětu spinu elektronu ve směru nějaké osy, dostaneme tedy vždy výsledek +1/2 nebo -1/2
- pokud následně provedeme druhé měření téže složky, dostaneme vždy už tutéž hodnotu. Jinými slovy, zatímco u prvního měření jsme pro některé z elektronů dostali výsledek +1/2, a pro ostatní výsledek -1/2, tak u druhého a dalšího měření už dostáváme pro každý z měřených elektronů už tentýž výsledek, jako v měření předešlém
- pokud ale provedeme měření jiné složky spinu, než v předcházejícím měření, tak opět dostáváme zcela náhodně pro některé z elektronů výsledek +1/2 a pro ostatní -1/2.
Pro lepší představu je chování spinu při opakovaných měřeních ilustrováno na následujícím obrázku.
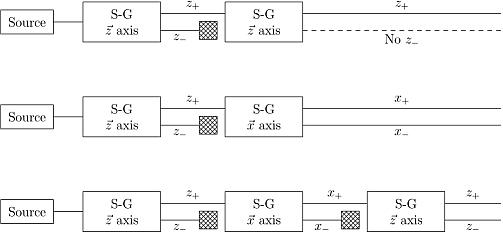
Ilustrace chování spinu při opakovaných měření ve Sternově-Gerlachově experimentu:
Nahoře je opakované měření ve směru osy z, získají se hodnoty průmětu spinu +1/2 a -1/2, označené na obrázku jako z+ a z-. Vybere se hodnota z+, ta pokračuje do dalšího měření ve směru téže osy. Výsledkem je opět táž hodnota, tzn. opakované měření beze změny osy dává identické výsledky jako měření první.
Uprostřed je měření ve směru osy z, následované měřením ve směru osy x. V prvním měření se opět vyfiltruje pouze hodnota z+, která se pošle do druhého Sternova-Gerlachova přístroje. Průmět spinu ve směru osy x je veličinou nekompatibilní s jeho průmětem do osy z, proto je neurčitost druhého měření ve shodě s Heisenbergovým principem neurčitosti rozmazána, a proto se dostanou se stejnou pravděpodobností opět obě hodnoty +1/2 a -1/2, označené jako x+ a x-.
Dole je měření ve směru osy z, následované měřením ve směru osy x, a poté opět ve směru osy z. Po druhém měření se ponechá jenom složka x+, která se pošle do třetího Sternova-Gerlachova přístroje. Výsledkem jsou opět dvě hodnoty z+ a z-. Kredit: Wikimedia Commons
Výše uvedené dvě vlastnosti spinu jsou tou zásadní ingrediencí v EPR experimentu, bez nich by totiž žádný paradox vůbec vzniknout nemohl. Máme elektron a pozitron pohybující se od sebe, přičemž víme, že součet jejich spinů musí být nulový kvůli zákonu zachování momentu hybnosti. Změříme např. u elektronu spin ve směru nějaké zvolené osy, dejme tomu ve směru osy z. Pro tuto z-ovou složku spinu dostaneme jeden ze dvou možných výsledků, dejme tomu +1/2. Díky nulovosti úhrnného momentu hybnosti tím pádem víme, že pozitron musí mít této složky opačnou, tedy -1/2. Elektron tímto měřením zároveň přešel do stavu s hodnotou průmětu spinu +1/2, o čemž se můžeme přesvědčit opakovaným měřením provedeným na tomto elektronu. Vzdálený pozorovatel provádějící na pozitronu stejná měření nám podobně může potvrdit, že on zase dostává opakovaně při měření průmětu spinu pozitronu do směru osy z hodnotu -1/2. Tuto situaci můžeme statistickou terminologií okomentovat tak, že pokud pozorovatel A i B provádí měření stejné složky (tj. průmět spinu do stejné osy), tak jsou jejich výsledky stoprocentně antikorelované.
Pokud by ale pozorovatel B měřil jinou složku než pozorovatel A, dejme tomu y-ovou, tak pak by v polovině případů, kdy A naměřil +1/2, dostal +1/2, a v druhé polovině případů -1/2. Úplně stejně by to dopadlo pro případy, ve kterých by pozorovatel A naměřil -1/2; opět by v polovině těchto případů dostal pozorovatel B výsledek +1/2, ve zbytku pak -1/2. Tuto situaci bychom opět mohli statistickou terminologií okomentovat tak, že v tomto případě mají výsledky obou pozorovatelů nulovou korelaci, tedy že jsou naprosto nezávislé jeden na druhém. Pro lepší představu si opět právě popsané chování ilustrujme na následujícím obrázku.
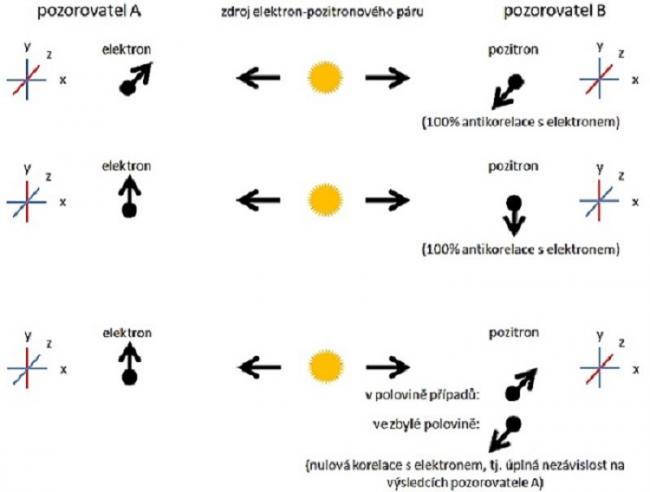
Ilustrace zdánlivého okamžitého přenosu informace v EPR paradoxu:
- v prvých dvou případech měří oba pozorovatelé stejnou složku spinu (nahoře z-ovou, níže y-ovou), a jejich výsledky jsou stoprocentně antikorelované
- ve třetím případě měří každý z pozorovatelů jinou složku spinu (pozorovatel A y-ovou, pozorovatel B z-ovou), a jejich výsledky jsou na sobě nezávislé, tj. mají nulovou korelaci
(kredit: autor)
A o tom je celý EPR paradox, zbývá totiž už jen dodat, že podle kvantové teorie budou oba pozorovatelé dostávat právě popsané výsledky i tehdy, když je budou provádět současně nebo v tak malém časovém odstupu, že signál letící světelnou rychlostí by nestihl přenést informaci s výsledkem jednoho pozorovatele k tomu druhému. A to zní krajně podezřele, speciálně pak pro Alberta Einsteina jakožto otce speciální teorie relativity, která přenosy informací nadsvětelnou rychlostí striktně zakazuje. Hlubším rozborem se dá sice ukázat, že okamžitá změna stavu vzdáleného pozitronu žádnou informaci přenést nemůže, nicméně samotná možnost, že stav vzdálené částice se změní okamžitě, je věcí odůvodněně podezřelou. Einstein takovou nelokální změnu nazval strašidelným působením na dálku, a odmítl přistoupit na myšlenku, že by akceptovatelná fyzikální teorie mohla něco takového obsahovat.
Bylo by dobré si na druhou stranu osvětlit, proč přitom nemůže dojít k přenosu informace od elektronu k pozitronu, a to ačkoliv se stav vzdáleného pozitronu mění už v okamžiku změření spinu elektronu. Klíčem je náhodnost výsledků jednotlivých měření. U nově vygenerovaného elektron-pozitronového páru je totiž výsledek měřením kterékoliv spinové složky zcela náhodný. Zkusme si přesto představit, že se pozorovatel B bude snažit zjistit, které složky spinu se pozorovatel A rozhodl měřit. Udělají dlouhou řadu měření, kterou rozdělí dejme tomu do sad vždy 40 po sobě jdoucích měření, a dohodnou se na tom, že v rámci těchto sad budou měřit vždy stejnou složku, jinak se ale budou rozhodovat zcela autonomně, jakou složku budou měřit. Tzn. že osu měření mohou změnit např. přesně po 40-tém., nebo 80-tém, 120-tém atd. měření, ale ne mezi těmito mezemi. Oba dva pozorovatelé si na začátku sesynchronizují své hodiny, rozejdou se na svá od sebe vzdálená pracoviště, a každé měření provedou v přesně stejný okamžik. Zaznamenají výsledky svých měření, a po skončení odešle pozorovatel A druhému pozorovateli své výsledky, ale bez informace, kterou složku spinu v té které sadě měřil. Pozorovatel B ale porovnáním výsledků i tak spolehlivě pozná, ve kterých sadách měřil pozorovatel A ve stejné ose jako on, protože taková sada bude dokonale antikorelovaná k jeho vlastní sadě (pravděpodobnost náhodné shody je pouze jednu ku biliónu, přesně 1 ku 2^40). Situaci opět ilustruje následující obrázek.
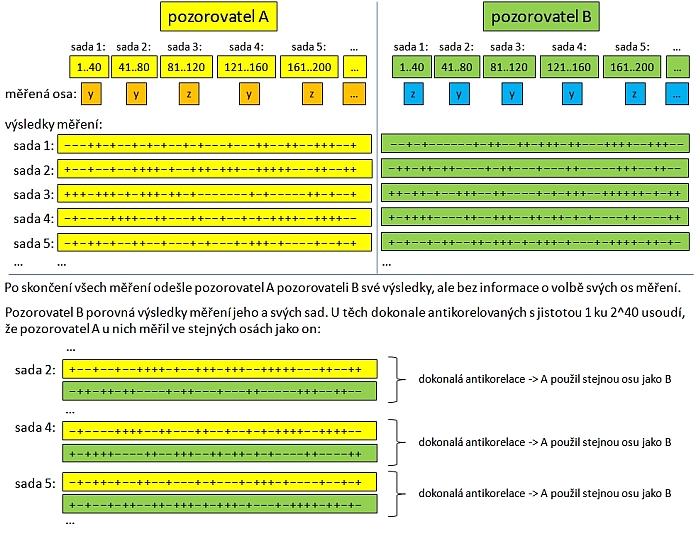
Vliv volby vzdálených měření na korelaci měřených hodnot. Dva pozorovatelé provádějí měření průmětů spinů částic v dlouhé řadě EPR experimentů, kterou rozdělili do sad po 40 měřeních. Uvnitř každé sady volbu svého měření podle své dohody nemění, na začátku každé sady se ale autonomně a na poslední chvíli rozhodnou, kterou spinovou složku budou měřit. Svá měření zaznamenávají, a po skončení měření všech sad pozorovatel A odešle své výsledky pozorovateli B, ale bez informace o své volbě os pro jednotlivé sady. Pozorovatel B porovná výsledky pro každou sadu zvlášť, a s vysokou jistotou odhalí, u kterých sad měřil pozorovatel A ve stejných osách, jako on sám.
To, co je na tomto výsledku z klasického pohledu podezřelé, je právě ten „vznik“ antikorelace u těch sad, kde oba pozorovatelé použili stejnou osu pro měření průmětu spinu. Své rozhodnutí totiž dělají ve stejný okamžik a mohou být od sebe i velice vzdáleni, takže obě části systému se nemohou nijak „domluvit“, pokud by přitom měly respektovat rychlost světla jakožto maximální rychlost. Přesto všechno tyto záhadně vznikající a mizející antikorelace nemohou být nijak použity pro přenos informace nadsvětelnou rychlostí, protože mohou být prokázány až poté, co pozorovatel B dostane od pozorovatele A jeho výsledky klasickou cestou, tedy maximálně světelnou rychlostí. Do té doby drží pozorovatel B v ruce pouze náhodnou sekvenci dat, z níž samotné nemůže žádnou informaci vyčíst.
(Kredit: autor)
Pozorovatel B sice pozná, u kterých sad použil pozorovatel A stejné osy, ale pozná to až poté, co mu A odešle své výsledky měření. Teprve potom je může porovnat se svými a antikorelované sady identifikovat. Do té doby, než mu výsledky od pozorovatele A dorazí, má v ruce jenom náhodnou řadu dat, ze kterých nemá šanci žádnou informaci vyčíst. To podivné na celé té věci je, že to, zda bude ta která sada antikorelovaná či ne, rozhodnou svou volbou pozorovatelé ve stejný čas, ale přitom mohou být velice vzdáleni. Klasická fyzika takový výsledek nepřipouští, protože jedna z oddělených částí systému nestihne „dát vědět“ té druhé části o změněné konfiguraci měřicího přístroje žádnou interakcí na pozadí, pokud je tato interakce přenášena maximálně rychlostí světla. Přesto všechno spor se speciální teorií relativity nemůže vzniknout, protože přes tuto podivnost nelze zmíněné antikorelace žádným způsobem využít k přenosu informace nadsvětelnou rychlostí. Pozorovatel B musí totiž nejprve počkat, až mu klasickou cestou dojdou data zaznamenaná pozorovatelem A, a teprve ta mu poslouží jako klíč k rozšifrování chování pozorovatele A.
Je to zkrátka a dobře náhodnost, která v případě tzv. EPR paradoxu zachraňuje zadek speciální teorii relativity a jejímu světelnému rychlostnímu limitu na přenos informace. Anebo jinak řečeno, náhodnost je to, co umožňuje oběma teoriím, kvantové teorii i speciální teorii relativity, aby spolu koexistovaly bez logických rozporů.
Přesto všechno nebyl Albert Einstein s podobou kvantové teorie spokojen. Mimochodem, EPR paradox nebyl jeho prvním ani posledním pokusem o zpochybnění kvantové teorie, první adresoval už v roce 1927 během páté Solvayské fyzikální konference, druhý pak v roce 1930, a v obou případech se Niels Bohr musel obrazně řečeno docela zapotit, než se mu podařilo Einsteinovy sofistikované argumenty vyvrátit. EPR paradox vzniklý v roce 1935 byl třetím takovým Einsteinovým pokusem, a na rozdíl od jeho dvou předchozích, kdy Bohr nakonec triumfoval, tento skončil jakýmsi patem – Einsteinovi se sice podařilo zkonstruovat myšlenkový experiment, na němž Bohr na rozdíl od předchozích dvou případů nenalezl žádné chyby v předpokladech, oba fyzikální velikáni se ale rozešli v tom, jestli je či není možné výsledek EPR experimentu považovat za akceptovatelný. V té době navíc neexistovala žádná realistická možnost, jak spor experimentálně rozsoudit.
Historická vsuvka:

V debatě Bohra a Einsteina vystupoval Bohr jako velice zdatný advokát kvantové teorie, ve skutečnosti ale Einsteinovi na kvantové teorii nejvíce vadil Heisenbergův princip neurčitosti. Připomeňme, že právě ten ovlivňuje jednu ze dvou klíčových vlastností spinu, kterou je právě nekompatibilita měření průmětů spinu v různých osách, a ta se v EPR experimentu zase odráží v antikorelacích při měření ve stejných osách, případně v nulové korelaci při měření v na sebe kolmých osách. Einstein se s Heisenbergovým principem neurčitosti nikdy nesmířil, podle něj byl znakem neúplnosti kvantové teorie, která by měla být nahrazena nějakou úplnou teorií, ve které by princip neurčitosti neměl místo. Přesto mezi Einsteinem i Heisenbergem vládl velice korektní vztah naplněný vzájemným respektem, a to navzdory dramatickým momentům, které poznamenaly jejich setkání. Heisenberg už jako gymnazista nadšeně hltal Einsteinovy články o speciální teorii relativity, a velice stál o to, aby byl o generaci starším Einsteinem uznán. Heisenberg byl svým způsobem zázračné dítě, doktorát získal ve 22 letech a habilitoval o rok později. Jeho podíl na vzniku moderní kvantové teorie lze jen těžko přecenit - tzv. starou kvantovou teorii, což byla jen klasická mechanika doplněná o pár nesystémových výběrových pravidel pro odůvodnění existence diskrétních energetických hladin atomu, nahradil jím vytvořenou tzv. maticovou mechanikou, díky které objevil existenci nekompatibilních proměnných a došel i ke svému slavnému principu neurčitosti. Stál také za mnoha průlomovými pracemi v atomové a zvláště jaderné fyzice, poprvé správně popsal podstatu feromagnetismu, položil základy relativistické kvantové teorie pole, což je teoretický rámec pro popis elementárních částic včetně procesů jejich kreace a anihilace, dále úspěšně popsal procesy absorpce světla atomy a jeho vyzařování, a výčet jeho vědeckých úspěchů by takhle mohl ještě dlouho pokračovat. Své teorie a nápady posílal Einsteinovi, který se k nim ovšem stavěl čím dál tím více rezervovaně, protože se více a více vzdalovaly od jeho vlastního pojetí fyziky. V roce 1922 se měli poprvé setkat na fyzikální konferenci v Lipsku, ale všechno dopadlo jinak. Při vstupu do konference byl Heisenbergovi vnucen nenávistný pamflet proti Einsteinovi, podepsán německým nositelem Nobelovy ceny Philippem Lenardem a osmnácti dalšími německými vědci. Krátce předtím byl nacistickým komandem zavražděn Einsteinův blízký přítel, německý ministr zahraničí Walther Rathenau, a Albert Einstein figuroval na zveřejněném seznamu budoucích židovských obětí tohoto komanda, proto svou účast na konferenci okamžitě zrušil. Tehdy 21 letý Heisenberg prý byl otřesen takovýmto politickým útokem, nicméně odvahu k jeho veřejnému odsouzení nenašel on, ale jeho o generaci starší přítel Max von Laue, který si dokázal udržet svůj odvážný postoj i mnohem později, ve velice nebezpečných dobách vlády nacistů. Přesto všechno Einstein s Heisenbergem nadále korespondoval, a ačkoliv s ním ve svých odpovědích čím dál více nesouhlasil, navrhl jej dokonce v roce 1928 na Nobelovu cenu za fyziku, kterou o čtyři roky později nakonec Heisenberg dostal. Proti Heisenbergovi byla od roku 1933 vedena nenávistná kampaň, která vyvrcholila v roce 1937 jeho nařčením mj. z „židovského myšlení“ v oficiálním žurnálu SS. Po takových útocích většinou následovala návštěva pánů v kožených kabátech, a dotyčného nešťastníka pak už kolikrát nikdo nikdy nespatřil. Takovému konci zamezila návštěva Heisenbergovy maminky u matky Heinricha Himmlera, jelikož se obě znaly přes Heisenbergova pradědečka a Himmlerova dědečka, oba kamarády z turistického klubu. Himmler následně poslal jeden dopis Reinhardu Heydrichovi, ve kterém napsal, že Německo si nemůže dovolit ztratit Heisenberga, protože pro ně může být užitečný. Ve druhém dopise poslaném Heisenbergovi mu radil, že musí umět oddělovat profesionální znalosti jiných vědců od jejich osobních a politických postojů. O pár let později bylo na Heisenberga vzpomenuto v souvislosti se zahájením nacistického projektu na výrobu atomové zbraně, a Heisenberg se nezpěčoval – ale to už je jiný příběh.
Bohrova a Einsteinova debata rozpoutala rozsáhlou diskuzi v celé fyzikální komunitě, přičemž závěry obou fyziků byly vydestilovány do podoby několika málo principů, kterým měla každá akceptovatelná fyzikální teorie podle Einsteina vyhovovat, zatímco kvantová teorie jim nevyhovovala. Jednalo se zejména o tzv. princip realismu a princip lokality.
Princip realismu požaduje, aby každé měřitelné veličině, tedy i spinu částic, odpovídalo „něco skutečného“, co existuje nezávisle na měření. Výsledek každého měření by tedy měl být dán už před samotným měřením, a např. volba měřené pozorovatelné by ho neměla narušit. Je evidentní, že už tento samotný požadavek není slučitelný s Heisenbergovým principem neurčitosti, který tvrdí, že měření jedněch veličin ovlivní neurčitost měření jiných, s nimi nekompatibilních veličin.
Princip lokality potom požaduje, že pokud jsou dvě části systému separovány, jako např. elektron a pozitron poté, co se dostatečně vzdálí z místa svého zrodu, tak potom měření na jednom z nich nijak nesmí ovlivnit stav druhé, vzdálené části systému.
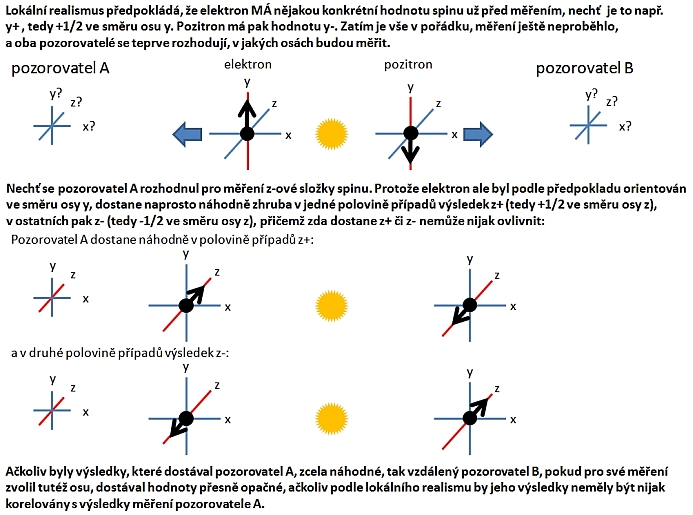
Konflikt EPR experimentu s lokálním realismem.
Protože jsou výsledky měření v osách kolmých na směr spinu dokonale náhodné, tak je podle klasické teorie nevysvětlitelné, jak může vzdálený pozorovatel B, pokud měří ve stejné ose, dostávat 100% antikorelaci s výsledky pozorovatele A. Kredit: autor
Fyzikální komunita se následně rozštěpila na přívržence kvantové teorie v její stávající podobě, a na přívržence různých lokálně realistických alternativ ke kvantové teorii, jako byly např. modely s tzv. skrytými proměnnými. Druhá skupina prohlašovala, že kvantová teorie je neúplná, a že např. Heisenbergův princip neurčitosti je pouhý důsledek toho, že neznáme hodnoty nějakých dnes skrytých proměnných, které mohou být měřením nechtěně ovlivněny a které mohou v důsledku změnit dynamiku systému tak, že se efektivně chová právě tak nepochopitelně, jak to kvantová teorie předpovídá.
Dlužno ovšem říct, že většina kvantových fyziků si s principy stojícími v základech kvantové teorie hlavu zase až tak moc nelámala, a věnovala se raději praktickým aplikacím kvantové teorie, které přibývaly jako houby po dešti. Kvantová teorie se v té době stala nezastavitelným parním válcem (který se mimochodem dodnes nezastavil), který úspěšně projel mnoha obory fyziky i chemie. Denně přibývaly další její úspěšné aplikace nejen v teorii elementárních částic a v jaderné a atomové fyzice, ale také ve fyzice pevných látek, při popisu supravodivosti, supratekutosti, ale i obyčejné elektrické vodivosti, při popisu polovodičů, ve spektroskopii, kvantové chemii, elektronice, laserové fyzice, krystalografii, fotonice, a tak by se dalo pokračovat dlouho. Proč se tedy mořit s abstraktními aspekty kvantové teorie, když výzkum denně ukazuje neuvěřitelnou předpovědní sílu kvantové teorie?
Uplynula další skoro tři desetiletí, než se spíše filosofickou rozepři Bohra a Einsteina podařilo přeformuloval do podoby experimentu, který by umožnil testovat dokonce ony dva zmíněné základní principy realismu a lokality. V roce 1964 se to podařilo Johnu Stewartu Bellovi, severoirskému fyzikovi. Bell matematicky exaktně dokázal, že jakákoliv teorie, která současně respektuje princip lokálnosti a princip realismu, musí vyhovovat jistým speciálním nerovnostem, které dnes nesou jeho jméno.
Bellovy nerovnosti se týkají maximálních hodnot jednoho výrazu, který je šikovně zkonstruován z korelačních funkcí výsledků měření provedeného na dvou oddělených místech. Lokálně realistické teorie dávají pro tento výraz jako jeho maximální hodnotu číslo 2, ale pro kvantovou teorii se dá ukázat, že v optimálně zvolených případech lze docílit až hodnoty odmocnina(2) krát větší, tedy zhruba 2,828. Pokud by pro tyto optimálně zvolené případy experiment dal hodnotu 2,828, tak by to sice ještě neznamenalo, že kvantová teorie je správná, nicméně spolehlivě by to pohřbilo všechny lokálně realistické teorie, protože z premis lokálního realismu plyne limit 2 matematicky exaktně. Je to podobné, jako kdyby podle zvolených premis měla být nějaká hodnota třeba kosinem nějakého úhlu, ale její měření by dalo výsledek 1,3; nevyhnutelný závěr by byl, že výchozí premisa byla nutně špatně, protože kosinus žádného úhlu nemůže být větší než jedna.
Nerovnosti jsou ve své konkrétní podobě formulovány pro limitní hodnotu 2, tzn. že lokálně realistické teorie je nikdy nenarušují, kvantová teorie je ale narušuje v těch případech, ve kterých předpovídá hodnotu Bellova výrazu větší než 2. Narušení Bellových nerovností je tedy synonymem pro pohřeb lokálního realismu. Zbývá tedy už jen proměřit hodnotu Bellova výrazu v oněch rozhodujících případech, a tím i rozhodnout dávný spor Einsteina a Bohra.
Mohlo by se zdát, že odlišit experimentálně hodnotu 2 od 2,828 by neměl být takový problém. Ve skutečnosti to ale trvalo dalších dlouhých několik desítek let, než se experimentální technika dostala na takovou úroveň, aby Bellův test bylo možné provést. Problém je totiž v tom, že právě ty experimentální situace, pro které vychází hodnota Bellova výrazu jako větší než 2, jsou velice obtížně realizovatelné. Jsou k nim totiž potřeba tzv. entanglované čili provázané páry částic, přičemž navíc částice z každého takového páru musí být od dostatečně vzdálené – a především toto je velikým kamenem úrazu.
Jeden případ entanglementu jsme si už výše popsali, byl to právě onen elektron-pozitronový pár, který figuroval v myšlenkovém EPR experimentu. Pro praktické měření se ale entanglované elektron-pozitronové páry ani trochu nehodí, už jen kvůli tomu, že pozitron by v procesu měření velice ochotně anihiloval s prvním elektronem, na který by natrefil. Existuje ale možnost využít i jiné entanglované páry, např. dva elektrony nebo dva fotony. Dokonce lze entanglovat i spiny jader atomů sedících v uzlech krystalické mřížky, anebo spiny iontů lapených v uzlech „optických krystalů“, tedy uměle vytvořených mříží z laserových paprsků. Experimentátoři zabývající se entanglementem nejvíce milují pracovat s fotonovými páry, a to proto, že se jednoduše připravují, a navíc mají fotony další příjemnou vlastnost, v opticky průhledných prostředích interagují velice zanedbatelně (proto jsou také tato prostředí průhledná, naopak prostředí, se kterými fotony reagují významně, jsou buď neprůhledná anebo pouze průsvitná), a díky tomu si své vlastnosti uchovávají relativně dlouho nedotčené, takže jsou přístupné následnému měření. Navíc se fotony dají dobře posílat optickými vlákny, díky čemuž je experimentátoři snadno mohou nasměrovat přesně kam potřebují. V některých případech je ale naopak lepší pracovat s elektrony, protože fotony, jak známo, stále někam pospíchají a zastavit se je podaří pouze jejich absorpcí v látce, což pro ně znamená konečnou stanici na jejich celoživotní pouti. Oproti tomu elektron umí celkem spořádaně sedět buďto v nějaké krystalové vakanci, nebo v nějaké z mnohých rafinovaných pastí, a je ochoten snášet příkoří opakovaných měření, už jen proto, že částečnou diplomatickou imunitu bránící jeho snadnému zničení mu garantuje zákon zachování elektrického náboje.
Je nutné zmínit, že ne u každého měření prováděného na entanglovaných párech budou Bellovy nerovnosti narušeny. Tak např. nebudou narušeny v žádném z případů ilustrovaných výše, kdy pozorovatelé provádí měření buďto ve stejných osách, anebo v navzájem kolmých osách, a proto analýzou těchto situací nelze exaktně rozhodnout mezi kvantovou teorií a lokálně realistickými teoriemi (dá se ukázat, že v případech pospaných výše vyjde hodnota Bellova výrazu přesně 2). To se vzhledem k popsaným vlastnostem EPR experimentu může zdát zvláštní, vždyť jsme přece celou dobu tvrdili, že EPR experiment odporuje klasické fyzikální intuici, která v některých případech neumí vysvětlit antikorelaci vzdálených měření. Bellův vztah ale není o nějaké intuici, Bellův vztah je matematicky exaktně dokázaným vztahem plynoucím z exaktně formulovaných předpokladů. Jde tedy o situaci vzdáleně podobnou tomu, jako když nebylo možno usvědčit Al Caponeho ze zločinů, za nimiž nade vši pochybnost stál, ale podařilo se ho dostat za prokázané krácení daní, za což byl nakonec také odsouzen. Jinými slovy, zatím jsme si sice mohli celou dobu říkat, že výsledky EPR paradoxu jsou z hlediska klasické fyziky divné či krajně podezřelé, nicméně teprve až narušení Bellových nerovností je tím korunním důkazem, který prokazuje neplatnost lokálního realismu jako takového.
Nebudeme zde zabíhat do matematického rozboru Bellových nerovností, vystačme si pouze s tím, že jejich analýzou se dá ukázat, že maximální odchylka od klasického chování nastane tehdy, když pozorovatel B měří v osách o 45 stupňů pootočených vůči osám pozorovatele A. Přitom pozorovatel A provádí měření ve dvou různých polohách svých os, navzájem na sebe kolmých, a pozorovatel B také měří ve dvou různých na sebe kolmých polohách, které jsou ale o 45 stupňů pootočené vůči osám pozorovatele A. Celkem tedy existují čtyři kombinace volby os měření, jak ukazuje následující obrázek.
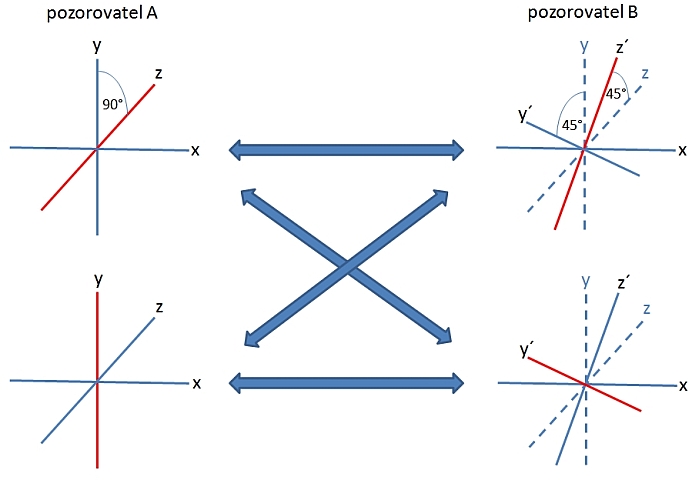
Volby měřených os potřebné pro testování Bellových nerovností.
Pozorovatel A měří ve dvou na sebe kolmých osách, např. y a z. Pozorovatel B měří také ve dvou na sebe kolmých osách, ty ale musí být pootočeny o 45 stupňů vůči osám použitým pozorovatelem A. Teprve tehdy se maximalizuje hodnota Bellova výrazu počítaného z korelací jednotlivých měření (pootočené osy jsou označené y´ a z´). Celkem existují 4 kombinace voleb os obou pozorovatelů. (Kredit: autor)
Provede se dostatečně dlouhá řada měření pro každou ze čtyř kombinací měřených os, a pro každou z těchto kombinací se spočte odpovídající korelační funkce ze získaných četností naměřených průmětů obou spinů. Pro každé nastavení os lze dostat celkem čtyři možné kombinace výsledků, tak např. pro volbu os z a z´ jsou to kombinace [z+;z´+], [z+;z´-], [z-;z´+], [z-;z´-] (celkem tedy existuje 16 různých variant nastavení měřených os a získaných výsledků). Ze čtyř korelačních funkcí se pak vypočte onen klíčový výraz, jehož hodnota pak rozhodne, jestli byly či nebyly Bellovy nerovnosti narušeny.
Dřívější testování Bellových nerovností sice už celkem spolehlivě prokázalo jejich narušení, přesto ale ponechávalo aspoň malilinkou naději přívržencům lokálního realismu. Vždycky totiž zbyla nějaká skulina, která mohla být využita, i když spíše jako zoufalý protiargument než jako seriózní zpochybnění výsledků testování. Jedna z typických těžkostí při testování s použitím entanglovaných fotonů byla nedostatečná účinnost detektorů, které v některých případech foton nezaznamenaly. Nejde přitom o nic záhadného, protože reálné detektory nikdy nemají stoprocentní účinnost, a jejich občasné selhávání je naprosto náhodným statistickým procesem. Proto by mělo být naprosto akceptovatelným postupem, když se do výsledků zahrnou pouze případy, kdy detektory neselhaly, protože se neočekává zlomyslnost typu, že detektor selhává jen v těch případech, které by i tak jen s odřenýma ušima tak tak stihly zachraňovat lokální realismus. Přesto mohli přívrženci lokálního realismu formálně argumentovat, že taková možnost hypoteticky existuje.
Tato mezera byla postupně zacelena s postupujícím zlepšováním účinnosti detektorů. V odpovídajících testech byla ale zase přítomna jiná formální mezera, a to ta, že měření nebylo dostatečně rychlé, takže v principu bylo možné, aby informace z jednoho detektoru došla do druhého rychlostí světla a postarala se o synchronizaci výsledků jich obou. Ani tato varianta nebyla brána zas až tak vážně, protože oddělené části systému byly navzájem dobře izolované - případná synchronizace by tedy musela probíhat prostřednictvím nějaké neznámé interakce, která by nepozorovaně prošla zmíněnými izolacemi, a přitom spolehlivě „našla“ svůj protějšek, se kterým by se následně spikla tak, aby Bellovy nerovnosti vyšly narušené. Tato mezera byla zacelena zase jinými testy, které ale pro změnu zase nedisponovaly dostatečně účinnými detektory.
Výsledky všech těchto předchozích testů ale i tak dost přesvědčivě vypovídaly o narušení Bellových nerovností, a pro přívržence lokálně realistických teorií už zbývalo jenom poslední stéblo naděje, kterého se zoufale chytali. A toto stéblo Ronald Hanson se svým delftským týmem definitivně přetnul jejich experimentem, ve kterém poprvé odstranil obě formální mezery zároveň, tedy jak mezeru působenou nedokonalostí detektorů, tak tu související s požadovanou rychlostí měření.
O delftském experimentu už dostatečně referoval předchozí článek „Kvantová mechanika opět poráží Einsteina a jeho lokální realismus“ od Stanislava Mihulky, nemá proto smysl zde opakovat tam už zmíněné informace, proto zde zmíním jen pár dodatečných detailů. Hanson a spol. použili pro své měření elektrony uvězněné v defektech dvou krystalů diamantu vzdálených od sebe 1,3 km. Protože pro testování Bellových nerovností je nevyhnutelné pracovat s entanglovanými částicemi, tak bylo nutné vzdálené elektrony před zahájením experimentu provázat, což se provedlo s využitím tzv. přenosu entanglementu, kdy se vzdálené částice nejprve provážou s fotony, a tyto fotony se pošlou optickým vláknem na polopropustné zrcadlo, na kterém se pro změnu provážou ony. Dá se ukázat, že tímto způsobem dojde k provázání i původních elektronů úplně stejně dobře, jako by bylo možné je provázat jejich bezprostřední interakcí bez účasti fotonů. V praxi se proto s oblibou používá právě tento způsob přenosu entanglementu, protože entanglement elektronů je záležitost extrémně křehká a při posílání entanglovaných elektronů na jejich vzdálená místa by se s velkou pravděpodobností „rozbil“ (zatímco fotony, jak bylo už zmíněno výše, s tímto problém nemají).
Několik málo mikrosekund po provázání elektronů ve vzdálených krystalech se v tentýž okamžik provede jedno ze zmíněných měření, spočívající ve výběru osy a v následném měření průmětu spinu do této osy. Výběr osy byl svěřen do péče pro ten účel extrémně rychlému generátoru náhodných čísel, který musel umět dostatečně rychle udělat rozhodnutí o tom, která osa se bude měřit (konkrétně musel umět dostatečně rychle vygenerovat náhodné číslo, na jehož základě byl změřen průmět do té které osy). Výsledek tohoto měření byl záznamovým zařízením zaregistrován dříve, než by světlo stihlo dorazit k druhému krystalu, pokud by od prvého krystalu vyrazilo v okamžiku, kdy byla generátorem vybrána měřená osa, díky čemuž byla eliminována hypotetická „rychlostní“ mezera.
Po provedení 245 měření byla získána hodnota výrazu figurujícího v Bellových nerovnostech jako 2,42 se standardní odchylkou 0,2, tedy hodnota dostatečně převyšující maximální hodnotu 2 přípustnou pro lokálně realistické teorie. Tato hodnota je nižší než maximálně přípustná hodnota, kterou povoluje kvantová teorie, a která činí 2,828, kterýžto rozdíl je způsoben jednak ne úplně stoprocentní účinností detektorů (ta se pohybovala kolem 90%), a jednak ne úplně dokonalým entanglementem elektronů (tzv. „přesnost“ – anglicky fidelity – entanglovaného stavu byla 92%).
Delftský experiment tedy definitivně uzavřel více než 80 let starou debatu o podstatě kvantové teorie. Tento experiment neříká, a z principu ani nemůže říct, že kvantová teorie je správnou teorií. Říká ale, že neexistuje žádná alternativní teorie, která by vyhovovala principům lokality a realismu, tak jak požadovali Albert Einstein i mnozí jiní vědci, kteří se nehodlali smířit s podivnými nelokálními korelacemi, které kvantová teorie předpovídá. Tyto nelokální kvantové korelace jsou ve skutečnosti už léta předmětem zkoumání v moderních fyzikálních směrech, jakými jsou výzkum kvantové kryptografie, kvantové teleportace anebo kvantového computingu, ve kterých se rýsuje fascinující potenciál budoucího možného využití především výše zmíněných entanglovaných stavů, ale nejen jich – ale to už by byl zase jiný příběh.
Psáno pro osel.cz
Reference:
Historic Delft Experiments tests Einstein's 'God does not play dice' using quantum 'dice'
Quantum Science and Technology in Diamond
The universe really is weird, and a landmark quantum experiment proves it
EPR paradox
Stern–Gerlach experiment
Spin quantum number
Uncertainty principle
Bohr–Einstein debates
Werner Heisenberg and Albert Einstein
Principle of locality
Bell's theorem
Kvantová mechanika opět poráží Einsteina a jeho lokální realismus
Autor: Stanislav Mihulka (28.10.2015)
Diskuze: