
Jako příklad byla experimentálně studována excitační dynamika substituční nečistoty v sedmi-dimenzionální hyperkubické mřížce. Je dobře známou skutečností, že excitační dynamika lokalizovaných stavů zásadně závisí na dimenzi mřížky, což je dáno základními rozdíly v hustotě stavů na okraji vodivostního pásu. Jeden z klíčových rysů naší techniky je to, že excitační dynamika jakékoli substituční nečistoty v mnohorozměrné mřížce libovolné dimenze se dá exaktně zrealizovat ve vhodné ekvivalentní jednorozměrné (1D) mřížce, kde probíhá identicky, jako v ekvivalentní mnohorozměrné mřížce. Byl předpovězen a experimentálně pozorován vznik ostrého lokalizačního přechodu při kritické vazbě nečistoty. Toto chování je zprostředkováno novým typem vázaného stavu na okraji kontinua, ke kterému dochází u čtyř- nebo vícerozměrných hyperkubických mřížkách, který představuje netriviální doplněk doposud známých vázaných stavů v kontinuu.
Náš článek je výsledkem snažení, které začalo v roce 2014 během mé návštěvy Australie. Není ale prvním, který se zabývá fyzikou v syntetických dimenzích, t.j. dimenzích vyšších, než nám známé tři prostorové dimenze. Tato oblast výzkumu nabývá v posledních 2 - 3 letech, na popularitě a objevila se celá řada zajímavých výsledků. Běžné syntézy vyšších dimenzí obvykle spoléhají na zavedení dalšího parametru a parametrické závislostí Hamiltonianu, nebo na použití uměle vytvořených stupňů volnosti, jako jsou diskrétní frekvence, a pod. Tyto experimenty demonstrovaly syntetické prostory se čtyřmi rozměry. Obecně je cílem dosáhnout dokonalé reprodukce celého multidimenzionálního prostoru. To však nevyhnutelně přináší exponenciálně rostoucí složitost s každou vyšší prostorovou dimenzí.
Náš článek, jehož celý text je volně přístupný na Research Gate, upustil od dosažení dokonalé reprodukce celého multidimenzionálního prostoru. Místo toho jeho cílem bylo věrně reprodukovat okolí jednoho vybraného bodu mnohorozměrné mřížky, včetně excitační dynamiky šířící se z tohoto bodu. V tomto případě libovolná hermitovská mnohorozměrná mřížka s lokální nebo nelokální distribuci vazby mezi jednotlivými body mřížky se da zobrazit na 1D mřížku tak, že lze věrně reprodukovat excitační dynamiku z vybraného bodu mřížky. K vytvořeni vícerozměrného prostředí v ekvivalentní 1D mřížce nepostačuje pouze zachování optického spektra. Místo toho je třeba přesně syntetizovat skutečnou lokální hustotu stavů. Naše metoda nevyžaduje žádnou dynamickou modulaci a přináší obecnou konstrukci zobrazeni na ekvivalentní statické 1D mřížky. Z toho důvodu je kompatibilní s celou řadou stávajících technologických platforem, jako jsou třeba femtosekundovým (fs) laserem psané planární vlnovodné struktury, které byly použity i v našich experimentech. Náš přístup představuje nové obecné paradigma pro selektivní realizaci široké škály užitečných fyzických efektů spojených s mnohorozměrnými mřížkami.
Tato cesta k vyšším dimenzím byla vydlážděna pracemi Lanczose, Paige, a Haydocka počínaje rokem 1950. Tehdy zveřejnil Cornelius Lanczos svůj slavný výsledek, dle kterého libovolná symetrická matice A může být redukována na tridiagonalni matici, což je matice, která má nulové elementy všude, kromě její hlavni diagonály a první diagonály pod a nad hlavní diagonálou. Během studia na vysoké skole se studenti nanejvýš dozvi, že každá normalni (t.j. např. hermitovska) matice A v Hilbertově prostoru, se dá redukovat na diagonální matici (t.j. mající všude nulové elementy kromě její diagonály). Až na permutaci diagonálních elementů je tato diagonální matice jednoznačná. Příslušná báze ve které A je diagonální, je tvořena vlastními vektory A a diagonální elementy A jsou odpovídající vlastní hodnoty A. Na rozdíl od diagonální matice, tridiagonalni matici lze dle Lanczosova algoritmu sestrojit počínaje libovolně zvoleným nenulovým vektorem v0 Hilbertova prostoru, což je samo o sobě pozoruhodný výsledek. Není zapotřebí dodávat, že redukce obecné matice A na tridiagonalni matici, přináší její drastické zjednodušení. Je nutno připomenout, ze Lanczosův algoritmus byl kvůli ztrátě ortogonality v jeho prvních numerických implementacích více než 2 desetiletí do značné míry ignorován, anebo používán s re-ortogonalizací, než v roce 1976 přišel Paige s jeho optimální a stabilní numerickou implementací (tzv. algoritmus A1). Několik let poté, Haydock rozšířil Lanczosuv výsledek na hermitovské matice a aplikoval jej na celou řadu problémů ve fyzice pevných látek.
Žel, základní kurzy lineární algebry pro "nematematiky" doposud opomíjejí tento velmi důležitý a obecný Lanczosův výsledek, který je průsečíkem mnoha směrů v teoretické fyzice a aplikované matematice. Základem Lanczosové konstrukce báze, ve které se daná symetrická matice A stane tridiagonální, a kdy první vektor báze je libovolně zvoleny vektor v0, jsou tříčlenné rekurence, kdy každý další člen posloupnosti je jednoznačně určen předchozími dvěma členy. Jakoby čistou náhodou jsou tyto tříčlenné rekurence identické s nutnými a postačujícími podmínkami, které definuji ortogonální polynomy. Tridiagonálni matice, jako takové, jsou zase známé jako Jacobi matice (neplést s Jacobianem z transformace souřadnic!). Z obecnosti Lanczosove a Haydockovy konstrukce plyne, že systémy ortogonálních polynomů a Jacobi matice jsou všude přítomné a v principu lze každý fyzikální problem redukovat na konstrukci příslušných ortogonálních polynomů. Z obecné vlastnosti ortogonálních polynomu pak plyne, že všechny jejich kořeny jsou jednoduché a tvořeny pouze reálnými čísly.
S rostoucím stupněm polynomu, kořeny polynomu monotonně konverguji k spektru daného fyzikálního problému. Jestli chceme např. získat prvních N úrovní energie na všechny platné číslice v tzv. "double precision", často stačí zvolit polynom stupně N+20 - viz Kvantové modely se spektrem generovaným toky kořenu polynomu. Zdá se, že i studenti fyziky jiných zemí se během svého studia nedozvěděli nic o Lanczosovu výsledku. Jinak by museli hned rozpoznat, že celá řada různých směrů, které vznikly v poslední době, jako jsou (i) Bender-Dunne polynomy v případě kvazi-exaktně řešitelných modelů, (ii) exaktně řešitelné modely, (iii) Schweberovo kvantizační kritérium v Hilbertově prostoru celých analytických funkcí a (iv) diskrétní kvantová mechanika Odakeho a Sasaki, nejsou nic jiného, než realizací Lanczosova-Haydockova rekurzivního řešení - viz. podrobněji v Ann. Phys. 351, 960-974 (2014).
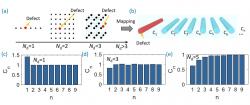
Jakoby těch náhod nebylo dost, vzájemné působení paralelně v jedné rovině probíhajících optických vlnovodů se dá také popsat tříčlennou rekurencí. Takový systém vlnovodu, s předem zvolenou vazbou mezi nejbližšími sousedy, se dá velice přesně experimentálně zrealizovat, resp. napsat fs laserem do skleněné destičky - viz. "femtosecond laser direct‐writing of waveguide circuits in glasses". Průřez takového systému vlnovodu v rovině kolmé k směru šíření vln ve vlnovodech tvoří 1D mřížku. Vzdálenost, kterou vlny ve vlnovodech uběhly, hraje roli času. Excitační dynamiku v takové mřížce lze přímo pozorovat tak, že se do vlnovodu podél její délky přimíchá souvislé množství fluorescenčního materiálu. Když se pak vlna ve vlnovodu šíří, její postup je opticky zviditelněn tím, že každé nové místo, které postupující vlna dosáhne, se rozzáří. Protože dle Lanczosova-Haydockova výsledku lze libovolnou symetrickou, anebo hermitovskou maticí A, redukovat na tridiagonalni matici, a ta je charakterizována specifickou tričlennou rekurencí, tak takovou matici A lze realizovat jako systém paralelně a v jedné rovině probíhajících vlnovodů. Tím se dostáváme k objasnění a pochopeni hlavního experimentálního výsledku našeho článku v Nature Photonics (2019), kterým byla možnost experimentálního studia excitační dynamiky substituční nečistoty v sedmi-dimenzionální hyperkubické mřížce v ekvivalentní 1D mřížce optických vlnovodů.
Co dal?
Nečistoty přestavují lokalizovaný rezonátor. Protože rezonanční vlnová délka rezonátora je velmi citlivá na vnější změny, jsou rezonanční struktury základním prvkem různých typů senzorů. Když pak náhodou objevíte, že třeba nečistota v 20 prostorových dimenzích má výjimečné vlastnosti, nemusíte vzdychat, že je to sice hezké, ale vlastně k ničemu, protože se to nedá experimentálně realizovat. S použitím našeho přístupu dá! Náš článek tímto otevirá a zpřístupňuje nové prostorové dimenze k praktickému využití.
Nebylo to nakonec vše předem zřejmé a přímočaré? Zdá se, že naše pohádky s hleděním do křišťálové koule, nejsou až tak daleko reality, neboť křišťálová koule je již docela blízko naší skleněné destičce. O té křišťálové kouli snad někdy příště.
Literatura
Lukas J. Maczewsky, Kai Wang, Alexander A. Dovgiy, Andrey E. Miroshnichenko, Alexander Moroz, Max Ehrhardt, Matthias Heinrich, Demetrios N. Christodoulides, Alexander Szameit & Andrey A. Sukhorukov.: Synthesizing multi-dimensional excitation dynamics and localization transition in one-dimensional lattices. Nature Photonics 14, 76-81 (2020).
Diskuze:
Blahopřání
Mintaka Earthian,2020-01-04 23:21:44
Hodně energie a kapku štěstí do dalšího zkoumání.
PS:
Těším se na článek o té "křišťálovou kouli".
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce




