K čemu vlastně je rychlá Fourierova transformace
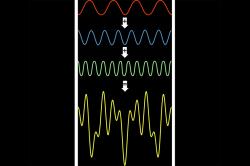
Nejdříve si řekněme, co to vlastně je Fourierova transformace a proč ji potřebujeme. Vysvětlit její princip není úplně jednoduché. Představte si klavír, ten má klávesy, které po stisknutí pohnou kladívkem a to udeří do struny. Každá struna je přesně naladěna na jeden tón, odborně tomu říkáme jednu frekvenci. Jak hráč na klavíru mačká více kláves naráz, vzniká složitá harmonie, skládající se ze zvuků mnoha jednotlivých strun. A Fourierova transformace je matematický aparát, který dokáže tuto harmonii rozložit opět na tóny jednotlivých strun. Jakýkoliv ve své podstatě složitý signál, jako je třeba lidská řeč, hudba nebo výstup z magnetické rezonance je možno popsat jako součet různých frekvencí, právě díky Fourierově transformaci (FT). Odborně se tomu říká, že dostaneme spektrum signálu. Vztáhnuto ke klavírní analogii je spektrum návod, které klávesy a jak silně zmáčknout, abychom z nástroje vyloudili původní zvuk před transformací.
Samotná FT je ale matematicky velice náročná, proto vědci hledali způsob, jak ji zjednodušit, tak aby byl algoritmus pro výpočet co nejrychlejší a přitom zůstala zachována dostatečné přesnost. Výsledkem jejich bádání byl objev Rychlé FT (anglicky Fast Fourier Transformation – FFT). Ta se na začátku šedesátých let minulého století stala základem revoluce ve zpracování signálů, v oblasti zvané signál processing. Dnes ji používáme prakticky ve všech audio vizuálních aplikacích, při kompresi dat a v nespočetné řadě dalších aplikací. Jakákoliv optimalizace výpočetního procesu je tedy vzhledem k ohromnému počtu každodenně vykonávaných operací velkým přínosem.
Pjotr Indyk a Dina Katabi zveřejnili algoritmus, který za určitých podmínek může prováděný výpočet FFT zrychlit stokrát. Zjistili, jak provést výpočet pro omezený počet vzorků signálů a jejich algoritmus se velmi přibližuje teoreticky vypočtenému minimu pro délku algoritmu FFT. To znamená, že dokáží rozložit signál do spektra a poté jej rekonstruovat zpět s dostatečnou přesností, ale potřebují k tomu mnohem méně vzorků a také mnohem kratší výpočetní čas. Oboje je velmi důležité pro následné aplikace.
Jak už bylo řečeno, jednou z oblastí, kde se FFT používá je magnetická rezonance. Nejnže nový algoritmus zkrátí pobyt pacienta v tunelu MRI, ale především umožní vyšetřit větší počet pacientů za stejnou dobu. Idyk svoje snažení zaměřuje především na astronomii. MIT provozuje Haystack Observatory, radioteleskopy, které skládají pomocí interferometrie dohromady jediný obraz s vysokým rozlišením. Zde se jedná opravdu o ohromné objemy dat a velkou výpočetní kapacitu, která je potřeba na jejich zpracování, stejně jako velká disková pole pro uložení posbíraných dat. To vše může nový algoritmus podstatně zredukovat. Uvidíme, jak rychle se nový způsob FFT rozšíří i mezi běžně používané věci, jako je MP3, video, komprimace dat.
Literatura
MIT (Massachusetts Institute of Technology)
FFT na wiki http://cs.wikipedia.org/wiki/Rychl%C3%A1_Fourierova_transformace
Diskuze:
František Luft,2013-12-22 23:58:09
Tak hlavně aby to brzy uměl Matlab. Používám FFT k řešení diferenciálních rovnic na síti. Stonásobné zrychlení by bylo supr :)
MIT má skvělou pověst
Marek Šimon,2013-12-15 12:27:41
MIT má skvělou pověst, ale netušil jsem, že tam mají tak pohledné profesorky. :-)
"pouze za urcitych podminek"
Martin Tůma,2013-12-13 21:19:06
Snazil jsem se to do clanku nejak zabudovat, aby to bylo i pro netechnicky vzdelaneho cloveka pochopitelne. Pro ostatni je tu primo odkaz na puvodni clanek, kde se dozvite podrobnosti :)
Nebyl bych si tak jist
Martin Tůma,2013-12-13 21:17:47
S tim, ze vetsina lidi zde slysela o FFT. Ja jsem se na skole bez ni neobesel, ale je zde rada lidi, kteri nejsou inzenyri elektrotechnickeho smeru. Takovy veterinar, doktor nebo chemik se bez FFT za cele sve vzdelani nemusel potkat vubec.
A já zase jo ;)
Roman Nepšinský,2013-12-18 21:07:33
K té elektrotechnice přidejte minimálně i matematiku a informatiku, předpokládám, že i fyziku atd.
FFT
Jakub Rint,2013-12-13 19:02:56
myslím, že většina čtenářů Osla zrovna o FFT slyšela a velká část i na VŠ.
Stokrát?
Jakub Lédl,2013-12-13 16:48:43
Ten algoritmus má nižší horní mez: pokud je signál délky n k-řídký, pak umožňuje vypočítat DFT v čase O(k log(n)) místo dosavadního O(n log(n)). Nejde o pouhé zlepšení konstantního faktoru, jak popisuje článek.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce