Takzvaná “musica universalis” nebo “hudba sfér” se objevila ve středověku jako filozofická myšlenka spočívající v tom, že na poměry skryté v pohybech nebeských těles – Slunce, Měsíce a planet – by mohlo být pohlíženo jako na formu hudby, sice neslyšitelné, ale dokonale harmonické. Na hudbu (stejně jako na všechno ostatní) se lidé odjakživa snažili uplatňovat geometrická pravidla. Dalším známým příkladem bylo využití tzv. zlatého řezu.

A tak zatímco já jsem jako jedinou geometrii v hudbě dokázal studovat pouze podobnost křivek těla korpulentní harfenistky jejímu nástroji během školního výchovného koncertu, tři profesoři hudby pracující na třech renomovaných univerzitách – Clifton Callender na Florida State University, Ian Quinn na Yale University a Dmitri Tymoczko na Princeton University – vynalezli naprosto nový revoluční způsob matematického rozboru a kategorizace hudby. Jejich metoda získává nevídanou výhodu v rozsahu použití a pomocí komplexní matematické analýzy dokáže vidět hudbu spletenou v dokonalé struktuře, která se dá dokonce vyjádřit pomocí geometrie.

Zvětšit obrázek

První doložená zpráva o snaze vyjádřit hudbu pomocí matematiky pochází od řeckého učence Pythagora z doby téměř půl tisíce let před Kristem.

 
V dubnovém vydání Science vyšla stať, kde toto trio načrtlo metodu nazvanou “geometrická hudební teorie”, která překládá jazyk hudební teorie do současné geometrie. Vzali sekvence not, jakými jsou akordy, takty a stupnice, a kategorizovali je tak, aby mohly být seskupeny do “rodin”. Objevili způsob jak přidělit matematickou strukturu těmto “rodinám”, tak mohou být zastoupeny body v komplexním geometrickém prostoru, podobným způsobem jako je stanovení souřadnic “x” a “y” odpovídající bodům v dvourozměrném prostoru používané v systému středoškolské geometrie. Pro jednoduchou představu, jak to může vypadat, slouží ukázka Chopinova preludia e-moll na rockové fanoušky čeká Smoke on the Water. Kdo chce pochopit více, může si  stáhnout a nainstalovat prográmek Chord geometries 1.1 ze stránky Princetown Music .

Zvětšit obrázek

Obrázek ukazuje jak geometrická hudební teorie ukazuje typy čtyřnotových akordů – soubor not tvoří čtyřstěn s barevnou indikací rozestupů mezi jednotlivými notami v posloupnosti. V modrých oblastech jsou noty seskupené blíže, v teplejších barvách jsou dále od sebe. Červená kulička na špici pyramidy představuje jeden z oblíbených akordů bez jehož existence by nebylo složeno mnoho skladeb v 19. století. Blízko něj jsou všechny nejobvyklejší akordy západní hudby. (Image: Dmitri Tymoczko).

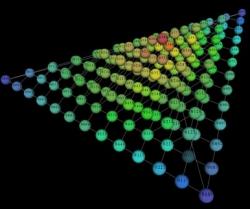
Odlišné typy kategorizace vytvářejí rozdílné geometrické prostory a odráží odlišné způsoby, kterými hudebníci během staletí chápali hudbu. Výzkumníci očekávají, že jim tento úspěch dovolí analyzovat a porozumět hudbě mnohem hlubšími a uspokojivějšími způsoby.
Tato metoda, podle jejích autorů, dovolí analyzovat a porovnat mnoho druhů hudby. (Metoda se zaměřuje na západní styl hudby protože pojem “akord” není univerzální pro všechnu hudbu.) To také začleňuje mnoho dřívějších schémat hudebních teoretiků a směřuje k zachycení hudby v její matematické podobě.

”Hudba sfér není vskutku metaforou – některé hudební prostory jsou skutečnými sférami,” řekl Tymoczko. “Celá otázka tvorby těchto geometrických prostorů je v tom, aby vám nakonec pomohla pochopit hudbu lépe. Silná a efektivní sada prostředků k chápání hudby jako pojmu vám umožní dělat v hudbě všechno, co jste dříve nemohli.”

A co třeba?
”Mohli byste vytvořit nové druhy hudebních nástrojů nebo hudebních hraček,” řekl. “Mohli byste vytvořit nové druhy názorných pomůcek – představte si, že půjdete na koncert vážné hudby, kde bude hudba předložena v obraze. Mohli bychom například změnit i způsob výuky hudebníků. Je tu mnoho praktických aplikací, které by mohly následovat za těmito smělými myšlenkami.”

”Ale pro mě,” dodává Tymoczko, “je nejuspokojivější stránkou tohoto výzkumu, že můžeme jasně vidět, že existuje logická struktura spojující mnoho a mnoho různých hudebních konceptů. Do určité míry můžeme znázornit historii hudby jako dlouhý proces hledání různých symetrií a obecně různých geometrií.”

Dmitri Tymoczko: ”Naše metody nejsou tak dobré, aby rozlišily Aerosmith od Rolling Stones, ale mohly by vám umožnit vizualizovat některé rozdíly například mezi Johnem Lennonem a Paulem McCartneyem. Ale jistě vám pomohou porozumět hlouběji třeba v jakém vztahu je vážná hudba k rocku nebo nakolik je rozdílná.”

Pochopení hudby, jak píší autoři, je procesem vyřazování informací. Dejme tomu, že hudebník hraje “C” na klavír, následované tónem “E” a tónem “G”. Hudebníci mají mnoho různých termínů, jak popsat tuto posloupnost , například “vzestupné C dur arpeggio”, “C dur akord” nebo jednoduše “dur akord”. Autoři poskytují jednotný matematický rámec týkající se těchto rozdílných popisů naprosto stejné hudební události.
Tato trojice popisuje pět odlišných způsobů kategorizace souborů not, které jsou podobné, ale ne identické. Ukazují tyto hudební podoby na jakési “optické symetrii” znázorňující odlišný způsob zanedbávání některých hudebních informací – například toho, ve které oktávě noty jsou, jejich pořadí nebo kolikrát se která nota opakuje. Autoři ukazují, že pět symetrií může být kombinováno vzájemně k vytvoření hojnosti různých hudebních konceptů, z nichž některé jsou důvěrně známé a některé jsou úplně nové.

Tímto způsobem jsou vědci schopní redukovat hudební práce na jejich matematický základ. Noty jsou “přeloženy” do čísel a pak převedeny do jazyka geometrie – výsledkem je bohatá škála geometrických prostorů, z nichž každý je “obydlen” jiným druhem geometrického objektu. Je to jako, když v ZOO různé tvary klecí obývají různé druhy zvířat.

Tato metoda by mohla pomoci zodpovědět otázku, zda existují nové stupnice a akordy, které ještě nebyly objeveny. ”Objevili již západní skladatelé všechny základní a nejdůležitější hudební možnosti?” ptá se Tymoczko. “Pokud ano, pak je západní hudba víc než jen libovolnou skupinou obecných zásad. Může ale být, že základní objekty západní hudby jsou fantasticky detailní, v jejichž případech by mohlo být dost složité objevit alternativy k všeobecným metodám organizace hudby.”

Nástroje pro analýzy také nabízi vzrušující možnost zkoumání rozdílů mezi hudebními styly.

Hudba určitě má svoji logiku a přesnost vpravdě matematickou, ale její působení na lidské emoce je matematickou analýzou nepostižitelné. Zatímco pro mne je Mozartova hudba ztělesněním čehosi dokonalého a podřízeného dokonalému řádu, pro císaře Josefa (pokud bychom měli věřit Formanovu filmu) to bylo jen „příliš mnoho tónů“ a pro moji ženu je to něco na způsob středověkého mučení. A přitom je to stejná hudba, o které bych si já dovolil říci, že je matematicky přesná a v níž každý tón má svoje místo.

Zdroj: Princeton University.