Detekce gravitačních vln byla bezpochyby jedním z největších triumfů fyziky posledních desetiletí. Observatoře jako LIGO a Virgo nám otevřely zcela nové okno do vesmíru, umožňující „poslouchat“ dramatické události, jako jsou srážky černých děr a neutronových hvězd. Jenže, jak už to ve vědě bývá, s každou odpovědí se vynoří deset nových otázek. A jedna z nich zní: co když nám uniká celý orchestr zvuků jen proto, že naše současné nástroje jsou naladěny pouze na hluboké basy?

Současné interferometry jsou totiž skvělé na nízké frekvence, řekněme do 10 kHz, s jistým moderním úsilím dosahujícím až k 300 kHz. To je fajn, ale co ty vysoké frekvence? Co ten kosmický heavy metal v pásmu MHz až GHz? Teoretici nám už nějakou dobu šeptají do ucha, že právě tam by se mohly skrývat signály z raného vesmíru, od exotických kompaktních objektů nebo dokonce stopy fyziky za hranicemi Standardního modelu. Problém je, že chytit takové vlny je asi jako snažit se poslechnout šepot komára uprostřed rockového koncertu – naše současné metody tam ztrácejí citlivost.

Když gravitace ohýbá světlo (ale jinak)

Vědci samozřejmě nespí na vavřínech (i když po některých konferenčních večeřích by si to člověk mohl myslet) a hledají nové cesty. Zkoušely se různé metody, od polarizačních detektorů po zařízení využívající akustické vlny v pevných látkách (BAW) nebo rezonance mezi gravitony a magnony. Hodně nadějí se vkládalo do inverzního Gertsenshteinova jevu – přeměny gravitačních vln na elektromagnetické záření v přítomnosti silného pole. Zní to skvěle, ale zatím buď citlivost nestačí, nebo jsme prostě nic nenašli. Trochu jako hledání klíčů pod lampou, protože tam je lépe vidět, i když jsme je ztratili jinde.

Nyní ale tým z Oxfordské univerzity přichází s něčím, co by mohlo hru změnit. Eduard Atonga a jeho kolegové se podívali na interakci gravitačních a elektromagnetických vln z pohledu vlnové optiky, nikoli jen zjednodušené paprskové optiky, která popisuje třeba klasické interferometry. A objevili něco zajímavého.

Představte si, že světelný paprsek prochází prostředím, kterým zároveň prochází zvuková vlna. Zvuková vlna periodicky mění hustotu (a tedy index lomu) prostředí, což způsobí, že se část světla ohne – rozptýlí do stran pod určitými úhly. Tomu se říká akusto-optický jev a běžně se využívá třeba v laserech.

Atonga a spol. ve své práci, čerstvě publikované na arXiv, ukazují, že něco podobného se děje, když světlo prochází gravitační vlnou. Gravitační vlna sama o sobě je periodická deformace časoprostoru. Tato deformace působí na procházející světlo jako jakási časoprostorová mřížka a způsobuje jeho difrakci – ohyb. Vznikají tak postranní pásma (sidebands) světla s mírně posunutou frekvencí (přesně o frekvenci gravitační vlny) a pod charakteristickými úhly. Nazvali to gravito-optický efekt.

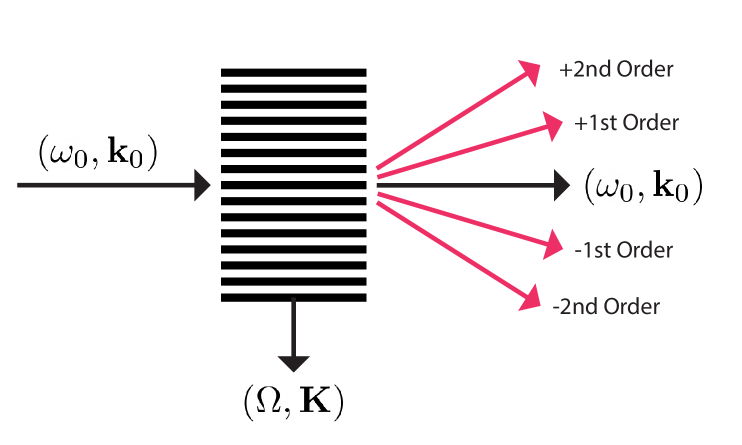
Obrázek 1: Schematické znázornění interakční geometrie. Ukazuje, jak dopadající elektromagnetický svazek (šířící se ve směru x) interaguje s gravitační vlnou (šířící se ve směru z). Ohnuté (difraktované) řády světla jsou vyznačeny červeně. Je to analogie k akusto-optickému jevu, jen místo zvukové vlny je gravitační vlna. Zdroj: Figure 1, Atonga et al. (2025), arXiv:2504.21225v1

Umělecké ztvárnění gravitačních vln deformujících tkáň časoprostoru poblíž futuristického laserového detektoru. Zdroj: Generováno AI.

Jak to změřit? Optická past a chytré počítání

Samotný efekt je samozřejmě extrémně slabý. Gravitační vlny, i ty relativně silné, deformují časoprostor jen nepatrně. Amplituda ohnutého světla a úhel ohybu jsou tak malé, že přímé měření by bylo, řekněme, optimistické. Ale fyzikové jsou vynalézaví. Navrhují použít dva triky:

1. Fabry-Pérotův rezonátor: To je v podstatě past na světlo – dvě vysoce odrazivá zrcadla proti sobě. Světelný paprsek se mezi nimi mnohokrát odrazí, čímž se efektivně prodlouží jeho dráha a zesílí jakákoli interakce, kterou po cestě zažije. V tomto případě interakce s gravitační vlnou. Čím vyšší odrazivost zrcadel (finesa rezonátoru), tím větší zesílení. Dnes umíme vyrobit zrcadla s odrazivostí lepší než 99.9999%, takže finesa může dosahovat miliónů.
2. Heterodynní detekce: Místo abychom se snažili přímo chytit slabounké ohnuté světlo (ty postranní pásma), smícháme ho s původním, neohnutým světlem (nultý difrakční řád). Když se dvě světelné vlny s mírně odlišnou frekvencí smíchají, vznikne zázněj (beat) – signál s frekvencí rovnou rozdílu původních frekvencí. V našem případě je rozdíl frekvencí přesně roven frekvenci gravitační vlny! Tento záznějový signál je mnohem snazší detekovat než samotná postranní pásma.

Kombinací těchto dvou technik vzniká „gravito-optický heterodynní detektor“. Světlo z laseru je vehnáno do Fabry-Pérotova rezonátoru, kterým prochází gravitační vlna. Ta způsobí gravito-optický ohyb, který je v rezonátoru zesílen. Na výstupu se smíchá původní světlo s ohnutým a výsledný záznějový signál se měří.

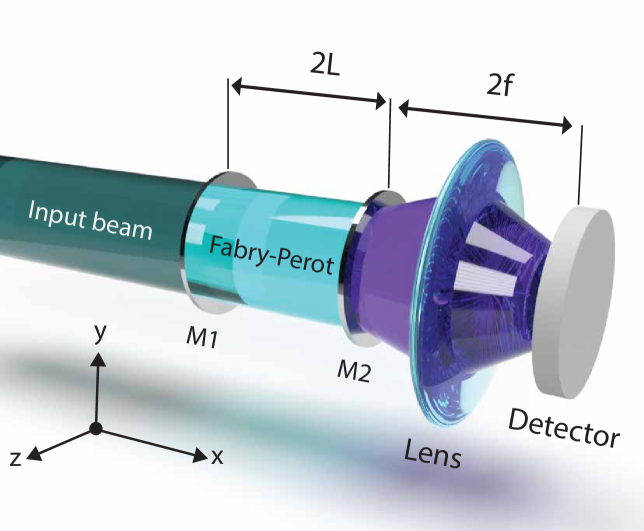
Obrázek 2: Schéma navrhovaného detekčního uspořádání. Laserový svazek vstupuje do Fabry-Pérotova rezonátoru (dvě zrcadla), kterým prochází gravitační vlna (ve směru z). Výstupní světlo je zobrazeno na detektor pomocí systému čoček (2f geometrie). Zdroj: Figure 2, Atonga et al. (2025), arXiv:2504.21225v1

Citlivost a potenciální úlovky

Autoři propočítali očekávanou citlivost takového detektoru pro různé konfigurace – od stolního experimentu (délka rezonátoru 200 m, což tedy úplně stolní není, ale ve srovnání s LIGO...) až po hypotetické detektory dlouhé desítky kilometrů. Výsledky jsou slibné.

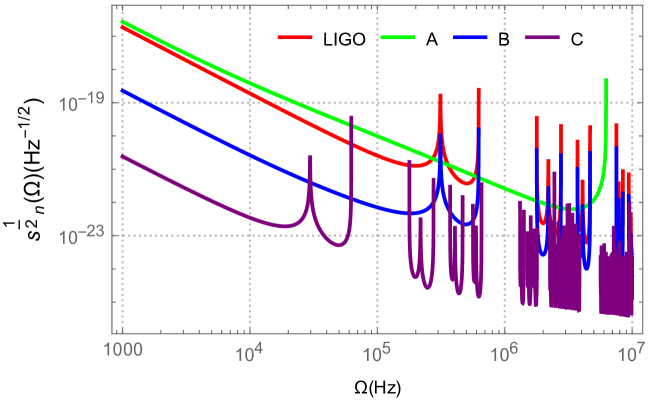
Obrázek 3: Křivky spektrální hustoty šumu pro různé hypotetické detektory (A, B, C podle Tabulky 1 v originální práci, s délkami 200 m, 2 km, 20 km) a pro srovnání s parametry LIGO. Nižší hodnota znamená lepší citlivost. Je vidět, že delší a kvalitnější rezonátory (vyšší finesa) vedou k lepší citlivosti, ale také omezují šířku pásma (rychlé oscilace a pokles citlivosti na vyšších frekvencích). Zdroj: Figure 3, Atonga et al. (2025), arXiv:2504.21225v1

Ukazuje se, že citlivost roste s délkou rezonátoru a jeho finesou (kvalitou zrcadel), ale za cenu užšího frekvenčního pásma, kde je detektor nejcitlivější. To je běžný kompromis. Klíčové ale je, že navržený detektor by mohl být citlivý právě v oblasti MHz-GHz, která je pro současné observatoře nedostupná.

Co bychom tam mohli najít? Jedním z hlavních cílů jsou primordiální černé díry – hypotetické černé díry vzniklé krátce po Velkém třesku, které by mohly mít mnohem menší hmotnosti než ty vznikající kolapsem hvězd. Jejich srážky nebo i samotná jejich existence by mohly generovat vysokofrekvenční gravitační vlny.

Další možností jsou exotické kompaktní objekty, jako jsou bosonové hvězdy nebo gravastary – teoretické alternativy k černým dírám a neutronovým hvězdám, předpovídané některými teoriemi za Standardním modelem. Jejich „zpěv“ by se také mohl ozývat ve vysokých frekvencích.

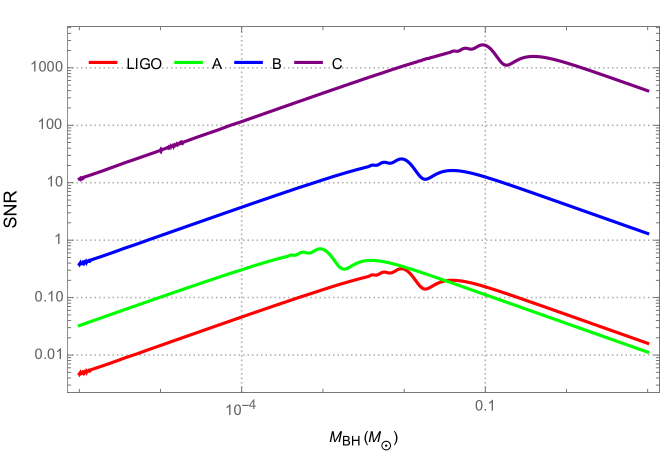
Obrázek 4: Odhadovaný poměr signálu k šumu (SNR) pro detekci transientních signálů (např. ze srážek) pro různé detektory (A, B, C, LIGO) v závislosti na hmotnosti zdroje (MBH) a frekvenci gravitační vlny (Ω). Předpokládá se vzdálenost zdroje 30 kpc (cca střed naší Galaxie). Vyšší SNR znamená snazší detekci. Křivky ukazují potenciál detekovat objekty s hmotností pod hmotností Slunce (sub-solar mass), což by mohlo ukazovat na primordiální černé díry nebo exotické objekty. Zdroj: Figure 4, Atonga et al. (2025), arXiv:2504.21225v1

Dva exotické kompaktní objekty/primordiální černé díry se spirálovitě blíží ke splynutí a vyzařují vysokofrekvenční gravitační vlny. Zdroj: Generováno AI.

Detekce signálu od objektů s hmotností menší než cca 2.6 násobek hmotnosti Slunce (což je odhadovaná spodní hranice pro „běžné“ černé díry vzniklé z hvězd) by byla silným indikátorem nové fyziky. A právě zde by gravito-optický detektor mohl zazářit. Propočty ukazují, že kilometrové detektory by mohly mít dostatečnou citlivost na detekci srážek takovýchto lehkých objektů ve vzdálenosti desítek kiloparseků (tedy v naší Galaxii a jejím okolí).

Budoucnost? Modifikace stávajících detektorů?

Nejzajímavější na celém návrhu je možná to, že technologie potřebná pro stavbu gravito-optického heterodynního detektoru není zas tak odlišná od té, kterou používají současné interferometry jako LIGO nebo plánovaný Cosmic Explorer. Používají lasery, vysoce kvalitní zrcadla, Fabry-Pérotovy rezonátory... Autoři si proto kladou logickou otázku: nemohly by se stávající nebo budoucí observatoře, primárně navržené pro nízké frekvence, upravit tak, aby mohly současně hledat i ve vysokofrekvenčním pásmu pomocí gravito-optického efektu?

To by bylo elegantní řešení – jedním zařízením pokrýt mnohem širší spektrum gravitačních vln. Samozřejmě, ďábel je jako vždy v detailech a bude potřeba další výzkum. Zatím byla analyzována jen nejjednodušší geometrie (kolmý dopad vln). Bude třeba prozkoumat závislost signálu na úhlu a dalších parametrech, aby bylo možné odhadnout reálný počet detekovatelných událostí.

Každopádně, gravito-optický efekt představuje fascinující novou možnost, jak nahlédnout do zatím skrytých zákoutí vesmíru. Možná, že právě díky němu konečně uslyšíme i ty nejvyšší tóny kosmické symfonie. A kdo ví, třeba zjistíme, že vesmír hraje mnohem divočejší hudbu, než jsme si dosud mysleli. A to je přece na vědě to nejlepší – nikdy nevíte, co na vás za dalším rohem (nebo za dalším difrakčním řádem) čeká.

Zdroje a další čtení:

• Atonga, E., Aboushelbaya, R., & Norreys, P. A. (2025). The gravito-optic effect. arXiv:2504.21225v1 [gr-qc]. (https://arxiv.org/abs/2504.21225)
  • Originální preprint studie popisující gravito-optický efekt a navrhovaný detektor. Pro technicky zdatné čtenáře.
• Aggarwal, N., et al. (2021). Challenges and opportunities of gravitational-wave searches at MHz to GHz frequencies. Living Reviews in Relativity, 24(1), 4. (https://link.springer.com/article/10.1007/s41114-021-00032-5)
  • Rozsáhlý přehledový článek o zdrojích a metodách detekce vysokofrekvenčních gravitačních vln. Skvělé pro získání širšího kontextu.
• Ghatak, A. K., & Thyagarajan, K. (1989). Acoustooptlc effect: Raman–Nath diffraction. In Optical Electronics (pp. 508–518). Cambridge University Press.
  • Kapitola v učebnici popisující analogický akusto-optický jev, pokud by vás zajímalo srovnání.
• Maggiore, M. (2007). Gravitational Waves: Volume 1: Theory and Experiments. Oxford University Press.
  • Standardní učebnice o gravitačních vlnách, pokud se chcete ponořit do teorie hlouběji.

Poznámka k termínu „finesa“

Termín „finesa“, použitý v článku, může být méně známý. Jedná se o standardní český technický výraz (přejatý z anglického „finesse“) používaný v optice pro popis kvality Fabry-Pérotova rezonátoru (nebo interferometru). Tato bezrozměrná veličina vyjadřuje, jak „ostrý“ je rezonátor – tedy jak úzké jsou frekvenční rozsahy (rezonanční vrcholy), které rezonátorem projdou nebo jsou v něm zesíleny. Vyšší finesa znamená, že rezonátor je selektivnější pro určité vlnové délky a také že dochází k většímu zesílení intenzity světla uvnitř rezonátoru díky mnoha odrazům mezi zrcadly. Finesa přímo souvisí s odrazivostí zrcadel R a celkovými ztrátami v rezonátoru.

Existuje několik mírně odlišných, ale koncepčně shodných definic finesy. Často se používá $ \mathcal{F} = \frac{\pi \sqrt{R}}{1-R} $. Pro vysoké odrazivosti (R≈1) se často používají aproximace jako $ \mathcal{F} \approx \frac{\pi}{1-R} $ nebo $ \mathcal{F} \approx \frac{2\pi}{1-R^2} $. V původní studii, ze které článek vychází, je v textu (str. 6) naznačena definice $ \mathcal{F}=4R/(1-R) $, zatímco v rovnici (48) popisující finální intenzitu se objevuje výraz odpovídající definici $ \mathcal{F} = 4R/(1-R)^2 $, která lépe odpovídá standardním definicím pro intenzitu. Bez ohledu na přesnou formu definice platí, že čím je odrazivost R blíže jedné, tím je finesa F vyšší.