Na úvod si dejme drobnou rekapitulaci a optimistický výhled na problematiku vesmírného výtahu.
Počátky
Počáteční idea vesmírného výtahu se datuje od 60tých let minulého století. O té doby byla tato myšlenka dále rozvíjena a předkládána veřejnosti jako například v díle Atrhura C. Clarke – Rajské fontány (1979), formou mnoha knižních derivátů, televizních děl a několika počítačových her. Nechme nyní beletrii a zábavní tvorbu poněkud stranou a pojďme se podívat jak na realitu vesmírného výtahu pohlíží svět fyziky.
Umístění výtahu v gravitačním poli Země
Umístěme počátek souřadného systému do středu Země a nechme ho rotovat rychlostí jedné otáčky za den, pak následující rovnice popisuje zrychlení pro vybraný statický bod nacházející se v rovině řezu Zemí v rovníku:
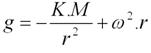
Kde:
g je zrychlení podél poloměru (m.s-2),
K je gravitační konstanta (m3.s-2.kg-1.)
M je hmotnost Země (kg)
r je vzdálenost od tohoto bodu do středu Země (m),
ω je rychlost rotace Země (y-2).
Zrychlení na Zemském povrchu vypočítáme následovně:
![]()
a po úpravě dostáváme
.
![]()
V určitém bodě nad rovníkem se pak odstředivá a gravitační síla ruší a dostáváme geosynchroní trajektorii ve výšce 42,164 km (měřeno od středu Země).
![]()
nebo po dosazení
.
![]()
Z tohoto nám vychází, že část lana pod geostacionární stanicí bude urychlována směrem k Zemi a lano nad ní bude urychlováno směrem do vesmíru. Pokud by bylo lano spuštěno dolů k Zemi, pak musí být samozřejmě správně vyváženo na stranu od Země. Jakmile by došlo k ukotvení volného konce lana k Zemi posunutím zátěže dále od centra rovnováhy, dosáhli bychom jeho napnutí. Toto lano by pak mohlo být použito jako výtah.
Teorie nosného lana
Hlavním technickým problémem takového lana vyrobeného z současně dostupných materiálů a majícího stejný průměr po celé své délce je, že by se přetrhlo vlastní vahou. Řešením je následující differenciální rovnice:
σ*dS = g*ρ*S*dr
g je zrychlení podél poloměru (m.s-2)
S je plocha kabelu v jakémkoliv bodě r (m2) dS a jeho variace (m2)
ρ je hustota materiálu použitého pro kabel (kg.m-3)
σ je mez pružnosti materiálu (Nm-2 = kg.m-1.s-2)
Tato rovnice říká, že v každém bodě lana musí být násobek meze pružnosti s danou plochou roven aktuálnímu gravitačnímu zrychlení působícím na hmotu lana.
Po dosazení za g z původní rovnice dostaneme následující (pro vzdálenost z povrchu Země na geostacionární dráhu):
![]()
a další úpravě:
![]()
kde x = ω2*r0 / g0
je poměr mezi odstředivou silou působící na rovníku a silou gravitační. Z těchto dvou rovnic je patrný zásadní vliv poměru g0*r0, tedy poloměru Země a gravitačního zrychlení na průměr lana. Dalším poznatkem je vliv odstředivé síly vyvolané rotací Země ve výsledku snižující nároky na pevnost lana přibližně o jednu třetinu.
Materiál Lana
Druhým technickým problémem je, že nároky na materiál lana dané součinitelem g0*r0 jsou jednoduše příliš velké. Námáhání lana roste s jeho délkou v gravitačním poli exponenciálně. Na úrovni Zemského povrchu pak máme:
g0.r0 = 62,5 106 m2.s-2 (nebo J / kg)
ρ = 5 103 pro většinu pevných látek, takže požadovaná mez pružnosti materiálu σ je například:
σ ~ 300 109 kg.m-1.s-2.
To odpovídá kabelu z materiálu schopného při průřezu jednoho čtverečního milimetru unést v gravitačním poli Země (ve výšce 0m n.m.) náklad o váze 30 t.
Jakou nosnost tedy musí mít lano pro vesmírný výtah?
Na předchozích rovnicích jsme si ukázali, že nosnost lana není jediným parametrem vstupujícím do hry. Pokud by bylo takové lano konstruováno z oceli, tak by v místě vyrovnání gravitační a odstředivé síly mělo průřez asi poloviny Zemského průřezu na rovníku. Pro zjednodušení popisu potřebného materiálu vědci zavádí jednotku zvanou Yuri – specifickou nosnost materiálu. O jednotce Yuri jsem se již zmínil v článku Výsledky vesmírných výtahových her pro rok 2009, připomeňme si že tato jednotka je poměrem pevnosti v tahu vůči své hmotnosti:
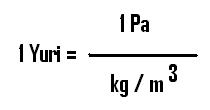
Z předchozích rovnic nám pak vychází, že by stavba výtahu byla reálná s materiálem o hodnotách 40-50 Yuri (např. mez pružnosti 88-110 GPa, při podélné hustotě 2 g/m). Uváděná hodnota je již včetně bezpečnostních koeficientů a částečně zohledňuje i další vstupní parametry jako je výkon zdviže, návratnost projektu, jeho obslužnost a jiné, které si rozebereme příště. Prozatím berme toto číslo jako jakousi optimální hodnotu, která nám umožní se dostat k možným návrhovým číslům.
Udělejme si odbočku do Japonska k fyzikovi Sumio Iijima, jehož objev poprvé rozvířil diskusi nad možností přepravy materiálu vesmírným výtahem na oběžnou dráhu Země. Pan Sumio Iijima totiž počátkem 90tých let minulého století publikoval vědeckou práci na téma uhlíkových nanotrubiček (Carbon Nano Tubes – CNT), na jejímž základě se myšlenka vesmírného výtahu posunula ze stránek beletrie na rýsovací prkna inženýrů.
Uhlíkové nanotrubičky (Carbon Nano Tubes – CNT)
Úvodní výpočty a počítačové simulace naznačovali že nanotrubičky by měli vydržet až 50 GPa (22 Yuri) v tahu, což bylo následně potvrzeno i experimentálně. Další prostorové configurace CNT by měli teoreticky dosahovat pevnosti 126 GPa (57 Yuri) a poslední výzkumy zatím končí vícestěnnými CNT (MWNT) a jejich teoretickou pevností až 150 GPa (68 Yuri).
Vraťme se zpět k problematice vesmírnému výtahu. CNT by nám podle výpočtů a simulací měly poskytnout pevnost v tahu až 68 Yuri (150 GPa). V předešlých odstavcích jsme si také ukázali, že požadavky na stavbu se pohybují mezi 40-50 Yuri. Teď si položme otázku, proč tedy vesmírný výtah za uplynulých 20 let nebyl nepostaven, nebo se o jeho konstrukci alespoň někdo nepokusil?
Co se z počátku zdálo jako být jasnou záležitostí se totiž posléze začalo zásadně komplikovat. Prvním problémem bylo vytvořit uhlíkové nanotrubičky dosahující délky vyšší několika milimetrů. O několik let později se k tomuto problému přidává vysoká náchylnost CNT k narušení stěn a to jak při výrobě, tak při namáhání samém. Důsledkem je snížení nosnosti o závratných 75 %. Pokud teď vezmeme vypočtenou specifickou nosnost vícestěnných CNT (68Yuri) a odečteme zmiňovaných 75 % dostáváme hodnotu 17 Yuri, která je výrazně nižší než potřebných 40 Yuri.
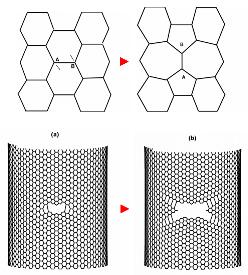
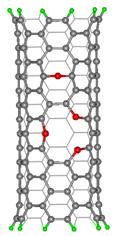
Porušená stěna CTN a šíření “oka”.
Nyní si opět položme otázku, proč tu již není vesmírný výtah? Odpověď by teď měla být poměrně jednoduchá a od dob A. C. Clarka se ani moc nezměnila. V současnosti nedisponujeme známým materiálem, který by mohl být použit na konstrukci výtahového lana. Problémem je, že naděje vkládané do uhlíkových nanotrubiček byly prozatím liché a zatím neznáme jiný materiál s vhodnějšími vlastnostmi. Nejdelší vytvořená nanotrubička se nyní stále měří spíše v milimetrech než požadovaných stovkách kilometrů a problémy s narušením jejich stěn se zatím nedaří řešit. Dalším problémem je absence potřeby materiálu těchto parametrů v běžné průmyslové výrobě, kromě teoretické potřeby vesmírného výtahu, což omezuje přirozené investice do výzkumu v tomto oboru. Jediným motivátorem je NASA pořádající vesmírné výtahové hry, ale i přes štědrou odměnu se soutěžící do této disciplíny nehrnou. Můžeme jen doufat, že v budoucnu dojde k technologickému pokroku, který nám konstrukci výtahu umožní. V současnosti však tato stavba reálná není.

Soutěžní páska Japonského týmu z Vesmírných výtahových her pro rok 2008, po testu.
Abychom nekončili příliš depresivní nótou, tak předesílám, že si v příštím díle rozebereme uvažované možnosti napájení zdviže, problémy vibrace lana způsobené jeho ukotvením i atmosférickými vlivy a pravděpodobnost kolize s odpadem na oběžné dráze. Ač se tyto problémy mohou zdát zásadní, tak jejich navrhovaná řešení jsou technicky velmi zajímavá a dávají šanci na úspěch.
Další příklady poruch ve stěnách CNT:
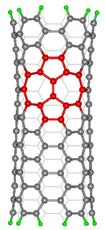
Porucha nazývaná “kamenná zeď”
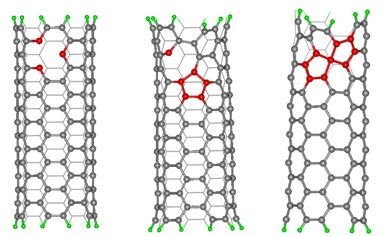
Další možné poruchy stability ve stěně.
Porucha nazývaná “Přeskupení atomu“

Trocha humoru z kuchyně „vesmírného výtahu“ (ref. http://www.imdb.com/title/tt0468999/).
V reakci na komentáře uvedené pod článkem bych chtěl uvést následující upřesnění a doplnění:
V odstavci "Teorie nosného lana" - differenciální rovnice σ*dS = g*ρ*S*dr - řeší podmínku sigma=konst., právě přechodem k profilaci jeho průřezu S po dělce lana. SIGMA v diferenciální rovnici pro délkový element není mez pružnosti, nýbrž je to mezní přípustné napětí v tahu. Tato rovnice říká, že každý úsek lana něco váží a tak mu k jeho průřezu na jeho horním konci přidáme i přírůstek průřezu právě tak velký, aby pokryl tíhu toho úseku. Tím nám bude průřez s výškou růst, alespoň tedy až do místa, kde se otočí znaménko zrychlení (na té geostacionární orbitě). A za cenu růstu průřezu se umožní to, aby se napětí materiálu udržovalo na nějaké vhodné velikosti, nejlépe konstantní a rovné přípustnému maximu (se zahrnutím nějaké bezpečnosti). To je cesta k efektivnímu využití materiálu (Jiří Zbytovský).
Detailně je výpočet uveden na http://www.zadar.net/space-elevator/ (Petr K).
Zdroje:
http://www.spaceelevatorblog.com
http://www.spaceelevatorgames.org
http://www.lasermotive.com/blog/?p=489
http://cosmiclog.msnbc.msn.com/archive/2009/08/17/2033079.aspx
http://www.spaceward.org/documents/papers/The%20Space%20Elevator%20Feasibility%20Condition.pdf
http://io9.com/5206012/this-space-elevator-is-the-terrorists-next-target
http://www.pcworld.com/article/170199/space_elevator_science_fiction_or_global_warming_cure.html
http://www.redorbit.com/news/space/1563762/japan_looking_to_build_worlds_first_space_elevator/
http://en.wikipedia.org/wiki/Carbon_nanotube#Defects
http://fy.chalmers.se/OLDUSERS/fengding/CNTs.htm
http://en.wikipedia.org/wiki/Space_elevator
Diskuze:
Hodinky
Milan Vondráček,2010-02-02 23:28:25
Tak to se mi ten výtah vůbec nelíbí. Jestli ho postaví a začnou po něm nahoru tahat náklady, budu si muset častěji seřizovat hodinky. Urychlování stoupajícího nákladu jde (jak bylo správně popsáno jinde) na úkor zpomalování rotace Země. Už teď chudinka zpomaluje kvůli slapovým silám o sekundu každých pár desítek tisíc let a teď tohle!
Bouře
Jiří Zbytovský,2010-02-01 15:22:50
sorry za dvojáka. Navíc to patřilo pod "Jiří Pospíšil" Ještě mě udivilo tvrzení v článku ohledně bouřek. Nechce se mi věřit, že by existovalo na rovníku na moři místo, kde by se nevyskytovaly bouřky. Také se mi nezdá býti možným nějak plošinou manévrovat pro případné vyhnutí se bouři. Vývoj bouřkové buňky od počátku příznaků do plné síly trvá pouhé desítky minut a rychlost šíření klidně desítky km/h. Takové manévrovací možnosti těžko bude mít plovoucí základna velikosti vrtné plošiny.
Tak
Jiří Zbytovský,2010-02-01 15:13:40
ta reakce lana na boční sílu nákladu není zas příliš složitá. Předpokládejme, že rychlost nákladu bude mnohem menší, než rychlost vln na laně, to bude řekl bych že dobře splněno, pak se to bude řešit jako napnutá tětiva a jde o reakci toho koncového závaží:
Stoupání nákladu napne tětivu proti směru rotace země.
Tím se tah lana u závaží mírně vyosí tak, že se orbitální rychlost závaží bude mírně brzdit.
Radiální složka tahu lana zůstane zatím prakticky beze změny.
Po nějaké době působení se naintegruje rozdílová rychlost, s jakou závaží zaostává za rychlostí orbitální a následně i rozdílová vzdálenost. Celé lano se tím nahne tak, že přestane vést od země kolmo (malá část této úhlové odchylky vznikla již přímo působením nákladu do tětivy, nyní to bude hlavně od změny polohy konce lana.
V důsledku náklonu lana se o něco sníží orbita závaží a zmenší jeho tah u paty. Pokud je co snižovat (je dost velká rezerva toho tahu v klidu, tak se to ustálí na tomto menším tahu a výkyv lana se už dále nebude zvyšovat. V opačném případě by možná mohlo dojít ke ztrátě stability lana. Nyní máme teda novou silovou konfiguraci, také stabilní a vlivem malých náklonů lana vůči kolmici dochází k přenosu oněch sil, o které nám jde - rotace Země se brzdí a náklad se bočně urychluje. Po dopravení nákladu se to závaží zase vrátí zpátky, protože po odlehčení nákladu ho bude Země urychlovat jako náklad, zjednodušeně řečeno. Je to trošku, neřekl bych složité, ale náročnější na přesnost v představivosti a určení co s čím souvisí. Pokud Vám to nepude, tak si z toho nic nedělejte, můžete i tak bez obav věřit tomu, že odborníci na věc (a to ani já rozhodně nejsem) ví o čem mluví a mají to vyjasněné a celá věc není jen nějaká hámotina.
Jo a drobnost - lano samozřejmě nemusí být na rovníku, nic v zásadě nebrání tomu, aby končilo na nějaké jiné zeměpisné šířce, samozřejmě ne na pólu, to by se nemohly zachycovat ty boční síly, ani v blízké oblasti pólu, to by se tam plouhalo po zemi. Ale na vlastním území řekněme USA by to mohlo klidně být. Bude to sice trochu prověšené, ale myslím si, že menší praktické těžkosti budou v případě, že si to Amíci postaví (kdo jinej?) na vlastním, než když se budou muset handrkovat s nějakými hotentoty z mezinárodních společenstev o kompetence a povolení.
Tak
Jiří Zbytovský,2010-02-01 15:13:09
ta reakce lana na boční sílu nákladu není zas příliš složitá. Předpokládejme, že rychlost nákladu bude mnohem menší, než rychlost vln na laně, to bude řekl bych že dobře splněno, pak se to bude řešit jako napnutá tětiva a jde o reakci toho koncového závaží:
Stoupání nákladu napne tětivu proti směru rotace země.
Tím se tah lana u závaží mírně vyosí tak, že se orbitální rychlost závaží bude mírně brzdit.
Radiální složka tahu lana zůstane zatím prakticky beze změny.
Po nějaké době působení se naintegruje rozdílová rychlost, s jakou závaží zaostává za rychlostí orbitální a následně i rozdílová vzdálenost. Celé lano se tím nahne tak, že přestane vést od země kolmo (malá část této úhlové odchylky vznikla již přímo působením nákladu do tětivy, nyní to bude hlavně od změny polohy konce lana.
V důsledku náklonu lana se o něco sníží orbita závaží a zmenší jeho tah u paty. Pokud je co snižovat (je dost velká rezerva toho tahu v klidu, tak se to ustálí na tomto menším tahu a výkyv lana se už dále nebude zvyšovat. V opačném případě by možná mohlo dojít ke ztrátě stability lana. Nyní máme teda novou silovou konfiguraci, také stabilní a vlivem malých náklonů lana vůči kolmici dochází k přenosu oněch sil, o které nám jde - rotace Země se brzdí a náklad se bočně urychluje. Po dopravení nákladu se to závaží zase vrátí zpátky, protože po odlehčení nákladu ho bude Země urychlovat jako náklad, zjednodušeně řečeno. Je to trošku, neřekl bych složité, ale náročnější na přesnost v představivosti a určení co s čím souvisí. Pokud Vám to nepude, tak si z toho nic nedělejte, můžete i tak bez obav věřit tomu, že odborníci na věc (a to ani já rozhodně nejsem) ví o čem mluví a mají to vyjasněné a celá věc není jen nějaká hámotina.
Jo a drobnost - lano samozřejmě nemusí být na rovníku, nic v zásadě nebrání tomu, aby končilo na nějaké jiné zeměpisné šířce, samozřejmě ne na pólu, to by se nemohly zachycovat ty boční síly, ani v blízké oblasti pólu, to by se tam plouhalo po zemi. Ale na vlastním území řekněme USA by to mohlo klidně být. Bude to sice trochu prověšené, ale myslím si, že menší praktické těžkosti budou v případě, že si to Amíci postaví (kdo jinej?) na vlastním, než když se budou muset handrkovat s nějakými hotentoty z mezinárodních společenstev o kompetence a povolení.
Pekny link
Petr K,2010-02-01 11:00:26
http://www.zadar.net/space-elevator/
je to tam docela zevrubne vysvetleno, vcetne spousty vypoctu.
To fakt není možné s některými z vás.
Jiří Pospíšil,2010-01-31 20:04:30
Ano, Coriolisova síla působí jen na tělesa, která se po zemském povrchu pohybují od rovníku nebo k rovníku. A to právě proto, že se tímto pohybem jejich vzdálenost ve vztahu k ose otáčení mění a tím se při jejich stále rychlosti mění jejich úhlová rychlost, tedy ve vztahu k otáčení zrychluje, když jedou od rovníku a zpomaluje, když jedou k rovníku. Na rovníku nepůsobí, protože se vzdálenost ve vztahu k ose otáčení země mění jen nepatrně. Nepůsobí také nikde tam, kde se náklady posouvají ve směru poledníků.
Já myslel, že se bavíme o výtahu, který se zvedáním předmětů se bude vzdalovat od osy otáčení a bude tedy ve vztahu k povrchu země zpomalován a při klesání bude zrychlován. Jinde než na rovníku tento výtah ani být nemůže. A bude ta Coriolisova síla právě tam působit naplno, Protože jiný pohyb než nahoru a dolů tam z hlediska povrchu země být ani nesmí. Vzdálí-li se od země o jeden poloměr země, musí aby z hlediska pozorovatele byl stále ještě nad ním, zrychlit z nuly na obvod země děleno časem otáčky země. Ve skutečnosti bude mít tuto rychlost dvakrát, ale jednou ji měl už na povrchu, tak jako vše, co se na rovníku nehýbe. A tuto změnu z 1667 km/hod na 3333 km/hod musí něco nákladu dodat.
Zapomeňte na to, že právě to se jmenuje Coriolisova sila, a řešte ten problem. Zvedat deka nemá cenu, náklady budou v tunách. A ty tuny musíte urychlit, jinak vám nad hlavou prostě nezůstanou. A aby vám to neodtáhlo protizávaží z místa, tak buď musí mít obrovskou hmotnost, nebo ho tam musíte držet silami daleko většími, protože si ty vektory prostě nakreslete a uvidíte. Obrovskou silou budete táhnout protizávaží k zemi, tím se bude relativně předbíhat. Protože má daleko větší rychlost, aby při vzálenosti bylo stále nad hlavou vypouštěče. Tak se při přiblížení předběhne.
Představa protizávaží, pohybujícího se tak, aby se lano udrželo stále nad hlavou, v otáčející se soustavě je docela srandovní, i když ho rozložíte na nějaké proti závažíčka. Čím jich budete mít více, tím srandovnější výpočty. A připočtěte kmity, které při napětí bude mít lano tendenci vytvářet a po chvíli se zasmějete a necháte toho.
Tohle bude dražší než tam poslat raketu se stejným nákladem.
Já bych takové věci pro začátek zkoušel mezi kontinenty. Třeba by po takovém laně mohly lodi ručkovat mezi kontinenty, když je to lano tak bezva. Nebo udělat silnice bez předjíždění, že by se auta jako zahákly do oka na laně a nechaly by se táhnout. Zdejší perpetumobilisti mohou vymyslet, jak se uspoří tím, že se vzájemně zruší síly, když jedny auta pojedou tam, a druhá zpátky.
kdo rika, ze se ta stanice ani nehne?
Ondra Habarcik,2010-02-01 11:29:28
Myslim, ze vsichni souhlasi s tim, ze se to cele rozkmita, tedy i stanice a vysledkem bude neco jako kyvadlo. Nekde se ta energie na uhlove urychleni vytahu musi vzit, ale rozhodne nepujde cela na ukor stanice, min. polovina pujde na ukor Zeme (jestli predpokladate vliv na stanici, potom tohle musite prijmout), casem by se mela na ukor Zeme postupne temer uplne cela vstrebat pres to lano, jeho napinani.
re: Jak na to tak koukám..
Jan Bilek,2010-01-30 22:08:18
Zdravím pane Zbytovský,
děkuji za podnětný komentář. Přiznávám se, že jsem čerpal z několika zdrojů a snažil se je mezi sebou kombinovat tak aby celek vypadal celistvě. Současně jsem se snažil vybalancovat obtížnost a pochopitelnost na rozumné úrovni a nakonec jsem bojoval s názvoslovím (mez pružnosti x mezní přípustné napětí v tahu), překladem ze zdrojů. Současně přiznávám že Váš popis rovnic je lepší, osobně jsem měl pocit nedostatečnosti už při psaní, ale prostě jsem to lépe nedokázal. Nyní se snažím dát dokupy další článek s obsahem jenž jsem uvedl a současně bych chtěl dát prostor k odpovědím na otázky položené v diskusi. Myslím si že by bylo i záhodno uvést na pravou míru místa, která jste vytknul. Vaší pomoci při tvorbě článku bych si velmi vážil a cenil bych si Vaší pomoci. Můžete mě prosím v případě zájmu o spolupráci kontaktovat?
Jak na to tak koukám..
Jiří Zbytovský,2010-01-30 19:34:33
V odstavci "Teorie nosného lana" je několik chyb.
-před větou "Řešením je následující differenciální rovnice:"
chybí informace, co tato rovnice řeší - že to je oproti konstantnímu průřezu v předchozí větě právě přechod k profilaci jeho průřezu S tak, aby byla splněna podmínka sigma=konst. Bez tohoto vysvětlení je to to matoucí.
-dále a především SIGMA v diferenciální rovnici pro délkový element není mez pružnosti, nýbrž je to mezní přípustné napětí v tahu. Tato záměna se ještě opakuje v další větě. Protože vlastní rovnice i rozměry v popisu jsou správně, dělá to na mě dojem jako chyba překladu. Pane Bílku, odkud jste to takhle neobratně vopsal? Vždyť vůbec nevíte, co píšete :-)
-hned následující věta: "Tato rovnice říká, že v každém bodě lana musí být násobek meze pružnosti s danou plochou roven aktuálnímu gravitačnímu zrychlení působícím na hmotu lana."...je taky úplně špatně a to i když si opravím termín "mez pružnosti" na napětí.
Tato rovnice říká že nikoli násobek sigma s plochou, ale násobek dé-sigma, čili přírůstku průřezu se něčemu rovná. A nerovná se jen aktuálnímu zrychlení, ale tíze toho délkového elementu lana v daném zrychlení.
Jinak a lidsky - jde o to, že každý úsek lana něco váží a tak mu k jeho průřezu na jeho horním konci přidáme i přírůstek průřezu právě tak velký, aby pokryl tíhu toho úseku. Tím nám bude průřez s výškou růst, alespoň tedy až do místa, kde se otočí znaménko zrychlení, to je na té geost. orbitě. A za cenu růstu průřezu se umožní to, aby se napětí materiálu udržovalo na nějaké vhodné velikosti, nejlépe konstantní a rovné přípustnému maximu (se zahrnutím nějaké bezpečnosti - počítat to na mez pevnosti by nebylo moc šikovné) To je cesta k efektivnímu využití materiálu. No a když přejdeme k infinitezimálním přírůstkům, dostanem tu dif. rovnici, jejímž řešením je přímo funkce Sr(S0,r,ro,sigma,atd), která udává velikosti průřezu jako funkci, ve které vystupují jako proměnné: výška r, zrychlení a(r), průřez lana u paty S0, hustota ro a ta pevnost sigma.
Ten výpočet není uveden, škoda, pokud se k tomu dokopu, tak ho sem možná postnu sám. Kdysi jsem si to spočítal, tak bych to mohl dát dokupy:-) Ale nic neslibuju!
Ta funkce vypadá nějak tak, že poměr Sr/So se rovná exponenciále a ta má v exponentu: poměr ro/sigma a ten se násobí závorkou s několika členy různých mocnin r, které vznikly integrací složek zrychlení a rozepsáním při dosazení za meze určitého integrálu. A + nějaké ty konstanty. Důležité je to, že sigma a ro tam vystupují jen ve vzájemném podílu, což je vlastně ta veličina YURI, a pak si musíme uvědomit, že když výchozí podmínka je sigma=konst, tak se na koncích lana musí splnit jako okrajová podmínka zachycení odpovídajících sil, čili dole bude to lano ukotvené a napjaté silou, které odpovídá sigma*S0 a podobně na jeho horním konci ho musíme ukotvit k nějakému závaží.
Ještě k reakci lana na zatížení. K problematice bočních sil se níže vyjádřil - dle mého věcně zcela správně, stručně a jasně Stanislav Brabec (Korekce setrvačné síly 27.01.2010 v 10:41). Nemám k tomu co dodat.
Ke svislé reakci lana na zátěž: Je nutno si uvědomit, že když na lano něco dole pověsím, např metr nad jeho ukotvením, tak se zatížení lana tíhou zátěže se nezpůsobí vzrůst napětí v laně nad zátěží, ale o přidanou sílu se ZMENŠÍ tah lana POD zátěží a jdoucí do ukotvení. To platí samozřejmě jen pokud dodržíme podmínku, že zátěž je menší, než tah v ukotvení. Kdybychom to přehnali, tak bychom to lano začli stahovat dolů. Pokud ne a úsek pod zátěží zůstane aspoň trochu napjatý, tak se zatížený bod sníží jen o součin tuhosti spodního úseku a tíhy nákladu. To jsou reálně nějaká ta promile délky, na metru nějaký milimetr. Tuhost horního úseku se prakticky neuplatní, protože je kvůli velké zúčastněné délce moc malá. Jak bude náklad stoupat, bude časem klesat jeho tíha a tím se bude napětí pod ním postupně vracet k původní hodnotě - a my můžem po čase poslat nahoru další náklad. K problému stahování lana vlivem zátěže tedy nedojde. Snad vše (prozatím)
Omluvte pls délku příspěvku, já to stručně nějak neumim :-)
Ještě jinak
Xavier Vomáčka,2010-01-29 17:17:17
Pokud připevním na okraj setrvačníku tyč tak, že tyč bude v rovině setrvačníku a osa tyče bude protínat osu setrvačníku, tak ta tyč mimo to, že posune setrvačníku těžiště mimo původní osu otáčení, nebude na setrvačník působit žádnou silou (jedině pokud bude původní osa setrvačníku pevně uchycena, potom to bude "házet", ale zase jen "odstředivě" od osy otáčení). Žádná boční síla se neprojeví.
Coriolisova síla
Xavier Vomáčka,2010-01-29 15:28:42
Coriolisova síla je vektor tvořený vektorovým součinem mezi vektorem ve směru pohybu tělesa (v neinerciální soustavě) a vektoru směru rotace (Země) v tom daném bodě. Když si to představím, tam na rovníku při pohybu po svislici žádná Coriolisova síla na těleso přece nepůsobí! Naopak pokud by se těleso pohybovalo po tečně ve směru sever jih, tak by síla byla maximální.
Nebo si to pletu?
Ondro Habarčíku,
Jiří Pospíšil,2010-01-28 14:23:31
když nevíte, co to Coriolisovy síly jsou, tak jinak. Tento výtah je představitelný jen na rovníku. S tím asi souhlasíte. Na to, aby zvedaný předmět mohl zůstavat na laně a lano nedeformoval, je třeba, aby měl stejnou úhlovou rychlost, jako otáčející se země. S tím asi taky souhlasíte. Z toho vyplývá, že aby řekněme desetitunový náklad byl zvednut do vzdálenosti řekněme poloměru země, musí být urychlen nějakou silou, která těm deseti tunám přidá boční rychlost 40000/24 km/hod. Jinak vám bude soustavu táhnout dozadu a namotávat na zemi s postupným zrychlováním relativně rychlého nárazu protizávaží do země. Jistě jste již viděl, jak se lano namotává na tyč, když má na konci kouli a původně obíhalo tu tyč. Boční síla bude potřebná taková, aby při dané rychlosti vzestupu zůstávala úhlová rychlost beze změny. Spoléhat se na tah v laně nejde, protože tahové síly jsou k této boční síle kolmé, při délce lana prakticky absolutně. Vyrovnávání v jiných místech protizávažími klesajícími nebude mít valný smysl vzhledem k boční nestabilitě (tuhosti) této soustavy. A vytvoří jen další deformaci lana do boku. Následné kmity mohou vést k velmi zajímavým katastrofám.
Problémy se stavbou. Lano nejde postavit odspodu. Ledaže by ho někdo natahoval, pak ovšem nesmí mit boční tuhost skoro žádnou, že jo. Jinak by ho neodmotal z té kabelové špůlky. Vytahovat od niti to taky nepůjde, protože to by hmotnost konečnou jen zvyšovalo. Smotávat ho z na montážní stoupající plošině z nanotrubiček tam vyrobených, zadává problémy ještě problematičtější, než nás napadly dosud. Spouštět shora to taky nejde, protože tam by se to natahovalo od země, s tou představou, že to bude napínáno odstředivou silou. Mimoto by tam někdo musel nějak dopravit ty nanotrubičky, motač lana a směřovač lana. To taky není možné bez energie. A bez přísunu materiálů, a to bez použití výtahu. Ten se teprve staví.
Já už s tou debatou o novém druhu perpetua mobile končím.
Na dopravu čehokoli ve vesmíru kamkoli spotřebujete stejně energie, ať to tam dopravujete jak chcete. A to nepočítám tu energii, kterou vyplýtváte navíc na stavbu páternoster monster.
Coriolisova sila?
Ondra Habarcik,2010-01-27 10:13:42
a jste si opravdu jisti, ze se jedna o ni?
Podle me ten bocni tlak nema s touto silou nic spolecneho. Podle me je zpusobena rozdilem mezi delkou trajektorie, kterou musi vytah urazit pri zemskem povrchu a na geostacionarni draze. Ta je priblizne 6,61x delsi a proto, aby zustala zachovana stejna uhlova rychlost, se i rychlost vytahu ve smeru trajektorie musi adekvatne zvednout z 464m/s na 3066m/s.
Proto podle me nejde o Coriolisovu silu, ale o setrvacnost toho vytahu. A tak je reseni relativne jednoduche - pravidelne zazehy motoru umistene na vytahu.
A ani ty motory by tam byt nemusely
Ondra Habarcik,2010-01-27 10:30:29
Ale kazdopadne by musely potom byt na te stanici, ale to je otazka toho, co by bylo lepsi a dost by to souviselo s tim, kolik by ten vytah vazil/vlastnosti lana. Pod urcitou vahu by bylo lepsi je mit na stanici, nad urcitou vahu na vytahu.
Korekce setrvačné síly
Stanislav Brabec,2010-01-27 10:41:34
Samozřejmě, že existuje jednodušší řešení než zážehy motorů.
Žádná s projektů orbitálních výtahů nepočítá s koncem lana na geostacionární dráze, ale poměrně vysoko nad ní.
Odstředivá síla by lano napínala a zároveň se s touto boční silou sčítala. Výsledkem by tedy v nejjednodušším případě nebylo namotání lana okolo Země, ale náklon, který by se po zastavení pohybu nákladu směrem vzhůru okamžitě začal korigovat:
Síla směrem nahoru je v dané výšce prakticky konstantní. Při vychýlení lana generuje boční sílu směrem zpět do kolmého směru. Ta roste s náklonem lana (princip tětivy luku).
Setrvačná boční síla naopak postupně klesá s urychlováním tělesa na místní oběžnou rychlost lana.
Pravda, následkem těchto sil bude kmitání lana.
Ti, co to simulovali, tvrdí, že při vhodné kombinaci délky a pružnosti lana, rychlosti a rozmístění nákladů lze kmitání potlačit.
jen pro upresneni
Ondra Habarcik,2010-01-27 11:01:18
to vyrovnani te bocni sily na lano je mysleno v kontextu toho, aby se ta stanice zustala stale na svem miste behem cesty toho vytahu, aby se nehnula. Samozrejme, ze ta protivaha casem dostane tu stanici tam, kde ma byt a motory tudiz pro tohle potreba nejsou a je to "jen" zalezitost zmen vysky te protivahy.
Stabilizace výtahu
Jan Jelínek,2010-01-26 23:32:50
Pánové dole trochu zamíchali dva problémy do sebe. Jedním problémem je stabilizace kolmá a druhým vyrovnání Coriolisových sil. V prvním případě to znamená udržení napnutí lana v optimální rovnováze. Aby se neutrhlo a neuletělo pryč, ani nespadlo na zem.
Co kdyby optimalizaci napětí lana dělala přímo orbitální stanice (jako protizávaží), která by se mohla sama posouvat po laně nahoru a dolů a tím vyrovnávat napětí? Takže když by dole na zemi nakládali výtah, stanice by se pohybovala "nahoru" a zvyšovala tah směrem nahoru svou vyšší orbitou. Jak se výtah rozjede a bude stoupat, stanice by pomalu sjížděla na orbitu nižší.
Na vyrovnání Coriolisovy síly mne nenapadá nic jiného, než aktivní posun orbitální stanice v horizontálním směru (třeba klasickým tryskovým pohonem?). Co si o tom myslíte?
Burdž Dubaj
Martin Smatana,2010-01-25 21:31:48
V Dubaji už začali, ale zatiaľ sa dostali len do výšky 822 metrov :)
Zase mi ve výpočtech chybí boční síly. & To je
Jan Bilek,2010-01-25 17:59:51
Zdravim a diky za komentare. Pravda je ze cim vic se o tom snazim zjistit tim vic mam pocit ze to panove nemaji moc domyslene. To co se zpocatku zdalo jako super napad se pri blizsim pohledu zacina ponekud rozpadat a misto odpovedi na konkretni otazky nalezam spise obecnou mlhu. Jak jsem jiz napsal v clanku, pokusim se na zname problemy odpovedet + Vase otazky predlozim kvalifikovanejsim osobam a odpovedi zahrnu do pristiho clanku. Pokud toho mate vic nevahejte se podelit at to ma priste nejaky prinos.
re: boční síly
Jiri Zahradil,2010-01-25 09:25:37
No stoupat to nahoru samo nebude, to dá rozum - energie je samozřejmě třeba - ale efektivita by u výtahu měla být mnohonásobně vyšší než efektivita současných chemických raket. Koneckonců je očekáváno vylepšení i jiných parametrů - bezpečnost, provoz a údržba sytému například. V tom jsou ty výhody. Aspoň tak to chápu já.
Zase mi ve výpočtech chybí boční síly.
Jiří Pospíšil,2010-01-25 01:29:49
Stoupající náklad musí být urychlován nějakou boční silou, která musí stoupající předmět zrychlovat tak, aby neodáhl lano dozadu a neskončilo to namotáním všeho na zemi. Soustava není inerciální. Stačí si vzpomenout na bruslaře v piruetě, na kapku, co jde od středu gramofonové desky. Na kolejnice. Zkrátka furt zde nevidím vyjádření Coriolisových sil.
Na zvednutí nákladu, bez bočních deformací, kterým žádné lano takové délky nubude schopné odolávat, bude nakonec potřeba tolik energie, jakoby tam žádné lano nebylo.
To je právě
Tomáš Bartoň,2010-01-25 15:10:32
asi důvod proč tu ještě žádné výtahy nejsou. A krom toho by druhý konec musel být neustále něčím aktivně korigován, protože všechny geostacionární dráhy, ať jsou sebepřesnější, podléhají výkyvům a bez korekcí za nějaký čas by to všechno stejně spadlo. Jaká by byla kupř. trvanlivost spojovacího "lana", rezistence vůči povětrnosti (co s tím udělá námraza? co vichřice?), teplotní roztažnost, tlumení, a co dělat s nákladem který se porouchá někde v půlce cesty... zatím mi přijde víc otázek a problémů než odpovědí a řešení. Těším se na další článek kde o tom snad bude napsáno :-)
Nejsou treba
John John,2010-01-25 18:35:42
Ja nevim, pokud se mi ted zase nezborti fyzika, tak se to lano prece diky tomu ze je napnute bude samo udrzovat v stabilni poloze kolme k zemskemu povrchu kde je zavesene. To lano prece nevisi ze stredu zeme ale z jejiho povrchu.
S boční silou problém není
Pavel A1,2010-01-25 18:39:16
Pokud bude ten výtah ukotvený k zemi a napínán tím že těžiště bude až za geostacionární drahou, tak tu boční sílu dodá země. Pokud bude náklad vytahován nebo spouštěn tak pomalu, aby během toho nedošlo k poklesu těžiště pod geostacionární dráhu, tak se změna rychlosti výtahu přenese na Zemi. Energii k dodání boční rychlosti pak dodá rotační energie Země. Samozřejmě, takovéto uspořádání dále zvyšuje požadavky na pevnost lana.
Jj
John John,2010-01-25 18:46:56
Jeste mi v mem prispevku chybelo ze teziste nesmi pri tom posouvani klesnou tak, aby na nej pusobila nizsi odstrediva sila nez gravitacni. Diky za doplneni :) jsem rad ze se mi neborti fyzika.
2 John john
Tomáš Bartoň,2010-01-25 19:31:22
fyzika se bortit nemusí :-) Ale i když umístím jakoukoli protiváhu na geost. dráhu, tak každý stoupající náklad jí bude maličko, ale neodvratně stahovat dolů, až jeden z některých dalších jí stáhne víc než by měl a... Proto si myslím že bude nutno výšku protiváhy stejně korigovat... což není nic co by mělo něco bortit :-)
stahovanie lana
Ján Padyšák,2010-01-25 21:06:02
Nebude to skôr tak, že (zjednodušene pokiaľ ide len o "sťahovanie lana nákladom k zemi"):
- náklad bude pôsobiť na lano silou odpovedajúcou hmotnosti nákladu a rýchlosti jeho stúpania
- odstredivá sila bude pôsobiť na lano silou závislou na dĺžke lana (tj vzdialenosti konca lana od zeme) a hmotnosti lana
- pokiaľ bude odstredivá sila väčšia ako sila, ktorou pôsobí náklad, zostane lano neustále napnuté...
Ne na ale nad
Pavel A1,2010-01-25 21:08:52
Jenže ta protiváha bude umístěna NAD geostacionární drahou, tedy se bude pohybovat vyšší rychlostí, než je oběžná rychlost v dané výšce a proto bude lano trvale napínat. Je to jako roztočený kámen na provázku - když o ten provázek lehce zavadíte, tak se napne zpátky, a ne že vás ten kámen praští do hlavy.
2 Pavel A1
Ján Padyšák,2010-01-26 07:40:50
jj presne tak som to myslel, pekný príklad :). Pokiaľ však za lanko ľahko zavadím (silou menšou ako je odstredivá sila pôsobiaca na kameň), tak by ani k pribížení kameňa nemalo dôjsť alebo sa mýlim? :).
Tak zvaná protiváha
Tomáš Bartoň,2010-01-26 20:37:32
nemůže být NAD geostacionární dráhou; těleso buď je geostacionární, anebo není, je to jen otázka výšky a oběžné rychlosti a hlavně sil, kterými je to těleso schopno aktivně korigovat svou polohu. Dá se však najít určitá rovnováha mezi rychlostí, výškou a přitažlivostí a objekt může zůstat vzhledem k danému bodu na rovníku "nehybně" bez dalších korekcí. Jenomže lano bude neustále přitahovat "konečnou stanici výtahu" k Zemi - jak svou vahou, tak stoupajícími náklady. Na tom nic nezmění jestli budou náklady tahat silně anebo jen zlehka, síla se prostě musí nějak kompenzovat (viz ISS - vzduch za ní "tahá" tu silněji, tu zlehka, ale díky tomu ISS neustále padá dolů a moduly jí čas od času urychlením strkají zase nahoru) (a ne že mě budete kamenovat tvrzením že tak vysoko vzduch nesahá :-) Čili: kdyby se "konečná stanice" zvedla o něco dál od Země (to je to slovo NAD) a ponechala si svou rychlost, počala by se zpožďovat vzhledem k bodu na rovníku a přestala by být geostacionární. Potřebovala by tedy dopředný impuls aby "dohnala" své geostacionární místo. Jenže v ten moment by počala utíkat od Země pryč a lano by nesloužilo k putování nákladu, ale k přidržení stanice v nějaké výšce - ale to by asi byly síly poněkud jiné než šplhání nákladu. Třeba by to mohla vyřešit nějaká trajektorie lana, to netuším. Asi nebude moc snadné udržet "konečnou stanici" tam kde by měla být :-) Snad jsem nenaplácal příliš nesmyslů, kdyžtak mně opravte :-)
Musí být nad
Pavel A1,2010-01-26 21:27:03
To těžiště výtahu (což se nemusí shodovat s polohou koncové stanice) musí být nad geostacionární drahou, právě aby ten výtah stabilizovalo. Vaše srovnání s ISS je mimo mísu - ISS není na geostacionární dráze a není lanem připoutaná k Zemi. A žádný zákon nepřikazuje tělesům v gravitačním poli se pohybovat jen a právě kruhovou oběžnou rychlostí. Když bude výtah ukotvený na zemi, může (a musí) se těžiště nad geostacionární drahou pohybovat rychlostí vyšší, než je kruhová oběžná rychlost v daném místě, o to, aby to lano neulítlo, se postará to ukotvení na Zemi. Nějaká stabilizace toho těžiště bude samozřejmě zapotřebí, ale nebude na to zapotřebí zdaleka tolik energie, jako na urychlení družice na oběžnou rychlost, protože většina energie se odebere rotaci Země.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



