
Holub domácí je domestikovaná forma holuba skalního. Hodně jich ale znovu zdivočelo a těm se ve městech říká „létající potkani“. Rozšiřují to o nich automobilisté, kteří nemají garáž. Pro nás ostatní s výjimkou těch zvěčněných do soch, velkým rizikem, dokonce ani tím zdravotním, nejsou. Byly doby, kdy jsme je měli i rádi a sdíleli s nimi jeskyně. Holubí bystré smysly nás prý včas varovaly před nebezpečím. Časem ale zlenivěli a začali se přiživovat na výplodech našeho zemědělčení. I pak náš vztah k nim zůstal veskrze kladný. Vraceli jme jim to pojídáním holoubat. Možná proto z něj pohané udělali kultovní zvíře symbolizující lásku a plodnost. Takové věci se z hlav těžko vyhánějí a tak se posvátné zvíře pohanů převtělilo do symbolu nebeského míru u křesťanství, židovství i islámu.
Staří Egypťané měli bohů tolik, až v nich měli zmatek a tak místo mírotvorných snah na holubech oceňovali loajálnost a jejich schopností využívali ve zpravodajských složkách a armádě. Římani před zbožností dávali přednost gurmánství a tak z nich udělali něco jako velkochov na maso.

I když holubí pošta byla dlouhou dobu našich dějin prakticky nejrychlejším způsobem jak si dopravovat zprávy, nad tím, co jim propůjčuje jejich navigační schopnosti jsme se moc nepozastavovali. Připisovalo se to jejich dobrému zraku. Pak si někdo se špatným spaním všiml, že ptáci létají i v noci a tak se naše představy rozrostly o orientaci pomocí hvězd. Problém nastal až když jiný mudrlant začal do toho šťourat poznámkou, že létají i když je zamračeno. Korunu tomu pak dala Italka, která publikovala, že se její holubi měli snahu vracet správným směrem i když jim předtím přerušila zrakový nerv, což v praxi znamená totéž, jako by jim vypíchala oči. I když její argument byl také jen statistikou, bylo obtížné ho jen tak smést se stolu. Tak začala snaha vysvětlit věc existencí biologického magnetometru, orgánu nahrazujícího kompas. Přesvědčení bylo tak silné, že ho vědci nakonec našli. Doložili to výsledky histologických a rentgenologických analýz a stali se slavnými. Celé to měly mít pod palcem struktury obsahující železo v povrchové vrstvě horní části zobáku poštovních holubů. Teorie biomagnetometru zabalená do formulací o dendritech trojklaného nervu s místy s výskytem železa a jejich uspořádáním podél vláken axonů, dále pak existenci tří dendritických oblastí na každé straně zobáku se specifickou trojrozměrnou orientací i dvoustrannou symetrii celého systému, se stala věrohodnou.

Ale jen do doby, než to zopakovala jiná parta, které se to zdálo příliš krkolomné. Ze záhadných vezikulů v dendritech schopných reagovat na změny magnetického pole se rázem vyklubaly obyčejné makrofágy a z magnetosenzitivních neuronů byly ze dne na den jen bílé krvinky, které krom mikrobů, spolykaly i rozpadlé a odumřelé buňky, včetně erytrocytů. Právě jejich železo hledače magnetorecepce zmátlo. Ti, kteří si chtěli z omylu německých vědců zvlášť škodolibě vystřelit, dávali k dobru fakt, že dendritické struktury s železitými biominerály v zobáku má i kdejaká slepice. Proč zmiňovali drůbež? Jejím předkem je totiž nemigrující asijský kur bankivský a ten orientaci magnetorecepcí k dlouhým tahům opravdu nikdy nepotřeboval.
Orientaci pomocí magnetického pole Země považovali mnozí hned zpočátku za nesmysl. Například proto, že jedinec by se musel s takovou mapou v hlavě už narodit. Jinak by se v neznámém prostředí totiž nezorientoval. To se nelíbilo hlavně genetikům. Takovou složitost by evoluce totiž musela hodně dlouho vymýšlet, než by našla způsob jak mapu do mozku potomků od rodičů přenášet. Nehledě na vzniklé nesmysly, které by holátkům v hlavách vznikaly, kdyby v sobě při svých migracích našly zalíbení páry z různých koutů světa.
Nejen genetici, i fyzikové většinou kroutí nad výmyslem etologů hlavami. Poukazují při tom na vrtkavost naší matičky Země, která si občas usmyslí a přepóluje se. To by ale vymyšlenost, kterou evoluce vyvíjela miliony let, v mžiku udělalo nejen k nepotřebě, ale i ku škodě. Evoluční biologové také varují před přeceňováním geniality evoluce. Mmožná by zvládla tak složitou věc vymyslet, ale ne prakticky od píky znovu a znovu. I další argumenty, jako třeba činnost našich energetiků a jejich drátování země vedeními o vysokém napětí, této teorii moc nesvědčí. Jenže i ve vědě jsou módní vlny a tak hledání orgánu snímajícího zemský magnetismus má zastánců stále dost. Jen se nikdo z nich moc nezamýšlí nad tím, jak by ptáci mohli vnímat sklon vektoru magnetické polarizace, jeho odchylku od vodorovné polohy. Inklinaci sledující zeměpisnou šířku, deklinaci s lokálním odklonem magnetického severu od geografického a tím určovat zeměpisnou délku. A ani nad tím, jak by se pro magnetickou orientaci našlo v malých mozečcích dost místa pro složitý a sofistikovaný „software“, včetně archivu uložených magnetických map zděděných po předcích. Bez takové mapy by v neznámém terénu byl pro ptáka celý složitý aparát prakticky k ničemu.

Mnohým „mapařům“ se pojetí magnetorecepce začíná jevit příliš narážející na ostří Occamovy břitvy a tak se z toho pokoušejí vybruslit alternativou. Tou by měla být jiná mapa. Ptáci by si ji do svých mozečků začali vtiskovat již od narození. Moc by k tomu nepotřebovali, jen vnímat směr vanoucího větru, jeho specifickou vůni, vlhkost,... což by jim posléze mělo usnadňovat orientaci i tam, kde ještě nebyli.
Podle vědců z Cornell University by se zase holubi měli navigovat podle infrazvuku. Akustické vlny o frekvencích pod 10 Hz jsou v atmosféře běžné. Generují je větry, bouřky, přechod frontálních poruch, magnetické bouře, polární záře, vlny v oceánech, zemětřesení i člověk svými stroji. Naší pozornosti unikají, protože je neslyšíme. O holubech je ale známo, že infrazvuk vnímají a mohli by se tedy jím i řídit, kdyby chtěli. Na ruku této teorii jde šuškanda holubářů. Rázové vlny nadzvukových letadel jim prý kazí závody. Něco by na tom být mohlo. Infrazvuk se šíří i stovky kilometrů a mohl by ptákům vytvářet jakési zvukové mapy. Tak třeba horské štíty postavené větru do cesty mohou být jakýmisi zvukovými bójemi. I tato teorie má své mouchy a odpůrce. Ptačí navigace totiž funguje i v době, kdy se infrazvuk krajinou zrovna nenese.
Jakoby všichni ale tak nějak zapomínali, že na řadu podivností, jakou je registrace směru sever-jih, stačí poloha slunce na obloze, nebo polarizace modré složky slunečního světla. Očaři, jak se přezdívá těm, co dávají přednost vizuální orientaci, dlouho upozorňují na schopnost ptáků vnímat polarizované světlo. To má jednu ohromnou přednost, dá se tím určovat směr i když je zataženo. Dovedou to i primitivnější tvorové, jakými jsou například milovníci výkalů – vrubouni. I na oslovi jsme psali o tom, jak to afričtí borci zvládají i v případě světla odraženého od Měsíce a jak pracovat s polarizovaným světlem jim nedělá problém. Noční tahy ptáků v době nepřízně počasí a kdy je pod mrakem, by se tím vysvětlit daly. Záhadou zůstává, jak to dokážou ti oslepení. Jejich počet při pokusech ale nebyl až tak přesvědčivý, aby se případné přání nemohlo stát otcem myšlenky. Ostatně pomocí slunečního kamene v podobě dvojlomného kalcitu (známého spíš jako islandský vápenec) fungujícího jako polarizační filtr pomocí něhož lze zjistit rovinu polarizace běžného denního světla a tím určit kterým směrem je za oblaky ukryté Slunce, se v neznámých vodách dovedli orientovat i staří Vikingové. Navíc nemuselo jít jen o kalcit. I turmalín a další minerály mohou posloužit stejně dobře. A ptáci to nejspíš zvládají také.
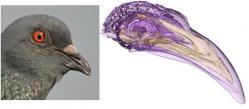
Svou troškou do mlýna k objasnění orientace ptáků se nyní pokusil přispět i švýcarsko – ukrajinský tým. Ptáci prý disponují gravitační mapou a někde v těle mají mít vnitřní gyroskop. Hans-Peter Lipp působící na universitách v Curychu a jihoafrické KwaZulu-Natal se považuje za holubáře. Stal se jím prý už v době, kdy sloužil ve švýcarské armádě. Nenadchly ho ani holubí „mapy zápachů“ ani ty geomagnetické. Přichází proto s vlastní představou k níž se dopracoval spolu s Valerijem Kanevskyim z ukrajinského Technologického institutu. Ten byl nejspíš iniciátorem prověření ptačí paměti na gravitační situace jejich domovské oblasti a využívání takové mapy k navigaci. Oba výzkumníky ta myšlenka posedla natolik, že jí podrobili zkoušce praxí. Jak sami říkají, gravitační mapy by byly holubům k ničemu, pokud by neměli gyroskop. Lipp a Kanevsky nyní na toto téma publikovali článek v časopisu The Journal of Experimental Biology. V podstatě jde o popsání události, jak gravitační anomálie ptáky matou a z toho vyvozený závěr, že ptáci mají svůj vnitřní gyroskop.
K ověření své gyroskopové teorie navigace potřebovali výzkumníci lokalitu, kde by gravitační anomálie nebyly komplikovány těmi geomagnetickými. Ty by totiž do jejich pokusu vnášely rušící element a oponenti by namítali, že jde o záležitost magnetorecepce. Takové místo Kanevsky se svým kolegou Vladimírem Entinem údajně našli. Má jít o velký kruhový kráter vytvořený kdysi dávno dopadem meteoritu. Jsou v něm místa s gravitací slabší než je v daném místě obvyklé. Vycházeli z toho, že pokud jsou jejich úvahy o orientaci holubů podle gravitačních anomálií správné, pak by okraj jejich kráteru musel „gyroskopovou navigaci“ holubům rušit a to by se projevilo na trasách ptáků. K pokusu přizvali holuby chovatele z nedaleké vsi Novoukrajinka. Ptačí dobrovolníky před vlastním pokusem zvykali nosit baťůžek. 26 ptáků, kteří se nakonec vzdali protestů proti taštičce s GPS navigací odvezli do středu kráteru a pak je nechali, ať si poradí, jak umí. Zajímali se jen o jejich baťůžky a to, co zaznamenaly.
Z 18 holubů, kterým se podařilo domů s nákladem úspěšně dorazit, se jich sedm hned na začátku „trefilo“ do směru, kde gravitační anomálie při okraji kráteru prakticky nebyly. Ti překonali okraj kráteru, nevychylovali se nijak zvlášť z kurzu a po překročení okraje kráteru jen zkorigovali svůj směr a zamířili si to rovnou domů. Ptáci, kteří vyrazili jinými směry, se jevili být nad okrajem kráteru s gravitační anomálií dezorientovaní. Když překročili druhou gravitační poruchu, znovu jakoby chaoticky měnili svůj azimut a vydávali se třemi různými směry. Sergei Guskov a David Wolfer tvrdí, že porovnáním drah letu ptáků, a zjištěním, že ty jedince, které „postihly“ gravitační anomálie, měli chaotičtější a méně přímé trasy letů domů, než ti, u nichž počáteční náhoda při startu je zavedla na cestu bez anomálií, neznamená nic jiného, než že ptáci mají gyroskop. Pomocí něj „čtou“ aktuální data a porovnávají je s těmi svými domovskými. Podle toho korigují směr svého letu. To, že někteří z jejich ptáků brouzdali krajinou i několik dní, než se jim podařilo najít cestu do rodného hnízda, by podle nich mělo vysvětlovat ještě jednu věc navíc. A sice, že holubi se jen zřídka uchylují k alternativním navigačním strategiím, které by jim mohly napravovat chyby poňoukané jejich vnitřním gyroskopem.
Zni to natolik tajemně a zajímavě, že se dalo předpokládat, že se to bude líbit. Má to však stejně hořkou příchuť jako má teorie vyznavačů magnetorecepce. Stejně jako jejich teorie, autoři tohoto výzkumu také nemají nejmenší tušení, kterým orgánem by gravitaci holubi mohli detekovat, ani jakými buněčnými receptory a mechanismy by tak slabé síly byli holubi schopni zaznamenat.
Teoreticky by funkci gyroskopu mohlo „hardwarově“ zvládat statokinetické ústrojí a holub odvážený z domova by mohl zaznamenávat směr, rychlost, dobu otáčení (získat tak výsledný úhel) a rychlost a dobu dalšího pohybu,... následně pak z jednotlivých vektorů si průběžně skládat "relativní mapu" z bodu A do B. Pravdou je že taková "mapa" (přesněji neustále aktualizovaný, výsledný vektor)
by se nemusela dědit, nicméně i tato představa naráží na problém. Je jím dostatečně přesné zpracování a vyhodnocení údajů a jejich zapamatování. Hlavní námitkou asi je, že během přesunu zvířat cestou necestou, kodrcání v neznámem a stísněném prostředí, by ptačí mozek sužovaný stresem nesměl ani na chvilku udělat výpadek a nezapočítat třeba jednu jedinou zatáčku. I to by z výpočtu konečného vektoru udělalo paskvil.
Navzdory vážným pochybnostem se už o existenci ptačích gyroskopů píše jako o hotové věci. Jen media většinou opomíjí uvést, že jde o spekulaci a ještě k tomu založenou na statistice chování ani ne dvaceti opeřenců.
Literatura: Blaser, N., Guskov, S. I., Entin, V. A., Wolfer, D. P., Kanevskyi, V. A. and Lipp, H.-P. (2014). Gravity anomalies without geomagnetic disturbances interfere with pigeon homing - a GPS tracking study. J. Exp. Biol. 217, 4057-4067. jeb.biologists.org/content/217/22/4057
Holubi magnetické pole „slyší“?
Autor: Dagmar Gregorová (05.05.2012)
V ptačích zobácích magnetoreceptory nejsou
Autor: Dagmar Gregorová (25.04.2012)
Diskuze:
Každý černobílý pohled je zavádějící
Karel Wágner,2014-11-28 07:48:12
Tradiční představa aristotelovských pěti základních smyslů (zraku, sluchu, hmatu, chuti a čichu) se neustále rozšiřuje, přičemž např. všechny schopnosti člověka uvědomit si předmět nebo jev, který působí na smyslový orgán, nejsou zdaleka ještě probádány. Natož pak u zvířat. Samo vnímání, podmiňující orientaci člověka i zvířat v prostoru a čase, představuje složitý proces, při kterém žádný tvor nikdy nevnímá pouze jediným smyslem, ale vždy všemi svými (i třeba dosud nepopsanými) smysly. Celé vnímání člověka i zvířat lze pak chápat jako komplex navzájem se doplňujících a ovlivňujících smyslových počitků či vjemů, přičemž zde platí, že výsledný celek je kvalitativně něco jiného, než jeho jednotlivé části.
Coriolisova sila sa neda cítiť
Tomáš Habala,2014-11-19 21:16:58
K úvahám o Coriolisovej sile treba povedať, že táto sila sa nedá cítiť. Nejedná sa totiž o zmenu pohybového stavu objektu Coriolisovej sily, ale o zmenu stavu referenčného prostredia. Keďže prostredie je referenčné, zmenu vzťahujeme na objekt. Dobre je to vidno tu:
https://www.youtube.com/watch?v=mcPs_OdQOYU&list=PLE20A7EE21E09FBC7
Za ideálnych podmienok, za úplného bezvetria, by holub dostatočne rýchlo letiaci pozdĺž poludníka zaznamenal, že sprava, alebo z ľava fúka vietor. To sú všetky pocity, ktoré by mohol mať.
V tom se mýlíte
Pavel Brož,2014-11-19 22:26:04
Představte si, že po tom poledníku jede konstantní rychlostí vláček, a na podlaze jeho vagónu leží kulička. Předpokládáme, že vláček nedrncá, pro jednoduchost zanedbejme i tíhové rozdíly dané jednak zploštěním Země a jednak různě velkou odstředivou silou na různých zeměpisných šířkách (pokud by nám to přece jen vadilo, vláček by mohl jet místo po poledníků po rovnoběžkách, tím bychom se problémů jak se zploštěním, tak s proměnnou zeměpisnou šířkou vyhli). Zanedbáme-li tření, kulička se na podlaze začne valit ve směru, v němž na ni působí Coriolisova síla - tj. na severní polokouli doprava, na jižní doleva od směru vláčku (pokud se tedy vláček zrovna nepohybuje v blízkosti rovníku).
Nyní si představte, že holub má takovou kuličku (nějaké minitělísko) uvnitř sebe v nějaké dutince, která je pevně spojená s jeho tělem. A to tělísko tlačí na nějaký citlivý nerv. Přesně jak to navrhnul pan Kaštánek.
Moje rozepře s panem Kaštánkem není o tom, že by toto nebylo principiálně možné, já pouze tvrdím, že velikost příslušného Coriolisova zrychlení je tak malá, že bude mnohonásobně přebita jinými obecně nepredikovatelnými zrychleními - některá přitom pocházejí od mávání křídel, jiná od i velice slabých nárazů větru, jiná od manévrování během letů, a ještě jiná dokonce od takových přirozených fyziologických dějů, jako je např. tlukot holubího srdce.
Pokud byste měl na všechny tyto necoriolisovy vlivy dostatečně precizní teorii, která by je všechny dokázala z nějakých dat predikovat, plus pokud byste měl schopnost nezávisle (tj. jinak než oním tělískem) detekovat všechna data působící ta necoriolisova zrychlení (např. z nějakých nezávislých senzorů měřit absolutní rychlost větru v okolí holuba včetně nárazových změn), tak potom byste byl teoreticky schopen z celkového zrychlení, které by cloumalo tím tělískem, vyeliminovat kýženou Coriolisovu část. Navíc byste musel mít k dispozici dostatečně výkonnou "výpočetní" kapacitu (tj. dostatečně výkonný mozek holuba), aby byl schopen všechny tyto informace zpracovávat v reálném čase. Tak přesně tohleto já na rozdíl od pana Kaštánka považuji za naprostý nesmysl. Podstata jeho modelu ale určitě může k detekci Coriolisova zrychlení sloužit, to panu Kaštánkovi neberu.
na velikosti nezáleží
Stanislav Kaštánek,2014-11-20 01:43:20
Pane Broži, díky \Vám jsem prozřel, horizontální Coriolisova síla záleží na sin(fi), čili na zeměpěpisné šířce. Úhlová rychlost je v rovině pseudovektor a v prostoru vektor ve směru osy rotace. Coriolisova síla je malá. Ano. Sluchové vjemy jsou i velmi slabé ( slyšíme od výkonu zvukových vln 10^-12 W/m2), slyšíme zvuk z různých směru a identifikujeme ho pomocí malinkých rezonátorů ucha. Slyšíme slovo řeka a přestavíme si ji, jsme schopni to slovo říci ve více jazycích, donutit struny hlasivek slovo vyřknout. Prostě příroda se evolucí rozhodla, že je to dobré pro přežití. Podobně jsou z nějakého důvodu přírodě vlastní D-sacharidy, L-aminokyseliny, antiparalení dvojšroubovnice DNA atd. Složitost zrakového vnímání prostoru je nepochybně větší, jak detekce Coriolisovy síly, kterou příroda asi nepotřebuje. Vnímání magnetismu a elektromagnetických polí příroda nepreferuje, je to asi dobře, protože bychom se z toho zbláznili.
Dvojice holoubek a holubička vypuštěná na svatbě asi za 600 Kč pro majitele uletí 100 km za 5 hodin a jsou v pohodě doma a všichni jsou spokojeni.
Jdu si zobnout zrnko magnetovce, abych trefil do postele :)
Pro : Stanislav Kaštánek 20.11.2014 v 01:43
Karel Wágner,2014-11-20 13:11:02
V případě elektromagnetických vln se mýlíte. Ty vyzařují všechna lidmi používaná elektronická zařízení, proto se také již celá desetiletí vedou vášnivé debaty o tom, zda elektromagnetický šum o nízkých intenzitách má nějaký vliv na biologické procesy, včetně procesů v lidském organismu. Přičemž dosud nebyl u člověka žádný vliv antropogenního elektromagnetického pole pod limity stanovenými Světovou zdravotnickou organizací v řádných, dvojitě zaslepených experimentech prokázán. Řada badatelů po celém světě tak pod dojmem dosavadních poznatků dospěla k zevšeobecňujícímu závěru, že antropogenní elektromagnetická pole o nízkých intenzitách nemají na biologické procesy žádný vliv. Avšak díky studii týmu prof. Mouritsena nazvané „Antropogenní elektromagnetický šum narušuje orientaci magnetického kompasu u stěhovavých ptáků“, kterou 15. května 2014 otiskl prestižní vědecký časopis NATURE, již tento závěr neplatí. Neboť týmu prof. Mouritsena se podařilo vůbec poprvé prokázat, že uvažovaný magnetický kompas stěhovavých ptáků úplně selže, když jsou ptáci vystaveni uměle lidmi vytvářenému (antropogennímu) neionizujícímu záření ve formě rádiových vln, i když je jeho intenzita hluboko pod mezními hodnotami, které by podle Světové zdravotnické organizace (WHO) a Mezinárodní komise pro ochranu před neionizujícím zářením (ICNIRP) mohly mít škodlivý vliv na živé organismy. Jinak řečeno, tým prof. Mouritsena zdokumentoval jasný a reprodukovatelný vliv antropogenních elektromagnetických polí, nejčastěji označovaných za elektromagnetický smog, na obratlovce.
Pre pana Broza
Tomáš Habala,2014-11-20 20:39:14
Zdá sa, že som zmiernil polemiku s pánom Kaštánkom. :) Vlak je veľmi dobrý príklad, možno najlepší. Objekt má v každom okamihu voľnosť len v jednej dimenzii a v ostatných dvoch je pevne pripojený k referenčnému prostrediu. Môže sa v tom prostredí pohybovať z bodu A do bodu B a zároveň zaznamená rozdiel pohybového stavu prostredia medzi týmito bodmi.
V každom prípade, aj keď uvažujeme o vlaku, ak tam človek sedí so zaviazanými očami, nevie, či ho to na stenu vlaku tlačí kvôli tomu, že vlak zatáča, nakláňa sa alebo je to tá Coriolisova sila. Na tom nič nezmení ani špeciálny orgán.Tak isto ani holub nevie, či ten bočný vietor je Coriolisova sila alebo obyčajný závan.
pan Habala - ad boční vítr a Coriolisova síla
Pavel Brož,2014-11-20 21:15:00
Je pravda, že celkově působí vždy jen celkové zrychlení dané součtem všech dílčích. Nicméně může do toho ještě zasáhnout adaptace. Tak např. my lidé jsme jako všichni suchozemští živočichové adaptováni na tíhová zrychlení cca 1 g. Nedokážeme sice rozlišit jeho podstatu, např. kdyby nás přemístili na obří kosmickou loď tvaru rotujícího válce, kde bychom stáli uvnitř válce hlavou směrem k jeho ose, tak při vhodné obvodové rychlosti bychom nepoznali se zavázanýma očima rozdíl. Na toto zrychlení jsme adaptováni a nijak ho nevnímáme. Pokud jsme ale vystaveni jinému zrychlení, rozdíl pocítíme celkem rychle, a už při cca 8 g dokonce ztrácíme vědomí. Pokud se vrátíme k tomu rotujícímu válci, tak se zavázanýma očima bychom nic zvláštního necítili, pokud by naše odstředivé zrychlení bylo právě rovno 1 g. Pokud by ale rotace válce mírně kolísala, poznali bychom to velice spolehlivě.
Jinak ty polemiky si tak neberte, s panem Kaštánkem rozhodně má smysl polemizovat, protože má racionální argumenty. To když třeba jiný diskutující vehementně tvrdil, že sluneční aktivita zvyšuje sopečnou aktivitu, tak jsem po chvíli sebepřemáhání jakoukoliv polemiku vzdal jako zbytečnou. S panem Kaštánkem se dá přít konstruktivně, doufám, že i se mnou je to podobné.
Pre pana Broza
Tomáš Habala,2014-11-20 22:13:53
S týmto súhlasím.
Čo sa týka polemiky, mal som na mysli len to, že vaše stanovisko a stanovisko pana Kaštánka sa opticky priblížili, pri porovnaní s pohľadom, ktorý som prezentoval.
má holub vibrační gyroskop jako hmyz?
Stanislav Kaštánek,2014-11-21 00:17:17
Pane Broži, psal jsem 19.11 na konec části diskuze Je to běs..., ale nějak se mi to sekalo, tak jsem to nedokončil a přešel na toto vlákno.
Souhlasím s Vámi, zvláště v tom, že mozek účinně FILTRUJE a efektivně zpracovává data. Hmat- má hloubku, s čímž mají senzory robotů problém. Dlaň ruky cítí padající hrubou mlhu nebo dotek kousku 1 cm vlasu ( řekněme hmotnost 4E-8 kg), ale skoro nevnímáme ocelovou tyč 80 kg činky, tedy na dlaň 40 kg, což je 1 000 000 000 x větší zatížení. Lední medvěd vyčenichá (mrtvého ?) tuleně na 10 km. Motýl v jednom pokusu údajně reagoval máváním křídly na několik málo molekul feromonu (myslím to bylo uváděno jako 10^-17 g). Prostě vyhodnocení mozku nelze srovnávat výchylkou na siloměru v jedoucím vlaku v zatáčce.
http://cs.wikipedia.org/wiki/Coriolisova_s%C3%ADla
Zvířata. Dvoukřídlí (diptera) a motýli (Lepidoptera) využívají Coriolisovu sílu při letu: kyvadélka u dvoukřídlých, respektive tykadla u motýlů rychle kmitají a hmyz je využívá jako vibrační gyroskopy. V tomto případě Coriolisův efekt nesouvisí s rotací Země.
Existuje též teorie, která zdůvodňuje sklon delfínů ke kroužení na levou, respektive pravou stranu, když spí. Proti této teorii je též řada námitek. Přesto může jít o pohyb po tzv. inerciálních kružnicích. Pozn.moje: tyto inerciální kružnice jsou nejvíc zatočené ( jsou nejmenší) v blízkosti pólu. Je tam i obrázek pro rychlost 60 m/s. Tento obrázek
http://upload.wikimedia.org/wikipedia/commons/thumb/6/69/Coriolis_effect14.png/220px-Coriolis_effect14.png
ukazuje, že Coriolisova síla je stejná podél rovnoběžek, ale roste s rostoucí zeměpisnou šířkou. Což plyne i ze vzorce pro horizontální Coriol.síly.
Takže holub by se musel ve směru rovnoběžek rozhodnout podle Slunce. Nepotřebuje navigaci na každém metru, ale stačí globální směr.
Stránka o balistice :
http://www.fsps.muni.cz/inovace-SEBS-ASEBS/elearning/strelba/balistika
"Coriolisova síla vzniká rotací Země a působí na každý objekt na Zemi, který se pohybuje nerovnoběžně s osou rotace Země. Způsobuje stranovou a výškovou odchylku střely. Na severní polokouli je stranová odchylka vždy doprava, na jižní doleva. Výšková odchylka závisí na směru výstřelu."
http://forum.gunshop.cz/vn-jsi-balistika-novy-program-t3298.html
diskutér King : ve smyslu, že střela m=168 g, v=800 m/s, vzdálenost = 1000 m, 50. stupňů severní šířky. Coriolisova odchylka horizontální VE VŠECH SMĚRECH ( na sever, východ, jih, západ) bude 9,9 cm.
Můj názor: Rychlost rovnoběžná s osou rotace a budu na 60. šířce. Když si globus postavím tak, že osa rotace je svislá, tedy jsem ji odklonil o 23,5° , bude taky vektor rychlosti svislý, čili při přímočarém pohybu touto rychlostí bude těleso stále stejně daleko od osy rotace. Rovník je rovnoběžný s rovinou stolu a spojnice z 60. šířky do středu Země je pod uhlem 60° k rovině stolu a současně kolmo k povrchu Země. Střela vypálená rovnoběžně s povrchem na sever by měla svírat s rovinou (stolu) rovníku úhel 30°. Při pohybu na sever podle povrchu se
vzdálenost k ose zkracuje a nastává přebytek kinetické ( v podstatě rotační) energie tělesa nad povrchem, který nese těleso ve směru rotace, tedy na východ ( v trajektorii doprava). Žádný rovnoměrný pohyb v "rovině" povrchu tedy nemůže být rovnoběžný s rotační osou, jedině tečna na rovníku ( nejzřetelněji ve směru poledníku), Coriolisova síla bude na rovníku nulová. Směr po povrchu v blízkosti severního pólu bude takřka kolmo zkracovat vzdálenost k ose rotace, Coriolisova síla bude největší ( sin (fí) se blíží 1.
http://cs.edaboard.com/topic-4390217.0.html
"Fyzikální princip vibračního gyroskopu: vibrační objekt má tendenci udržet vibrující části ve stejné rovině, čímž se otáčí. Je tedy mnohem jednodušší a levnější, než je konvenční rotační gyroskop na podobnou přesností.
Ve strojírenské literatuře, typ zařízení, je to také známý jako Coriolisův vibrační gyroskop, protože jako rovina kmitání je otočena a odpověď zjistí snímače výsledky z Coriolisova výrazu v jeho pohybové rovnice.
Implementace. Piezoelektrický gyroskop: Piezoelektrické krystaly lze přimět vibrovat a boční pohyb v důsledku Coriolisova síla je možné
měřit, tím produkovat signál týkající se rychlost rotace."
Rozumím tomu o něco líp, jak na začátku diskuze, jestli tomu může rozumět ten holub, to nevím.
http://cs.wikipedia.org/wiki/Holub_st%C4%9Bhovav%C3%BD
"Holub stěhovavý (Ectopistes migratorius) býval pravděpodobně nejhojnějším ptákem na Zemi. Obýval v obrovských hejnech původní listnaté lesy Severní Ameriky, východně od Skalnatých hor. Jejich počty dosahovaly až dvou trilionů jedinců a odhaduje se, že tvořili 40 % všech severoamerických ptáků. Po osídlení Ameriky bílými přistěhovalci byli loveni kvůli masu i pro zábavu, takže jejich počty rychle poklesly. Poslední divoce žijící holub stěhovavý byl zastřelen v roce 1900, poslední jedinec uhynul v roce 1914."
Holubí navigace selhala, správný směr byl pryč z Ameriky.
ptákoviny ve Wikipedii
Stanislav Kaštánek,2014-11-21 00:40:00
http://cs.wikipedia.org/wiki/Holub_st%C4%9Bhovav%C3%BD
o kus dál dole v téže stránce je rozumné číslo počtu holubů stěhovavých, tedy ne 2 triliony:
"Odhaduje se, že v době objevení holuba stěhovavého tvořili holubi až 40 % všech ptáků Severní Ameriky a odhaduje se také, že celková populace čítala 3-5 miliard jedinců."
Ad filtrování vjemů a Coriolisova síla
Pavel Brož,2014-11-22 01:31:54
Takhle, s tím filtrováním vjemů si hlavně neustále musíme připomínat jednak relativní velikost té síly, a jednak která data ten letící holub může reálně sbírat. Nejprve k té relativní velikosti síly. Je dobré mít na paměti, že horizontální Coriolisovo zrychlení, které při rychlosti holuba cca 20 ms^-1 je na zeměpisné šířce Prahy rovno 0,0022 ms^-2, tedy cca dvě desetitisíciny g, působí ve výsledku naprosto stejně, jako kdyby se holub vůči tíhovému poli Země vychýlil zrovna o dvě desetitisíciny radiánu, což je 41 úhlových vteřin. Můžeme si to taky představit, jako by holub seděl na pět metrů vysokém bidle, a měl by rozpoznat, jestli to bidlo stojí absolutně kolmo, anebo jestli ho někdo předtím, než se na něj holub usadil, vychýlil o pouhý jeden milimetr na těch pět metrů délky. Aby toho byl holub schopen, musel by disponovat neuvěřitelně přesným nezávislým smyslem (nebo soustavou smyslů) detekujícím směr tíhového zrychlení, který by byl citlivý s přesností nejméně na desetitisíciny g, a který by přitom byl „hluchý“ vůči vlivu Coriolisova zrychlení. Potom byste teoreticky mohl porovnáním smyslových údajů z orgánů vnímajících celkové zrychlení (včetně Coriolisova) se smyslovými údaji vnímajícími (s přesností na desetitisíciny) pouze tíhové pole bez Coriolisova zrychlení, vyfiltrovat to čisté Coriolisivo zrychlení. Přičemž by nám tam stále zůstaly viset nezodpovězené otázky, jak odfiltrovat vlivy např. pohybů vzdušných mas, nebo tlukotu srdce (srdce ptáků během letu pracuje velice vydatně), nebo zrychlení zakoušená během změn směru letu holuba, přičemž tyto vlivy až o dva až tři řády převyšují velikost Coriolisova zrychlení.
Co se týče té Coriolisovy síly na rovníku, ono je to ve skutečnosti ještě složitější. Horizontální složka Coriolisovy síly je na rovníku nulová jak ve směru poledníků, tak ve směru rovníku, prostě horizontální složka tam vymizí v obou směrech. Celková Coriolisova síla ale na rovníku vymizí jenom ve směru poledníků – ve směru rovníku bude nenulová, a její směr bude kolmý k „hladině moře“ (málem bych napsal k „zeměploše“, prostě mám na mysli směr od středu Země k rovníku :-)) Tato vertikální složka samozřejmě nepřispívá k horizontální složce Coriolisovy síly, o kterou se většinou zajímáme. Nyní by bylo záhodno vysvětlit, proč se o tu vertikální složku většinou nezajímáme. Roli zde hrají tzv. vazby – pokud se zajímáme např. o vliv Coriolisovy síly na toky velkých řek, tak tam tou vazbou je dno řeky, a vazbovou silou je tam tíhové pole, které té řece neumožní vytékat z povrchu Země do vesmíru, ale táhne tu vodu dolů, kde jí ale v dalším pohybu (do středu Země) brání to dno řeky. Díky této vazbě nám efektivně zbývají dva volné směry pohybu, oba dva jsou horizontálními směry, a to je přesně ten důvod, proč tu vertikální složku Coriolisovy síly u rozboru těchto systémů ignorujeme.
Podobně když se zabýváme pohybem vzdušných mas, např. vznikem hurikánů, tak tam také uvažujeme jistou vazbu. Atmosféra je sice systémem třírozměrným, nicméně opět díky tíhovému poli můžeme při rozboru vlivu Coriolisovy síla na rozsáhlé oceánské bouře tu vertikální složku zanedbat, a to proto, že ta vazbová síla – tj. tíhové pole – nám opět zajistí, že nám ten hurikán neodletí někde do vesmíru, ale zůstane pěkně přilepený v několika málo nejnižších kilometrech atmosféry, a zůstane tam přilepený i během několika celých otoček Země kolem její osy (protože hurikány nezřídka trvají i několik dní). Kdyby tam ta vazba nebyla – tj. kdyby tam nebyla ta vazbová síla (tíhové pole) a povrch Země, tak by se hurikány vyvíjely samozřejmě úplně jinak, než jak vídáme na družicových snímcích.
Bohužel typické výklady podstaty Coriolisovy síly, včetně ukázek s tím rotujícím diskem na wikipedii, jsou příliš zjednodušené a ignorují právě vliv těch vazeb u typických systémů, u kterých se o vliv Coriolisovy síly zajímáme. Typicky studované systémy totiž nemají podobu rovnoměrně přímočaře se pohybujícího tělesa, ale mají podobu dějů, jejichž pohyb je těmi vazbami limitován na blízkost zemského povrchu či na úzkou vrstvu atmosféry.
Zvuková vlna
Stanislav Kaštánek,2014-11-22 03:14:24
Pane Boži, já netvrdím, že hlub se naviguje Coriolisovou silou. Je to síla malá a složitá a příroda to asi nevyvíjela solo pro holuba. Pro Coriolisovo zrychlení horizontální na 50.rovnoběžce a=0,022 m/s2, hmotnost čidla 0,1 gram, tedy m=0,0001 kg, doba působení t=0,1 s, vyjde dráha s= 0,00011 m, síla F=0,0000022 N, práce po této dráze W=2,42E-10 J. Řádově 1E-10 J.
Zvuk má mez slyšitelnosti intenzita zvuku P= 1E-12 W/m2. Za t= 0,1 s vykoná zvuková vlna práci 1E-13 J/m2 , to je 1E-18 J/cm2. A ještě mozek identifikuje výšky zvuků a jejich směry, nejen intenzity. A syčení hada vyhodnotí jako nebezpečí. Tlukot blízkého srdce vyhodnotí jako bezpečí.
Rozuzlení bude každopádně zajímavé
Pavel Brož,2014-11-22 19:38:48
Říše živých organismů si umí někdy svá tajemství udržet i desítky let, navzdory všetečnému zkoumání celé řady i velice chytrých lidí. Po dlouhá léta byl např. záhadou let čmeláka, i slovutní odborníci na aerodynamiku si na tomto problému vylámali zuby, protože podle jejich výpočtů byla vztlaková síla generovaná křídly čmeláka sotva poloviční k tomu, aby ho mohla udržet ve vzduchu. Dnes už víme, že jedna část z chybějící poloviny jde na vrub viskozity vzduchu, kterou na škálách srovnatelných s velikostí hmyzu už nelze zanedbat tak, jak to můžeme činit na škálách větších. A zbývající část z té druhé poloviny je působena obrvením čmeláčích křídel plus jejich speciálním pohybem, velice odlišným od toho, jak křídly mávají ptáci – čmeláčí křídlo opisuje při svém pohybu zhruba velké L, a v té vertikální fázi díky svým brvám vytváří mikroskopické turbulence, které ve výsledku přispívají ke vztlakové síle.
Nedivil bych se, kdyby ještě dlouholetější záhada ptačí navigace byla nakonec vyřešena podobně, jako kombinace dvou či více faktorů, které byly dlouhou dobu přehlíženy, přičemž ale žádný z nich nepředstavuje nějakou extra revoluci v chápání biofyziky toho děje.
Poděkování
Igor Sedlák,2014-11-18 14:14:42
Jeden z nejlepších článků poslední doby, včetně diskuse. Zajímavé a navíc jsem už dlouho tak dobře nepobavil u oběda, ještě teď vybírám drobky z klávesnice!
Gyroskopem je sám pták.
Roman Nováček,2014-11-18 10:21:34
Na kroužícího ptáka působí corriolisova síla snadno měřitelné velikosti a jeho vestibulární aparát by měl dát dohromady zeměpisnou šířku, takže je možné, že žádný speciální aparát ptáci nepotřebují. Jediné co je třeba nějak vykompenzovat je síla větru a to si dokážu představit, že u zvířete pro které je vzduch místo denodenního pobytu dokáže vzdušné proudy odhadnout. Ostatně corriolisovu sílu si můžete užít na kolotoči při zakývání hlavou. U člověka vyvolá kinetózu, u ptáka pomůže nalézt souřadnice :-)
pro Nováček
Stanislav Kaštánek,2014-11-18 13:46:51
Pták m=1kg, v=10 m/s, čelní průřez S = 50 cm2= 0,0050 m2, součinitel odporu vzduchu C= 0,1, hustota vzduchu =1,3 kg/m3.
Bude mít tíhovou sílu G= 10 N,
odporová síla vzduchu F = 0,0325 N.
Coriolisova síla nejvýše F = 0,00145 N . Čili tato Coriolisova síla je pro celého ptáka moc malá k ostaním vlivům.
Nějaký vodorovně uchycený jazýčekovitý lísteček s možností citlivě uvnitř dutinky se vyklánět vpravo/vlevo k čidlu s citlivými chloupky za rovnoměrného letu kupředu by měl vykompenzovanou gravitaci jako krakorcový nosník o odpor vzduchu uvnitř dutiny není. Jak už jsem psal Coriolisova síla pro 10 mg bude nejvýše F = 1,45E-8 N.
Také včely mají schopnost se orientovat do určité vzdálenosti a vrátit se zpoět a dokonce si to "tanečky" na česle předávají. Létají ve dne, hlavně podle Slunce a "počítá" čas letu potřebný k návratu. Daleko chytřejší holub by potřeboval si uložit směr a dobu působení (Coriolisovy) síly jazýčku na své čidlo. Převozem holuba nějakou rychlostí a převládajícím směrem tento záznam vznikout může.
Kinetosa na kolotoči je podle mě způsobena prudkým pohybem okolí, člověk by se měl dívat na sedátko před sebou, které je realtivně v klidu. Coriolisova síla činí zlomky promile odstředivé síly.
Klasické vysvětlení magnetické orientace ptáků má dobré důkazy.
http://www.lidovky.cz/radiove-vlny-rusi-ptaky-0we-/veda.aspx?c=A140519_155830_ln_veda_ape
"„U ptáků máme hodně nepřímých důkazů, že jde o chemický kompas. Magnetické pole ovlivňuje chemické reakce, při kterých vznikají páry volných radikálů,“ vysvětluje Pavel Němec. Chemický kompas pravděpodobně zprostředkovávají bílkoviny zvané kryptochromy, které mají ptáci v oku. U rypošů a dalších savců se zatím jako pravděpodobnější jeví mechanismus související s biologicky syntetizovaným magnetitem – mikroskopickými částicemi, které jsou citlivé vůči magnetickému poli."
Pane Nováček, pták není gyroskopem
Pavel Brož,2014-11-18 21:39:17
pak by totiž musel být gyroskopem každý pohybující se předmět, jako např. auto, lokomotiva, letadlo. Nenechte se mýlit, gyroskop je název vyhrazený pro úplně jiná zařízení, viz např. zde: http://en.wikipedia.org/wiki/Gyroscope . Najdete tam spoustu variací gyroskopů, ale žádný není založený na objektech, jako jsou např. letící ptáci. Mezi variacemi gyroskopu tam najdete např. i tzv. Coriolisův vibrační gyroskop, na ten odkazoval i pan Kaštánek v jeho odkazu: https://otik.uk.zcu.cz/bitstream/handle/11025/2996/BP_Jiri_Steno.pdf?sequence=1 na str. 19 a 20. Ovšem nenechte se mýlit – Coriolisův vibrační gyroskop měří jinou Coriolisovu sílu, než je ta vzniklá v důsledku otáčející se referenční soustavy pevně spojené se Zemí, o které se tu celou dobu bavíme. Coriolisův vibrační gyroskop měří Coriolisovu sílu danou otáčením samotného gyroskopu, a veličinou, která je tímto zařízením měřena, je právě ta rychlost otáčení toho gyroskopu (jinými slovy, je to zařízení, které, když je uzavřete nějakého rotujícího boxu, tak dokážete přesně změřit, jak rychle se ten box otáčí, a to měření uvnitř tohoto boxu).
Dále – vestibulární aparát žádného živočicha neumí dát dohromady zeměpisnou šířku – jak by prosím Vás mohl? Vestibulární aparát reaguje především na změny polohy živočicha, a u některých živočichů navíc na jeho polohu vůči tíhovému poli (tento aparát se dá např. u lidí snadno zmást, jak prokazují četné pokusy s neudržením rovnováhy v místnostech, kde je interiér postaven záměrně našikmo, nicméně třeba zrovna ptáci jsou schopni registrovat svou polohu vůči tíhovému poli bez problémů). Žádný vestibulární aparát ale není schopen poznat, na jakém stupni zeměpisné šířky se živočich nachází.
Jinak Coriolisovu sílu spojenou s otáčením Země si můžete užít při jízdě v jakémkoliv dopravním prostředku, nejlépe v letadlech. Zažíváte v jejím důsledku kinetózu? Přitom v letadlech jste vystaveni až jedenáctkrát většímu Coriolisovu zrychlení, než ti holubi, plus navíc nejste vystaveni náhodným zrychlením, která ti holubi musí během letu zakoušet. Čím to asi tak bude, že tu Coriolisovu sílu necítíte? Myslíte, že je to tím, že vestibulární systém holuba je o několik řádů citlivější, než ten lidský? Nenechte se mýlit, pak by se do toho holuba pro svou velikost vůbec nevešel.
Gyroskopy už mají i telefony
Andrea Marlova,2014-11-18 05:32:04
iPhone 4 má kromě akcelerometru i gyroskop. K čemu? http://iphonemania.mobilmania.cz/iPhone+4+ma+krome+akcelerometru+i+gyroskop.+K+cemu
Tomáš Habala,2014-11-17 21:36:01
naozaj pekny popis, precital by som si aj viac...a aka je vami preferovana teoria orientacie stahovavych vtakov?
Tento rok pripevnili jednemu orlovi v Tatrach gps pristroj a on pravidelne smskoval svoju polohu, dalo sa to sledovat on-line na internete. Bolo fascinujuce vidiet, ako orol hned na Slovensku nabral kurz na Bospor, aby nemusel letiet nad morom, preletel po vychodnom pobrezi Stredozemneho mora a pozdlz Nilu letel az pod rovnik.
moc rád bych věděl, jak to dělají
Pavel Brož,2014-11-17 22:54:30
Tyto experimenty orientací ptáků mě fascinují, naprosto ale netuším, jak to zvládají. Mimochodem, ptáci vidí i v UV oboru, zatímco my máme v oku tři druhy čípků, ptáci mají čtyři. Dalo by se vlastně říci, že jejich barevný prostor má o jednu dimenzi více, než náš. Léta se toho např. využívalo v kontrole kvality elektronických součástek - holubi byli naučení ty špatné vyhazovat z pásu, dokázali rozpoznat i ty, které byly lidským okem nerozeznatelné (zřejmě ale když ve výrobním procesu došlo k nějaké abnormálnosti, odrazilo se to třeba ve spektru tak, že to ten holub byl schopen poznat). Myslím ale, že i tuto práci nakonec i za holuby převzala nějaká automatizace.
Je to běs ... je to běs!
Pavel Brož,2014-11-17 19:41:35
Je to opravdu tragédie, co se občas vylíhne i v renomovaných odborných časopisech. Osobně si myslím, že tento a podobné články jsou velice potřebné z didaktického hlediska, protože ukazují, že i věda je plná nejen omylů, ale občas i pěkných nesmyslů, z nichž některé se dokážou propasírovat i do impaktovaných vědeckých periodik.
Nicméně k věci:
Klasický gyroskop je nástroj, který je asi nejméně vhodný k detekci gravitačních anomálií. Účelem gyroskopu je totiž primárně udržovat rotační osu tělesa v daném směru, a to bez ohledu na okolní vlivy. Ideální sféricky symetrický gyroskop směřuje svou osu úplně stejným směrem dokonce i při úplných obězích kolem Země. Pro tuto svou vlastnost se gyroskopy s úspěchem používají např. ve vesmírných sondách a různých vesmírných laboratořích, jako jsou např. vesmírné teleskopy. Osa ideálního sféricky symetrického gyroskopu se podle Newtonovy teorie nehne dokonce ani tehdy, když sonda prolétá v blízkosti Jupitera za účelem svého urychlení. Teprve pokud vezmeme na pomoc Einsteinovu obecnou teorii relativity, dostaneme malilinkaté stáčení osy ideálního gyroskopu. Tento jev byl dokonce změřen družicí Gravity Probe B, a jeho hodnota činila 6,6 tisícin úhlové vteřiny za rok (teda za cca 5400 oběhů družice kolem Země).
Pokud ovšem uvažujeme nikoliv ideální gyroskop, pak se jeho osa působením vnějšího gravitačního pole může stáčet. Jedná se např. o precesi zemské osy, která je způsobena primárně gravitační silou Měsíce v důsledku zploštění Země a náklonu její osy. Jinými slovy, protože Země není dokonalá koule, ale je díky své rotaci mírně zploštělá, a protože Měsíc neleží v rovině rovníku, tak se svou gravitací snaží zemskou osu „narovnávat“ – ve skutečnosti je výsledkem působících sil nikoliv narovnání zemské osy, ale její precese s periodou cca 23 tisíc let. Pokud bychom tedy místo ideálního gyroskopu vzali např. rotující disk v Kardanově závěsu (ve skutečnosti právě tato konstrukce je nejčastější, protože v rámci přesnosti bohatě postačuje pro drtivou většinu praktických aplikací), tak pak bychom mohli v silně nehomogenním gravitačním poli uvažovat o tom, že bychom mohli pomocí nepatrné precese osy měřit tuto nehomogenitu (nebo chcete-li, gravitační anomálii).
Nyní si dáme soutěžní otázku: Henry Cavendish, který jako první měřil gravitační sílu mezi tělesy v laboratoři (určitě si pamatujete na onu dobovou ilustraci s olověnými koulemi), použil torzní váhy místo gyroskopu protože:
a) to byl úplný blbec
b) nebyl dost šikovný na to, aby sestrojil gyroskop
c) torzní váhy jsou na nehomogenity gravitačního pole nesrovnatelně více citlivější než gyroskop
Možná už tušíte, že správná odpověď je c. Dokonce ani neideální gyroskop totiž není ani trochu vhodný pro určování gravitačních nehomogenit, tedy ani pro určování gravitačních anomálií. Pokud by v nějaké pohádce dostal Honza na výběr mezi určováním gravitační anomálie s pomocí gyroskopu a přenášením vody sítem, určitě by si měl vybrat to druhé.
V praxi se ale gravitační anomálie (přesněji tíhové anomálie) měří nikoliv torzními vahami, ale pomocí měření doby kyvu kyvadel, nebo pomocí měření doby volného pádu, anebo pomocí gravimetrů, které fungují podobně, jako těleso zavěšené na pružině, kdy velikost gravitační síly je úměrná velikosti výchylky z rovnovážné polohy. Nejlepší gravimetry dosahují přesnosti až 10^-8 ms^-2 (tedy miliardtiny normálního tíhového zrychlení g).
Z gravimetrické mapy České Republiky na: https://www.ig.cas.cz/userdata/files/popular/Gravimetricka_mapa.pdf
vidíme, že typické tíhové anomálie jsou na našem území řádu stovek mikrometrů s^-2, tj. řádu několika stotisícin g. Proto uvažovat o tom, že by se holubi mohli řídit změnou směru gravitačního pole je naprostý nesmysl – pokud se totiž např. na vzdálenosti 10 km změní velikost tíhového zrychlení o jednu stotisícinu, směr tíhového zrychlení se změní o cca 2 úhlové vteřiny. Nyní si k tomu vezměme, že holub letí, mává křídly, a nikdy kolem něj není dokonalé bezvětří. Pokud bychom dokázali naše nejlepší gravimetry zmenšit na tak malou velikost, aby jej holub unesl, tak bychom na letícím holubovy oné preciznosti 10^-8 ms^-2 nedosáhly ani náhodou, protože tyto přístroje potřebují precizní kalibrace a vyloučení vibrací, nedají se provozovat např. na trampolínách, a už vůbec ne na holubech, ať už stojících nebo letících.
Co se týče zmínky o supercitlivém vestibulárním aparátu v jednom z příspěvků níže, je to opět o něčem jiném. Vestibulární aparát hlídá relativně rychlé změny polohy (např. když holub na hřadě klimbá a mohl by ztratit rovnováhu a spadnout, vestibulární aparát mu dá včas vědět díky tomu, že tekutina v něm protékající v důsledku změny polohy pohne příslušnými řasinkami, jejichž pohyb vygeneruje odpovídající nervový vzruch. Změna o stotisícinu g na vzdálenosti cca 10 km neudělá s těmito řasinkami ani tolik, co mrknutí holubího očního víčka.
Taktéž jakékoliv zmínky o využití Coriolisovy síly jsou úplně mimo. O Coriolisově síle mimochodem koluje velice urputný mýtus, podle nějž má určovat, jakým způsobem rotuje voda v umyvadlech na severní a jižní polokouli. Je to naprostá pitomost, běžné konstrukční asymetrie ať už ve tvaru umyvadla, nebo ve tvaru přepážek v odtoku, stejně tak jako pouhé naklonění umyvadla o zlomky milimetru, působí řádově větší síly, než je Coriolisova, a to nemluvím o zbytkových vírech po napouštění umyvadla, které přetrvávají i několik hodin. Samozřejmě pokud bychom měli holuba o velikosti srovnatelné s velikostí typického hurikánu, Coriolisovu sílu bychom si ani náhodou nemohli dovolit ignorovat. Jinak je to ale nesmysl.
Občas si tak říkám, že se kolikrát nezaslouženě cítíme povznesení nad to, čemu lidé věřili např. v devatenáctém století – tehdejší teze, jako že maximální rychlost dopravního prostředku nesmí převýšit 40 km/hod, protože jinak by cestující zemřeli zalknutím, anebo že nelze sestrojit létající stroj těžší vzduchu, na to všechno dnes můžeme reagovat blahosklonným úsměvem. My už jsme samozřejmě mnohem chytřejší. Po desítky let cpeme školou povinná dítka špenátem s odůvodněním, jak hodně je v něm železa. Publikujeme články, ve kterých se krávy při pastvě natáčejí podle směru magnetického pole. A představujeme si, že holubi mají v hlavách gyroskopy. Ještě že ti holubi neumí mluvit.
díky
Matyáš Patlevič,2014-11-17 21:20:56
moc pěkný popis technické stránky gyroskopu a meření tíhového zrychlení! Teď už i psi močí podle magnetického pole. A dokonce za tento objem můžeme děkovat českému vědci z ČZU. Jméno jsem bohužel zapomněl, ale dostal letos IG nobelovu cenu. Čas snad ukáže, jak se holubi orientují...
:-)
Pavel Hudecek,2014-11-17 22:01:41
Ta představa měření gravitačních anomálií na třepajícím se holubovi mi přišla natolik ujetá, že jsem si ani nevšimnul nesprávného použití pojmu gyroskop... mj. asi i proto, že se dnes celkem často zaměňuje s tříosým akcelerometrem.
Výklad o Coriolisově síle mi zas připomněl jistou africkou atrakci: Na břehu moře, těsně u rovníku, si lze zaplatit ukázku toho slavného víru: Týpek naloží turisty do loďky, odplave kamsi na moře, pak do lavoru nabere vodu, vytáhne špunt a ukáže vír. Pak odplave kousek jinam (údajně na druhou stranu od rovníku) a pokus znovu předvede, tentokrát s opačným vírem. Má to ale jeden háček: Pokud u večeře víc lidí pustí videa z těchto "experimentů", zjistí, že sice všichni dodržují to, aby směr v jedné a druhé části výletu byl opačný, ale neshodují se na tom, zda má být na severu vpravo a na jihu vlevo, nebo naopak. Obě kombinace údajně často předvede i tentýž týpek, jen s jinými skupinami na palubě:-)
Tak a teď přemýšlím, že bych zašel do sklenářství a zverimexu, nakoupil myši, dal do čtvercového akvárka, to omotal dvěma kolmými cívkami a zkusil, zda bude závislost preferovaných směrů na magnetickém poli. Pokud ano, tak co se stane, bude-li pole rotovat:-)
Jisté je pouze to, že největší radost bude mít moje kočka a had bývalého podnájemníka:-)
co se týče té Coriolisovy síly
Pavel Brož,2014-11-17 22:45:19
tak tam mnoho lidí tápe i v tom, že si neuvědomuje, že Hurikány se netočí ve stejném směru, v jakém působí Coriolisova síla, ale přesně v opačném, důvody jsou vysvětleny v odstavci "Proudění v okolí tlakové níže" zde: http://cs.wikipedia.org/wiki/Coriolisova_s%C3%ADla . Jinými slovy, zatímco má Coriolisova síla údajně stáčet toky velkých řek na severní polokouli po směru hodinových ručiček, tak hurikány se otáčí proti směru hodinových ručiček.
Mimochodem ale, jako didaktický příklad je ten argument s velkými řekami krajně nevhodný. Takové řeky, na kterých by to bylo demonstrativně vidět, se totiž na mapě světa dost špatně hledají. Coriolisova síla samozřejmě existuje, plyne elementárně při prostém matematickém přepisu Newtonových zákonů do rotující soustavy, v tom chyba není. Chyba je v tom, když si umaneme, že to automaticky musí stáčet velké toky daným směrem, a ignorujeme specifičnost lokální geografie, která kolikrát hraje podstatně větší roli, než uniformně působící Coriolisova síla. Prostě vytrhneme jednu vybranou vlastnost modelu světa, a všechny ostatní vlastnosti chceme považovat za podružné. V důsledku toho pak po celé generace přežívají vyloženě nepravdivá tvrzení, jako je např. onen mýtus o vírech v umyvadlech, které se mají točit podle Coriolisovy síly.
Díky
Ondi Vo,2014-11-17 23:05:46
nenapsal bych to zdaleka tak výstižně. :-)
Ovšem humorné teorie jsou přece také zábavné a bez vtipu by byl život nudnější.
Panu Hudečkovi :
To představení s lavórem jsem viděl v jednom TV-cestopisu. Někde na rovníku, asi v Equadoru, počítám, je místo s milníkem dělící Zemi na severní a jižní polokouli a na zemi je vydlážděno pár metrů rovníku.
Ten domorodý bavič měl lavór se zašpuntovanou dírou na oprýskané železné trojnožce a za úplatu spustil "vědecký" výklad coriolisovy síly. Takto poučenému publiku předved nalití vody do lavóru stojícím severně od "rovníku" a dokázal odšpuntováním a následným směrem rotace víru existenci oné síly. Načež přemístil onen lavór o metr jižněj, tedy na jižní polokouli a demonstraci opakoval. Vír se mu poslušně vytvořil v opačném směru. Šikulka.
Coriolisova síla
Stanislav Kaštánek,2014-11-18 00:17:31
Pro Brož.Velikost Coriolisovy síly je malá pro malé rychlosti, ale stačí k zatáčení velkých sibiřských na sever tekoucích řek doprava, což je vidět na každé mapě.
F_c= 2*m*omega x v *sin (alfa) ( vektorový součin omega*v řeší směr síly, což por výpočet velikosti není podstatné, alfa je úhel vektoru rychlosti s rovnoměžkami)
Úhlová rychlost rotace Země omega = 6,28/T = 6,28/86400 =7,27E-5 ( rad/s)
v = 10 m/s. Rychlost holuba je 10 m/s = 36 km/h.
Hmotnost sledované částice je m= 0,000 010 kg ( = 10 mg).
Maximální možná Coriolisova síla F =2* 0,000 01* (7,27E-5)*10 = 1,45E-8 [N], což je malá síla, ale identifikovatelná u tělíska např. uvnitř nějaké dutiny typu bubínek ucha.
Bez problémů cítíme dotyk vlasů na ruce. Vzal jsem psí chlup a zašimral se s ním po obličeji a kolem oka, je to cítit velmi zřetelně.
Lidský vlas má asi 80 mikrometrů průměr ( 42-95 mikrometrů). Vlas délky 1 cm se ohýbá vlastní tíhou při opření na stole. Čili síla, kterou se kouskem vlasu dotýkáme obličeje je dobře smysly vnímána.
Hmotnost 10 mm lidského vlasu je asi 5E-8 kg, čemuž odpovídá tíhová síla asi 5E-7 [N]. Těleso z bílkoviny průměru asi 0,5 mm má zhruba stejnou hmotnost kolem 5E-8 kg.
Než odpovíte, pošťourejte se chloupky na předloktí v oku n nebo na rtech.
Re: Coriolisova síla
Pavel Hudecek,2014-11-18 00:27:51
Pane Kaštánku, teď zkuste s tím vlasem určit směr CS za jízdy na kole po dlažbě, abyste získal přibližnou představu, jak by to asi dělal holub za letu.
pro Hudecek
Stanislav Kaštánek,2014-11-18 08:23:49
Máte pravdu, Coriolisovu sílu neucitím, ale přilepil jsem si izolepou zrnko magnetovce pod oko a při jízdě na kole magnetická navigace funguje dobře.Takže je to jasné :)
Pane Kaštánku, Vy jste skutečný expert :-)
Pavel Brož,2014-11-18 21:04:35
Takže podle Vás to alfa ve výrazu F_c= 2*m*omega x v *sin (alfa) je úhel vektoru rychlosti s rovnoběžkami :-))) No, fyziku jste evidentně nestudoval, což je dobře, jinak byste byl pro Vašeho zkoušejícího velice smutnou vizitkou. Sdělím Vám jedno tajemství – to alfa není žádný úhel vektoru rychlosti s rovnoběžkami, to alfa je obyčejná zeměpisná šířka. Žádnému fyzikovi to ale neříkejte, protože fyzici to samozřejmě ví.
Takže nyní, když se podařilo demystifikovat záhadu úhlu alfa, tak už se nemusíme omezovat na řeky tekoucí směrem na sever nebo na jih, protože Coriolisova síla nezávisí na tom, kterým směrem řeka teče. Koukněme se na takový Dunaj nebo Mississippi. Mimochodem, poměr Coriolisova zrychlení na 29. stupni severní šířky (což je např. New Orleans) ku Coriolisovu zrychlení na 69. stupni severní šířky (což je např. Murmansk) je cca 52 procent, takže se nejedná např. o řádový rozdíl, pro Dunaj je ten rozdíl ještě menší. Takže kde že to vidíme zatáčet Dunaj a Mississippi doprava? Ono to nijak očividně průkazné není, nemám pravdu? Ono to totiž není očividně průkazné ani u těch sibiřských řek, protože je jasné, že nebudou téct do Černého moře, ani se neprokoušou Čínou do Indického oceánu, ony prostě musí nevyhnutelně skončit v tom Severním ledovém oceánu. To je celá záhada toho jejich stáčení. Tím samozřejmě neříkám, že Coriolisova síla na tyto řeky nepůsobí, tím jenom říkám, že rozhodujícím faktorem pro jejich tok je lokální geografie, daná především reliéfem kontinentu, který byl utvářen všemožným vrásněním v průběhu jeho historie. Toto především určuje tvar toku řeky, nikoliv Coriolisova síla, která je zde podružná.
No a nyní se podívejme na potenciální schopnost holubů registrovat Coriolisovu sílu. Coriolisovo zrychlení např. na zeměpisné šířce, jakou má Praha (cca 50 stupňů sev. šířky) činí pro rychlost letu holuba cca 20 m/s (údaj jsem vzal z anglické wikipedie viz: http://en.wikipedia.org/wiki/Columbidae#Flight ) zhruba 0,0022 ms^-2. Při nárazu větru o velikosti delta_v=1 m/s za jednu sekundu by byl holub vystaven bočnímu zrychlení cca pětsetkrát většímu, než je ono Coriolisovo zrychlení. Dokonce i když tento náraz umenšíme na delta_v=10 cm/s během jedné sekundy, což už s obtížemi zaregistrujeme, přičemž takovýchto mininárazů vzniká i během velice krásného slunečného počasí obrovské množství, tak stále dostáváme padesátinásobek Coriolisova zrychlení. Přitom holubi během letu občas zatáčejí (typické trajektorie letu holuba viz např. zde: http://www.plosone.org/article/fetchObject.action?uri=info:doi/10.1371/journal.pone.0077102.g005&representation=PNG_M ), plus navíc jsou vystaveni dalšímu nemalému zrychlení v důsledku mávání křídel – rozbor letu ptáků např. zde: http://homepage.univie.ac.at/Heinz.Kabelka/SVP/Flug/pe7_4_004.pdf ). To všechno vede k tomu, že holub je během svého letu neustále vystavován působení nepravidelných zrychlení o několik řádů převyšujících Coriolisovo zrychlení.
A teď mi prosím Vás vysvětlete, jak nějaké tělísko uvnitř dutinky v holubově těle tato zrychlení rozliší? Chcete snad říct, že holub je vybaven dalšími senzory, které dokážou velice precizně odfiltrovat nárazy větru, síly zrychlení působící při změnách směru letu či flapové síly vznikající máváním křídel, a dokáže všechny tyto vlivy s požadovanou přesností integrovat během celého letu, aby poznal co z toho činí Coriolisovo zrychlení? Takový holub, pane Kaštánku, by byl hotovou létající laboratoří :-)))
Coriolisova síla a úhel vektorů
Stanislav Kaštánek,2014-11-19 00:15:48
Pane Broži,
http://cs.wikipedia.org/wiki/Coriolisova_s%C3%ADla
Pročtěte si sekci Výpočet, řádka asi pátá se vzorcem
F_c = -2m*omega*v*sin (theta)
kde úhel theta je úhel sevřený mezi vektorem úhlové rychlosti a vektorem rychlosti. Úhel theta tedy není zeměpisná šířka, jak mě plísníte, ale právě ten úhel s rovnoběžkou (ta má stejný směr jako vektor úhlové rychlosti) . Se zeměpisnou šířkou to pochopitelně souvisí, protože při pohybu po rovníku je stejný směr obou vektorů a tedy Coriolisova síla = 0.
Ano, Coriolisova síla působí na celé severní polokouli při pohybu doprava, psal jsem to hned v prvním vstupu, co řešíte s Dunajem mezi horami, to nevíte asi ani sám. Dobře, řeka jen Ob tekoucí v lautr rovině se jednoznačně zatáčí doprava. Wiki :“ Zjevné je to při pohledu na tvar sibiřských řek“.
Ani znalci biologie si s navigací těch holubů neví rady. Na jak ubohých impulzech je založen zrak, který má dobrý kdejaký hmyz? Co to je za pidiimpulzy, které rozkmitají volný jeden konec desetitisíců drobných různě dlouhých rezonátorů uchycených jedním koncem v uchu? Rozeznáme zvuky, i když nám vítr fouká do uší.Kdyby příroda pracoval evolucí podle vašeho přístupu-NIC NEJDE A NEMŮŽE FUNGOVAT, tak není ještě ani u žížaly. Je dle Vaší logiky u malé Coriolisovy síly kvůli tomu ucho a oko větší jak člověk? Myslíte, že záchvěvy větru a boční zrychlení nepůsobí na síly magnetického charakteru, pokud se pták řídí jimi? Já, když vytáhnu kompas z kapsy, tak počkám ustálení sil. Při celodenním letu tažný pták využívá i Slunce ( hvězdy), které běží kolem po obloze, dráha letu je relativně přímá, ale vodní ptáci vyhledávají hladiny atd. Prostě jde o víc smyslů . Srovnání s computerem v hlavě není dobré, myšlení (nebo mozkové reakce zvířat) je jev paralelního zpracování dat. Pták nepotřebuje každou sekundu podle magnetismu vědět, kam má letět rovně dopředu.
Coriolosova síla a větší obvodová rychlost
Stanislav Kaštánek,2014-11-19 09:10:17
Pane Broži
http://fyzweb.cuni.cz/dilna/krouzky/sr_rot/k28.htm
F_c =2m*omega*v*sin(alfa)
"kde alfa je úhel mezi vektorem úhlové rychlosti otáčející se soustavy a vektorem rychlosti tělesa. Směr vektoru Coriolisovy síly je kolmý na vektory v a w a tvoří s nimi pravotočivý systém (orientaci lze určit pomocí pravidla pravé ruky)."
Nevím jestli byl znovu obstál u zkoušky z fyziky, ale můj základní dojem Corilisovy síly byl jednoduchý. Těleso hmotnosti m pohybující se mimo povrch ( ve vzduchu) na severní polokouli na sever si přináší větší obvodovou rychlost danou v= omega*R, kde R je vzdálenost od osy rotace. Soustava je rotující , tedy neinerciální, zákon setrvačnosti neplatí. Těleso si sebou přináší větší kinetickou energii, než odpovídá vyšší zeměpisné šířce, kam se dostalo. Rozdíl této energie se projeví jako práce spojená s vychýlením trajektorie tělesa, zhruba jako síla*dráha, čili m*a* dráha, kde zrychlení a souvisí s Corilisovým zrychlením. Žádný zákon zachování rychlosti neplatí, ale smysl je ten, že z nižších šířek si těleso přineslo větší složku obvodové rychlosti ve směru podél rovnoběžky, než odpovídá místu s vyšší zeměpisnou šířkou místa, nad nějž se dostalo. Země se otáčí ze západu na východ, takže v tomto případě ( sibiřských řek tekoucích na sever) bude mít těleso ochylku na východ.
Bavíme se o horizontální složce, ne o vertikální
Pavel Brož,2014-11-19 09:51:37
Pane Kaštánku, bavíme se tady nikoliv o holubech startujících do vesmíru, ani o vlivu Coriolisovy síly na vodopády, bavíme se o vlivu Coriolisovy síly na horizontální pohyby, což je třeba ten tok řek nebo let holubů. Tangenciální složka Coriolisovy síly je rovna 2m*omega*v*sin (alfa), kde úhel alfa (na použitém symbolu samozřejmě nezáleží) je zeměpisná šířka.
Dokonce i pokud vezmeme vzorec zahrnující tu vertikální složku Coriolisovy síly ve tvaru -2m*omega x v, kde x je vektorový součin, tak stejně jste vedle s interpretací toho úhlu - úhel alfa není úhlem mezi vektorem rychlosti a rovnoběžkami, jak opakovaně píšete, ale je to úhel mezi vektorem rychlosti a osou rotace (která je shodná s vektorem úhlové rychlosti).
Takže pokud bereme horizontální složku Coriolisovy síly (pro pozemské děje jako je třeba stáčení hurikánů anebo i potenciálně pro let holubů právě ta horizontální, nikoliv vertikální složka hraje roli), tak dostaneme pro velikost té síly 2m*omega*v*sin(alfa), kde alfa je zeměpisná šířka (ověřte si to třeba na těch stránkách http://cs.wikipedia.org/wiki/Coriolisova_s%C3%ADla , je to řádek nad odstavcem Příčiny. A dokonce i pokud bereme Coriolisovu sílu včetně její vertikální složky (kterou tady ale neřešíme), tak úhel vzešlý z vektorového součinu není úhlem mezi vektorem rychlosti a rovnoběžkami, ale je to úhel mezi vektorem rychlosti a osou rotace. Protože vektor úhlové rychlosti - což pro Vás bude asi překvapení - nemá směr rovnoběžek, jak předpokládáte, ale má směr osy rotace.
gyroskop
Milan Baran,2014-11-17 08:16:55
Sú aj gyroskopy bez pohyblivých častí, je to nejaká cievka vodiča svetla. Možno sú aj iné princípy.
Coriolisova síla
Stanislav Kaštánek,2014-11-17 11:25:49
https://otik.uk.zcu.cz/bitstream/handle/11025/2996/BP_Jiri_Steno.pdf?sequence=1
str.19 a str.20 je gyroskop na základě Coriolisovy síly. Jenomže pořebuje (v obrázku č.8 je vidlice) rotující a vibrující část, dále senzory, prostě rotace a elektronika.
Coriolisova síla by mohla být využita, při pohybu se vše na severní polokouli stáčí doprava, velikost Coriolisovy síly záleží na rychlosti a na úhlu k rovnoběžkám, což je vlastně směr. Prostě nějaká kulička, která tlačí na čidlo na levou nebo na pravou stranu, pták letí zobákem kupředu, takže stačí vpravo/vlevo. Ale bouřňáci létají z Arktidy do Anarktidy a zpět a na jižní polokouli Coriolisova síla stáčí doleva.
Nikdo se nepodivuje, že živočichové mají audiovestibulární systém převelice citlivě reagující na směr gravitace, což umožňuje stát na nohou. Asi v sobotu ukazovali Zázraky přírody, člověk neudrží rovnováhu proti svisle pruhované stěně, kterou někdo šoupe. Čili je zapojeno víc smyslů včetně zraku.
gyroskop
Stanislav Kaštánek,2014-11-17 02:16:16
Gyroskop udržuje směr osy rotace a musí se hodně točit. Co roztáčí gyroskop, překonává tření, jak se odvádí vzniklé teplo v "ložisku". Mají úhoři nebo velryby taky gyroskop? Keporkaci plavou každý půlrok z Havaje na Aljašku přes půl Pacifiku a pak zpět.
Proč ne magnetismus?
Adam Lipovský,2014-11-16 22:55:51
Pokud jsem články o hledání ptačí navigace četl správně, teorie magnetismu nebyla vyloučena - jen se vyvrátilo, že jej cítí zobákem nebo "vidí". Navíc pokusy ukazují, že ptáci mag. pole vnímají (viz např. orientace ptáků v kleci podle mag. pole).
A na co by pták potřeboval mapu? Když jsme v cizí krajině a víme, že cílové město je nějakým směrem, také si vystačíme bez mapy.
P.s.: ani bych se nedivil, kdyby jistou citlivost k mag. poli měla všechna zvířata (jen v různé míře).
Fajne gyroskopy
Karel Wágner,2014-11-16 22:00:05
Tož na Ukrajině je všecko možne, tam maji ty ptači gyroskopy i Ostravaci, co jim řikame kratky zobaci. A včil něco k těm slavnym ukrajinskym kraterum:
Impaktní struktury mají obecně kruhový, případně polygonální tvar v závislosti na tektonice dané oblasti. Velikost a tvar kráteru závisí především na kinetické energii impaktujícího tělesa. Ta se při dopadu přeměňuje především na teplo, na mechanickou energii nárazu a roztříštění a energii seismických vln. Při dopadu se během několika sekund zvýší teplota na několik tisíc stupňů Celsia a tlak dosáhne řádu GPa. Meteorit se rychle vypaří a to způsobí výbuch, jež je vlastní příčinou vzniku kráteru. Proto lze také k identifikaci impaktních struktur s úspěchem využívat všech hlavních metod geofyzikálního průzkumu. Je pravda, že velká porozita (a tudíž nízká hustota autochtonních brekcií) způsobuje negativní tíhovou anomálii. V místě centrálního vrcholku je častá pozitivní tíhová anomálie. Zároveň zde však magnetomertie odhaluje i magnetické anomálie, které jsou poněkud komplikovanější než tíhové, přičemž dominantní zde bývá negativní anomálie. Ta může být u velkých komplexních struktur komplikovaná ještě krátkovlnnými anomáliemi v centru struktury. Obecně zde platí, že příčiny změn magnetického pole jsou komplikované a podílí se zde na nich celá řada mechanismů. Navíc zde elektrické metody odhalují anomálie vodivostní. Impaktní struktury se projevují vyšší elektrickou vodivostí v polohách brekcií a natavených hornin. Je to způsobeno vyšší porozitou hornin a tedy větším obsahem fluid. Přičemž vodivostní anomálie mívá značný rozsah.
Inu, kráter po meteoritu, co může holubům nabídnout jen gravitační anomálii a žádné měřitelné změny magnetických a elektrických polí je dobrá věc. Ale příště z té Ukrajiny místo ptačích gyroskopů raději něco o Karkulce...
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



