Předminulý týden oznámila skupina mladých výzkumníků na Technické Univerzitě v holandském Delftu (TU Delft) pod vedením (také mladého) profesora Ronalda Hansona výsledky svého experimentu, kterým opět potvrdila neplatnost Bellových nerovností, a tím i neplatnost jakýchkoliv klasických alternativ ke kvantové teorii. Jejich výsledek je zajímavý tím, že eliminoval zbývající skuliny v předchozích podobných experimentech, a tím zhatil poslední naděje těch, kteří doufali, že kvantovou teorii bude možné nahradit nějakou jinou a přitom klasickou teorií. Ačkoliv je výsledek Hansonova týmu založen spíše na evoluční než revoluční obměně předchozích experimentů, přesto se stává důležitým milníkem, který definitivně ukončuje debatu o principech, na kterých kvantová teorie může či nemůže stát.
Pokusme se ale nejprve přiblížit podstatu letitého sporu, který byl delftskými výzkumníky definitivně uzavřen.
Už více než sto let poutá kvantová teorie svými kontraintuitivními předpověďmi zájem celé řady fyziků, počínaje Albertem Einsteinem a Nielsem Bohrem, kteří spolu strávili dlouhé disputace nad tím, zda její výsledky jsou fyzikálně akceptovatelné či nikoliv. Albert Einstein byl dlouhodobě nespokojený s podobou kvantové teorie, a pokoušel se ukázat, že tato teorie odporuje základním principům, které podle něj měla ctít každá akceptovatelná fyzikální teorie. Ve snaze dokázat logickou nekonzistenci kvantové teorie zkonstruoval Einstein spolu se svými spolupracovníky Borisem Podolským a Nathanem Rosenem myšlenkový experiment, který, pokud by platila pravidla kvantové teorie, dával podle něj zcela nesmyslný výsledek. Tento myšlenkový experiment vešel ve známost jako tzv. Einstein-Podolského-Rosenův paradox (či kratčeji EPR paradox).
V EPR paradoxu máme elektron-pozitronový pár, který byl vytvořen nejlépe kreací ze srážky protiběžných gama fotonů o stejné energii a opačných hybnostech (jedná se pouze o myšlenkový experiment, ačkoliv dnes umíme elektron pozitronové páry rutinně připravovat, děláme to mnohem efektivněji ve srážkách gama fotonů s atomovými jádry). Protože podle předpokladů byla úhrnná hybnost obou gama fotonů nulová, je tím pádem nulová i úhrnná hybnost vzniklého elektronu a pozitronu, které se tedy od místa svého vzniku vzdalují stejnými, ale opačně orientovanými rychlostmi. Kromě zákona zachování energie a hybnosti musí ale také platit zákon zachování momentu hybnosti, a protože do momentu hybnosti přispívá i vnitřní moment hybnosti částic, tzv. spin, musí mít elektron a pozitron vzájemně opačně orientované spiny.
Spin je typická kvantová vlastnost, která nemá v klasické fyzice žádnou dostatečně přiléhavou analogii. Po jeho objevu ve slavném Sternově-Gerlachově experimentu v roce 1922 se následně zjistilo, že spin mají všechny částice včetně elektronů a fotonů. Později se vyjasnilo, že konkrétně u fotonů spin souvisí s polarizací světla – přesněji řečeno, o spinu se bavíme jako o vlastnosti jednotlivých částic, zatímco u letících svazků částic o stejném spinu hovoříme o polarizaci svazku. Anebo ekvivalentně, u světla můžeme spin chápat jakožto mikroskopickou vlastnost fotonů, kterou makroskopicky pozorujeme jako polarizované světlo (nepolarizované světlo je pak tvořeno fotony majícími nestejné spiny). Tato terminologie se následně přenesla opačným směrem z optiky do fyziky elementárních částic, a proto, když čteme o srážkách polarizovaných svazků těch či oněch částic v urychlovačích anebo o polarizovaných terčích při jejich bombardování částicemi, máme tím na mysli, že spiny částic v příslušných svazcích či spiny jader atomů v terčích mají díky předešlé přípravě stejnou orientaci.
|
Plaketa na Frankfurtském Institutu připomínající experiment Otto Sterna a Waltera Gerlacha (Stern vlevo). Kredit: Wikimedia Commons. Další osudy obou protagonistů se ubíraly po naprosto odlišných cestách. Po převzetí moci nacisty v roce 1933 odešel Otto Stern do USA, kde působil nejprve jako profesor na Carnegieho Technologickém Institutu, a později jako emeritní profesor na Kalifornské Univerzitě. Walter Gerlach se naopak aktivně angažoval v nacistickém Německu a stal se dokonce jednou z nejvýše postavených osob zodpovědných za vývoj nacistické atomové bomby. Na konci války byl Brity a Američany spolu s dalšími německými atomovými vědci zajat a osm měsíců internován, aby jej nezískali Sověti. V roce 1957 pak spolupodepsal tzv. Göttingenský manifest proti vyzbrojení Německé Spolkové Republiky atomovými zbraněmi. |
Podstatu výše zmíněného EPR experimentu je nemožné pochopit bez znalosti dvou klíčových vlastností spinu. Jednou je tzv. nekompatibilita měření průmětů spinu do různých os, a tou druhou je kvantování hodnot jeho průmětu. U obou vlastností se zastavíme, protože obě se prolínají celým zbytkem tohoto textu.
Nejprve se zmiňme o nekompatibilitě průmětů spinu do různých os. V souladu se Sternovým a Gerlachovým experimentem je spin podobně jako polarizace světla směrová vlastnost, kterou bychom tedy měly popsat nějakým vektorem (čili orientovanou úsečkou), který by odrážel směr spinu a jeho velikost. Každý vektor můžeme popsat jeho složkami, což jsou vlastně jeho průměty do námi zvolených souřadnicových os. Vektory jsou nedílnou součástí popisu jak Newtonovské fyziky, tak speciální i obecné teorie relativity, popisujeme pomocí nich rychlosti a zrychlení částic, jejich hybnosti, síly na ně působící, ale také intenzity různých polí, jako je elektrické či magnetické, a mnoho jiných fyzikálních veličin.
Zatímco ale v klasické fyzice není problém změřit všechny tři složky libovolné vektorové fyzikální veličiny, v případě spinu to nelze. Ukazuje se totiž, že pro jednotlivé složky spinu platí Heisenbergův princip neurčitosti, analogicky, jako tento princip platí pro polohu a hybnost částice. Připomeňme krátce, že Heisenbergův princip pro polohu a hybnost říká, že čím přesněji určíme polohu částice, tím neurčitější se stává výsledek následného měření její hybnosti, a naopak. Podobný vztah se dá získat (a experiment jej plně potvrzuje) i pro složky spinu, kdy jakmile určíme přesně složku v jednom směru, ovlivní to rozptyl výsledků při následném měření zbylých složek.
Druhou klíčovou vlastností spinu je kvantování velikostí jeho složek. Tato vlastnost je pro změnu zase podobná s kvantováním energetických hladin v atomu, kdy se elektron může v atomu vyskytovat jen s určitými diskrétními hodnotami energie. Diskrétní energetické hladiny tvoří jakýsi čárový kód povolených energií, který je unikátní pro každý prvek či chemickou sloučeninu, na kterémžto faktu je založena spektroskopie umožňující identifikaci látek analýzou jimi vyzářeného či pohlceného světla. V případě složek spinu je ale povolené množství jeho hodnot mnohem chudší, konkrétně pro elektrony jenom +1/2 a -1/2. Totéž platí pro protony, neutrony, a dále obecně pro všechny elementární fermiony, jako jsou třeba kvarky a neutrina. Naopak složky spinu pro elementární bozony, jako jsou fotony, gluony nebo tzv. intermediální výměnné bozony zodpovědné za slabou interakci částic, nabývají hodnot +1 nebo -1 (v případě intermediálních bozonů mohou nabývat ještě hodnoty 0, kterážto hodnota je pro nehmotné bozony nepřípustná).
Právě zmíněné dvě vlastnosti spinu, totiž nekompatibilita jeho složek plus kvantování jejich hodnot, dává vznik docela zvláštnímu chování při jeho měření, jak nyní popíšeme:
- provedeme-li měření průmětu spinu elektronu ve směru nějaké osy, dostaneme tedy vždy výsledek +1/2 nebo -1/2
- pokud následně provedeme druhé měření téže složky, dostaneme vždy už tutéž hodnotu. Jinými slovy, zatímco u prvního měření jsme pro některé z elektronů dostali výsledek +1/2, a pro ostatní výsledek -1/2, tak u druhého a dalšího měření už dostáváme pro každý z měřených elektronů už tentýž výsledek, jako v měření předešlém
- pokud ale provedeme měření jiné složky spinu, než v předcházejícím měření, tak opět dostáváme zcela náhodně pro některé z elektronů výsledek +1/2 a pro ostatní -1/2.
Pro lepší představu je chování spinu při opakovaných měřeních ilustrováno na následujícím obrázku.
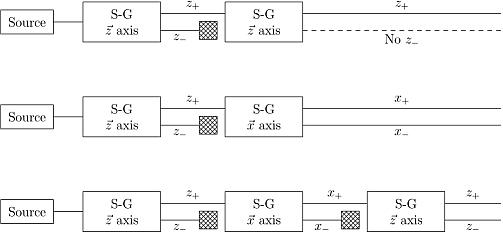
Ilustrace chování spinu při opakovaných měření ve Sternově-Gerlachově experimentu:
Nahoře je opakované měření ve směru osy z, získají se hodnoty průmětu spinu +1/2 a -1/2, označené na obrázku jako z+ a z-. Vybere se hodnota z+, ta pokračuje do dalšího měření ve směru téže osy. Výsledkem je opět táž hodnota, tzn. opakované měření beze změny osy dává identické výsledky jako měření první.
Uprostřed je měření ve směru osy z, následované měřením ve směru osy x. V prvním měření se opět vyfiltruje pouze hodnota z+, která se pošle do druhého Sternova-Gerlachova přístroje. Průmět spinu ve směru osy x je veličinou nekompatibilní s jeho průmětem do osy z, proto je neurčitost druhého měření ve shodě s Heisenbergovým principem neurčitosti rozmazána, a proto se dostanou se stejnou pravděpodobností opět obě hodnoty +1/2 a -1/2, označené jako x+ a x-.
Dole je měření ve směru osy z, následované měřením ve směru osy x, a poté opět ve směru osy z. Po druhém měření se ponechá jenom složka x+, která se pošle do třetího Sternova-Gerlachova přístroje. Výsledkem jsou opět dvě hodnoty z+ a z-. Kredit: Wikimedia Commons
Výše uvedené dvě vlastnosti spinu jsou tou zásadní ingrediencí v EPR experimentu, bez nich by totiž žádný paradox vůbec vzniknout nemohl. Máme elektron a pozitron pohybující se od sebe, přičemž víme, že součet jejich spinů musí být nulový kvůli zákonu zachování momentu hybnosti. Změříme např. u elektronu spin ve směru nějaké zvolené osy, dejme tomu ve směru osy z. Pro tuto z-ovou složku spinu dostaneme jeden ze dvou možných výsledků, dejme tomu +1/2. Díky nulovosti úhrnného momentu hybnosti tím pádem víme, že pozitron musí mít této složky opačnou, tedy -1/2. Elektron tímto měřením zároveň přešel do stavu s hodnotou průmětu spinu +1/2, o čemž se můžeme přesvědčit opakovaným měřením provedeným na tomto elektronu. Vzdálený pozorovatel provádějící na pozitronu stejná měření nám podobně může potvrdit, že on zase dostává opakovaně při měření průmětu spinu pozitronu do směru osy z hodnotu -1/2. Tuto situaci můžeme statistickou terminologií okomentovat tak, že pokud pozorovatel A i B provádí měření stejné složky (tj. průmět spinu do stejné osy), tak jsou jejich výsledky stoprocentně antikorelované.
Pokud by ale pozorovatel B měřil jinou složku než pozorovatel A, dejme tomu y-ovou, tak pak by v polovině případů, kdy A naměřil +1/2, dostal +1/2, a v druhé polovině případů -1/2. Úplně stejně by to dopadlo pro případy, ve kterých by pozorovatel A naměřil -1/2; opět by v polovině těchto případů dostal pozorovatel B výsledek +1/2, ve zbytku pak -1/2. Tuto situaci bychom opět mohli statistickou terminologií okomentovat tak, že v tomto případě mají výsledky obou pozorovatelů nulovou korelaci, tedy že jsou naprosto nezávislé jeden na druhém. Pro lepší představu si opět právě popsané chování ilustrujme na následujícím obrázku.
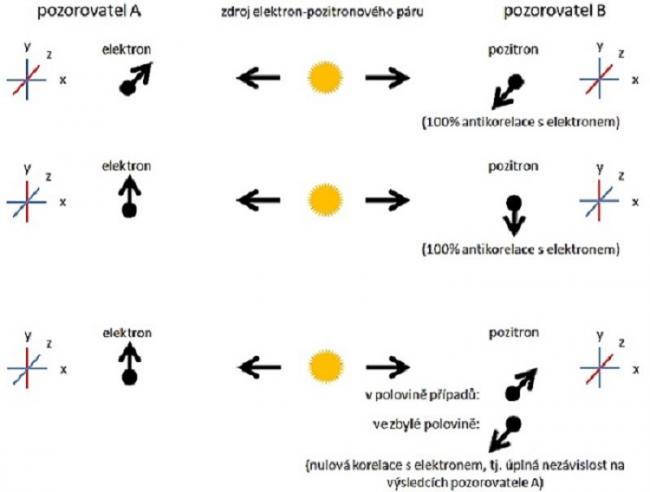
Ilustrace zdánlivého okamžitého přenosu informace v EPR paradoxu:
- v prvých dvou případech měří oba pozorovatelé stejnou složku spinu (nahoře z-ovou, níže y-ovou), a jejich výsledky jsou stoprocentně antikorelované
- ve třetím případě měří každý z pozorovatelů jinou složku spinu (pozorovatel A y-ovou, pozorovatel B z-ovou), a jejich výsledky jsou na sobě nezávislé, tj. mají nulovou korelaci
(kredit: autor)
A o tom je celý EPR paradox, zbývá totiž už jen dodat, že podle kvantové teorie budou oba pozorovatelé dostávat právě popsané výsledky i tehdy, když je budou provádět současně nebo v tak malém časovém odstupu, že signál letící světelnou rychlostí by nestihl přenést informaci s výsledkem jednoho pozorovatele k tomu druhému. A to zní krajně podezřele, speciálně pak pro Alberta Einsteina jakožto otce speciální teorie relativity, která přenosy informací nadsvětelnou rychlostí striktně zakazuje. Hlubším rozborem se dá sice ukázat, že okamžitá změna stavu vzdáleného pozitronu žádnou informaci přenést nemůže, nicméně samotná možnost, že stav vzdálené částice se změní okamžitě, je věcí odůvodněně podezřelou. Einstein takovou nelokální změnu nazval strašidelným působením na dálku, a odmítl přistoupit na myšlenku, že by akceptovatelná fyzikální teorie mohla něco takového obsahovat.
Bylo by dobré si na druhou stranu osvětlit, proč přitom nemůže dojít k přenosu informace od elektronu k pozitronu, a to ačkoliv se stav vzdáleného pozitronu mění už v okamžiku změření spinu elektronu. Klíčem je náhodnost výsledků jednotlivých měření. U nově vygenerovaného elektron-pozitronového páru je totiž výsledek měřením kterékoliv spinové složky zcela náhodný. Zkusme si přesto představit, že se pozorovatel B bude snažit zjistit, které složky spinu se pozorovatel A rozhodl měřit. Udělají dlouhou řadu měření, kterou rozdělí dejme tomu do sad vždy 40 po sobě jdoucích měření, a dohodnou se na tom, že v rámci těchto sad budou měřit vždy stejnou složku, jinak se ale budou rozhodovat zcela autonomně, jakou složku budou měřit. Tzn. že osu měření mohou změnit např. přesně po 40-tém., nebo 80-tém, 120-tém atd. měření, ale ne mezi těmito mezemi. Oba dva pozorovatelé si na začátku sesynchronizují své hodiny, rozejdou se na svá od sebe vzdálená pracoviště, a každé měření provedou v přesně stejný okamžik. Zaznamenají výsledky svých měření, a po skončení odešle pozorovatel A druhému pozorovateli své výsledky, ale bez informace, kterou složku spinu v té které sadě měřil. Pozorovatel B ale porovnáním výsledků i tak spolehlivě pozná, ve kterých sadách měřil pozorovatel A ve stejné ose jako on, protože taková sada bude dokonale antikorelovaná k jeho vlastní sadě (pravděpodobnost náhodné shody je pouze jednu ku biliónu, přesně 1 ku 2^40). Situaci opět ilustruje následující obrázek.
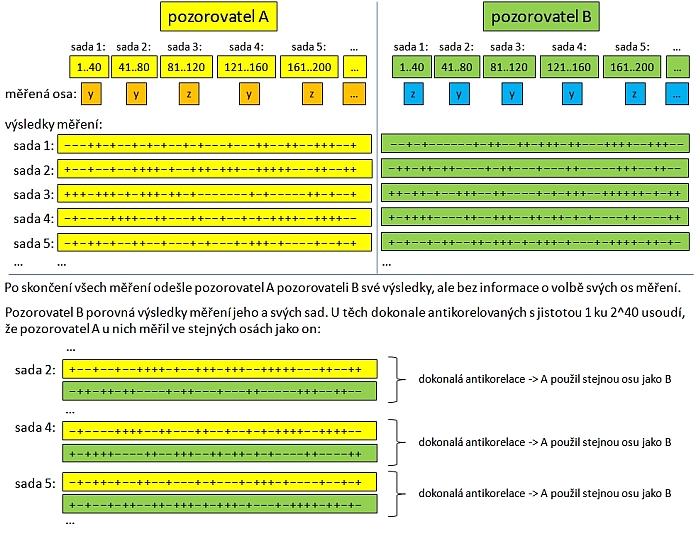
Vliv volby vzdálených měření na korelaci měřených hodnot. Dva pozorovatelé provádějí měření průmětů spinů částic v dlouhé řadě EPR experimentů, kterou rozdělili do sad po 40 měřeních. Uvnitř každé sady volbu svého měření podle své dohody nemění, na začátku každé sady se ale autonomně a na poslední chvíli rozhodnou, kterou spinovou složku budou měřit. Svá měření zaznamenávají, a po skončení měření všech sad pozorovatel A odešle své výsledky pozorovateli B, ale bez informace o své volbě os pro jednotlivé sady. Pozorovatel B porovná výsledky pro každou sadu zvlášť, a s vysokou jistotou odhalí, u kterých sad měřil pozorovatel A ve stejných osách, jako on sám.
To, co je na tomto výsledku z klasického pohledu podezřelé, je právě ten „vznik“ antikorelace u těch sad, kde oba pozorovatelé použili stejnou osu pro měření průmětu spinu. Své rozhodnutí totiž dělají ve stejný okamžik a mohou být od sebe i velice vzdáleni, takže obě části systému se nemohou nijak „domluvit“, pokud by přitom měly respektovat rychlost světla jakožto maximální rychlost. Přesto všechno tyto záhadně vznikající a mizející antikorelace nemohou být nijak použity pro přenos informace nadsvětelnou rychlostí, protože mohou být prokázány až poté, co pozorovatel B dostane od pozorovatele A jeho výsledky klasickou cestou, tedy maximálně světelnou rychlostí. Do té doby drží pozorovatel B v ruce pouze náhodnou sekvenci dat, z níž samotné nemůže žádnou informaci vyčíst.
(Kredit: autor)
Pozorovatel B sice pozná, u kterých sad použil pozorovatel A stejné osy, ale pozná to až poté, co mu A odešle své výsledky měření. Teprve potom je může porovnat se svými a antikorelované sady identifikovat. Do té doby, než mu výsledky od pozorovatele A dorazí, má v ruce jenom náhodnou řadu dat, ze kterých nemá šanci žádnou informaci vyčíst. To podivné na celé té věci je, že to, zda bude ta která sada antikorelovaná či ne, rozhodnou svou volbou pozorovatelé ve stejný čas, ale přitom mohou být velice vzdáleni. Klasická fyzika takový výsledek nepřipouští, protože jedna z oddělených částí systému nestihne „dát vědět“ té druhé části o změněné konfiguraci měřicího přístroje žádnou interakcí na pozadí, pokud je tato interakce přenášena maximálně rychlostí světla. Přesto všechno spor se speciální teorií relativity nemůže vzniknout, protože přes tuto podivnost nelze zmíněné antikorelace žádným způsobem využít k přenosu informace nadsvětelnou rychlostí. Pozorovatel B musí totiž nejprve počkat, až mu klasickou cestou dojdou data zaznamenaná pozorovatelem A, a teprve ta mu poslouží jako klíč k rozšifrování chování pozorovatele A.
Je to zkrátka a dobře náhodnost, která v případě tzv. EPR paradoxu zachraňuje zadek speciální teorii relativity a jejímu světelnému rychlostnímu limitu na přenos informace. Anebo jinak řečeno, náhodnost je to, co umožňuje oběma teoriím, kvantové teorii i speciální teorii relativity, aby spolu koexistovaly bez logických rozporů.
Přesto všechno nebyl Albert Einstein s podobou kvantové teorie spokojen. Mimochodem, EPR paradox nebyl jeho prvním ani posledním pokusem o zpochybnění kvantové teorie, první adresoval už v roce 1927 během páté Solvayské fyzikální konference, druhý pak v roce 1930, a v obou případech se Niels Bohr musel obrazně řečeno docela zapotit, než se mu podařilo Einsteinovy sofistikované argumenty vyvrátit. EPR paradox vzniklý v roce 1935 byl třetím takovým Einsteinovým pokusem, a na rozdíl od jeho dvou předchozích, kdy Bohr nakonec triumfoval, tento skončil jakýmsi patem – Einsteinovi se sice podařilo zkonstruovat myšlenkový experiment, na němž Bohr na rozdíl od předchozích dvou případů nenalezl žádné chyby v předpokladech, oba fyzikální velikáni se ale rozešli v tom, jestli je či není možné výsledek EPR experimentu považovat za akceptovatelný. V té době navíc neexistovala žádná realistická možnost, jak spor experimentálně rozsoudit.
Historická vsuvka:

V debatě Bohra a Einsteina vystupoval Bohr jako velice zdatný advokát kvantové teorie, ve skutečnosti ale Einsteinovi na kvantové teorii nejvíce vadil Heisenbergův princip neurčitosti. Připomeňme, že právě ten ovlivňuje jednu ze dvou klíčových vlastností spinu, kterou je právě nekompatibilita měření průmětů spinu v různých osách, a ta se v EPR experimentu zase odráží v antikorelacích při měření ve stejných osách, případně v nulové korelaci při měření v na sebe kolmých osách. Einstein se s Heisenbergovým principem neurčitosti nikdy nesmířil, podle něj byl znakem neúplnosti kvantové teorie, která by měla být nahrazena nějakou úplnou teorií, ve které by princip neurčitosti neměl místo. Přesto mezi Einsteinem i Heisenbergem vládl velice korektní vztah naplněný vzájemným respektem, a to navzdory dramatickým momentům, které poznamenaly jejich setkání. Heisenberg už jako gymnazista nadšeně hltal Einsteinovy články o speciální teorii relativity, a velice stál o to, aby byl o generaci starším Einsteinem uznán. Heisenberg byl svým způsobem zázračné dítě, doktorát získal ve 22 letech a habilitoval o rok později. Jeho podíl na vzniku moderní kvantové teorie lze jen těžko přecenit - tzv. starou kvantovou teorii, což byla jen klasická mechanika doplněná o pár nesystémových výběrových pravidel pro odůvodnění existence diskrétních energetických hladin atomu, nahradil jím vytvořenou tzv. maticovou mechanikou, díky které objevil existenci nekompatibilních proměnných a došel i ke svému slavnému principu neurčitosti. Stál také za mnoha průlomovými pracemi v atomové a zvláště jaderné fyzice, poprvé správně popsal podstatu feromagnetismu, položil základy relativistické kvantové teorie pole, což je teoretický rámec pro popis elementárních částic včetně procesů jejich kreace a anihilace, dále úspěšně popsal procesy absorpce světla atomy a jeho vyzařování, a výčet jeho vědeckých úspěchů by takhle mohl ještě dlouho pokračovat. Své teorie a nápady posílal Einsteinovi, který se k nim ovšem stavěl čím dál tím více rezervovaně, protože se více a více vzdalovaly od jeho vlastního pojetí fyziky. V roce 1922 se měli poprvé setkat na fyzikální konferenci v Lipsku, ale všechno dopadlo jinak. Při vstupu do konference byl Heisenbergovi vnucen nenávistný pamflet proti Einsteinovi, podepsán německým nositelem Nobelovy ceny Philippem Lenardem a osmnácti dalšími německými vědci. Krátce předtím byl nacistickým komandem zavražděn Einsteinův blízký přítel, německý ministr zahraničí Walther Rathenau, a Albert Einstein figuroval na zveřejněném seznamu budoucích židovských obětí tohoto komanda, proto svou účast na konferenci okamžitě zrušil. Tehdy 21 letý Heisenberg prý byl otřesen takovýmto politickým útokem, nicméně odvahu k jeho veřejnému odsouzení nenašel on, ale jeho o generaci starší přítel Max von Laue, který si dokázal udržet svůj odvážný postoj i mnohem později, ve velice nebezpečných dobách vlády nacistů. Přesto všechno Einstein s Heisenbergem nadále korespondoval, a ačkoliv s ním ve svých odpovědích čím dál více nesouhlasil, navrhl jej dokonce v roce 1928 na Nobelovu cenu za fyziku, kterou o čtyři roky později nakonec Heisenberg dostal. Proti Heisenbergovi byla od roku 1933 vedena nenávistná kampaň, která vyvrcholila v roce 1937 jeho nařčením mj. z „židovského myšlení“ v oficiálním žurnálu SS. Po takových útocích většinou následovala návštěva pánů v kožených kabátech, a dotyčného nešťastníka pak už kolikrát nikdo nikdy nespatřil. Takovému konci zamezila návštěva Heisenbergovy maminky u matky Heinricha Himmlera, jelikož se obě znaly přes Heisenbergova pradědečka a Himmlerova dědečka, oba kamarády z turistického klubu. Himmler následně poslal jeden dopis Reinhardu Heydrichovi, ve kterém napsal, že Německo si nemůže dovolit ztratit Heisenberga, protože pro ně může být užitečný. Ve druhém dopise poslaném Heisenbergovi mu radil, že musí umět oddělovat profesionální znalosti jiných vědců od jejich osobních a politických postojů. O pár let později bylo na Heisenberga vzpomenuto v souvislosti se zahájením nacistického projektu na výrobu atomové zbraně, a Heisenberg se nezpěčoval – ale to už je jiný příběh.
Bohrova a Einsteinova debata rozpoutala rozsáhlou diskuzi v celé fyzikální komunitě, přičemž závěry obou fyziků byly vydestilovány do podoby několika málo principů, kterým měla každá akceptovatelná fyzikální teorie podle Einsteina vyhovovat, zatímco kvantová teorie jim nevyhovovala. Jednalo se zejména o tzv. princip realismu a princip lokality.
Princip realismu požaduje, aby každé měřitelné veličině, tedy i spinu částic, odpovídalo „něco skutečného“, co existuje nezávisle na měření. Výsledek každého měření by tedy měl být dán už před samotným měřením, a např. volba měřené pozorovatelné by ho neměla narušit. Je evidentní, že už tento samotný požadavek není slučitelný s Heisenbergovým principem neurčitosti, který tvrdí, že měření jedněch veličin ovlivní neurčitost měření jiných, s nimi nekompatibilních veličin.
Princip lokality potom požaduje, že pokud jsou dvě části systému separovány, jako např. elektron a pozitron poté, co se dostatečně vzdálí z místa svého zrodu, tak potom měření na jednom z nich nijak nesmí ovlivnit stav druhé, vzdálené části systému.
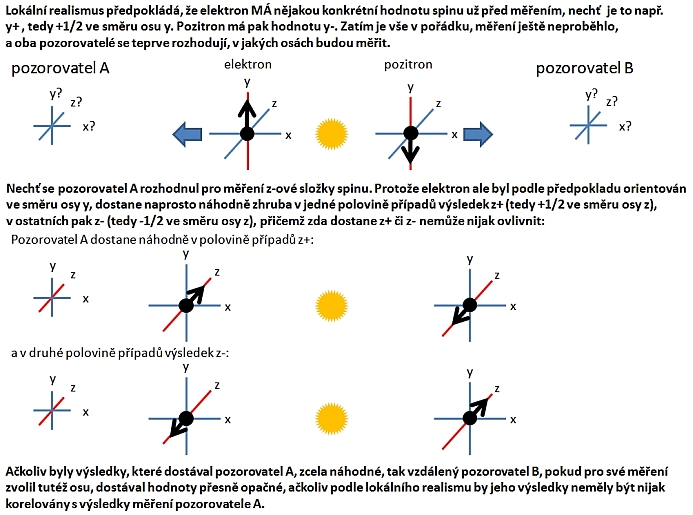
Konflikt EPR experimentu s lokálním realismem.
Protože jsou výsledky měření v osách kolmých na směr spinu dokonale náhodné, tak je podle klasické teorie nevysvětlitelné, jak může vzdálený pozorovatel B, pokud měří ve stejné ose, dostávat 100% antikorelaci s výsledky pozorovatele A. Kredit: autor
Fyzikální komunita se následně rozštěpila na přívržence kvantové teorie v její stávající podobě, a na přívržence různých lokálně realistických alternativ ke kvantové teorii, jako byly např. modely s tzv. skrytými proměnnými. Druhá skupina prohlašovala, že kvantová teorie je neúplná, a že např. Heisenbergův princip neurčitosti je pouhý důsledek toho, že neznáme hodnoty nějakých dnes skrytých proměnných, které mohou být měřením nechtěně ovlivněny a které mohou v důsledku změnit dynamiku systému tak, že se efektivně chová právě tak nepochopitelně, jak to kvantová teorie předpovídá.
Dlužno ovšem říct, že většina kvantových fyziků si s principy stojícími v základech kvantové teorie hlavu zase až tak moc nelámala, a věnovala se raději praktickým aplikacím kvantové teorie, které přibývaly jako houby po dešti. Kvantová teorie se v té době stala nezastavitelným parním válcem (který se mimochodem dodnes nezastavil), který úspěšně projel mnoha obory fyziky i chemie. Denně přibývaly další její úspěšné aplikace nejen v teorii elementárních částic a v jaderné a atomové fyzice, ale také ve fyzice pevných látek, při popisu supravodivosti, supratekutosti, ale i obyčejné elektrické vodivosti, při popisu polovodičů, ve spektroskopii, kvantové chemii, elektronice, laserové fyzice, krystalografii, fotonice, a tak by se dalo pokračovat dlouho. Proč se tedy mořit s abstraktními aspekty kvantové teorie, když výzkum denně ukazuje neuvěřitelnou předpovědní sílu kvantové teorie?
Uplynula další skoro tři desetiletí, než se spíše filosofickou rozepři Bohra a Einsteina podařilo přeformuloval do podoby experimentu, který by umožnil testovat dokonce ony dva zmíněné základní principy realismu a lokality. V roce 1964 se to podařilo Johnu Stewartu Bellovi, severoirskému fyzikovi. Bell matematicky exaktně dokázal, že jakákoliv teorie, která současně respektuje princip lokálnosti a princip realismu, musí vyhovovat jistým speciálním nerovnostem, které dnes nesou jeho jméno.
Bellovy nerovnosti se týkají maximálních hodnot jednoho výrazu, který je šikovně zkonstruován z korelačních funkcí výsledků měření provedeného na dvou oddělených místech. Lokálně realistické teorie dávají pro tento výraz jako jeho maximální hodnotu číslo 2, ale pro kvantovou teorii se dá ukázat, že v optimálně zvolených případech lze docílit až hodnoty odmocnina(2) krát větší, tedy zhruba 2,828. Pokud by pro tyto optimálně zvolené případy experiment dal hodnotu 2,828, tak by to sice ještě neznamenalo, že kvantová teorie je správná, nicméně spolehlivě by to pohřbilo všechny lokálně realistické teorie, protože z premis lokálního realismu plyne limit 2 matematicky exaktně. Je to podobné, jako kdyby podle zvolených premis měla být nějaká hodnota třeba kosinem nějakého úhlu, ale její měření by dalo výsledek 1,3; nevyhnutelný závěr by byl, že výchozí premisa byla nutně špatně, protože kosinus žádného úhlu nemůže být větší než jedna.
Nerovnosti jsou ve své konkrétní podobě formulovány pro limitní hodnotu 2, tzn. že lokálně realistické teorie je nikdy nenarušují, kvantová teorie je ale narušuje v těch případech, ve kterých předpovídá hodnotu Bellova výrazu větší než 2. Narušení Bellových nerovností je tedy synonymem pro pohřeb lokálního realismu. Zbývá tedy už jen proměřit hodnotu Bellova výrazu v oněch rozhodujících případech, a tím i rozhodnout dávný spor Einsteina a Bohra.
Mohlo by se zdát, že odlišit experimentálně hodnotu 2 od 2,828 by neměl být takový problém. Ve skutečnosti to ale trvalo dalších dlouhých několik desítek let, než se experimentální technika dostala na takovou úroveň, aby Bellův test bylo možné provést. Problém je totiž v tom, že právě ty experimentální situace, pro které vychází hodnota Bellova výrazu jako větší než 2, jsou velice obtížně realizovatelné. Jsou k nim totiž potřeba tzv. entanglované čili provázané páry částic, přičemž navíc částice z každého takového páru musí být od dostatečně vzdálené – a především toto je velikým kamenem úrazu.
Jeden případ entanglementu jsme si už výše popsali, byl to právě onen elektron-pozitronový pár, který figuroval v myšlenkovém EPR experimentu. Pro praktické měření se ale entanglované elektron-pozitronové páry ani trochu nehodí, už jen kvůli tomu, že pozitron by v procesu měření velice ochotně anihiloval s prvním elektronem, na který by natrefil. Existuje ale možnost využít i jiné entanglované páry, např. dva elektrony nebo dva fotony. Dokonce lze entanglovat i spiny jader atomů sedících v uzlech krystalické mřížky, anebo spiny iontů lapených v uzlech „optických krystalů“, tedy uměle vytvořených mříží z laserových paprsků. Experimentátoři zabývající se entanglementem nejvíce milují pracovat s fotonovými páry, a to proto, že se jednoduše připravují, a navíc mají fotony další příjemnou vlastnost, v opticky průhledných prostředích interagují velice zanedbatelně (proto jsou také tato prostředí průhledná, naopak prostředí, se kterými fotony reagují významně, jsou buď neprůhledná anebo pouze průsvitná), a díky tomu si své vlastnosti uchovávají relativně dlouho nedotčené, takže jsou přístupné následnému měření. Navíc se fotony dají dobře posílat optickými vlákny, díky čemuž je experimentátoři snadno mohou nasměrovat přesně kam potřebují. V některých případech je ale naopak lepší pracovat s elektrony, protože fotony, jak známo, stále někam pospíchají a zastavit se je podaří pouze jejich absorpcí v látce, což pro ně znamená konečnou stanici na jejich celoživotní pouti. Oproti tomu elektron umí celkem spořádaně sedět buďto v nějaké krystalové vakanci, nebo v nějaké z mnohých rafinovaných pastí, a je ochoten snášet příkoří opakovaných měření, už jen proto, že částečnou diplomatickou imunitu bránící jeho snadnému zničení mu garantuje zákon zachování elektrického náboje.
Je nutné zmínit, že ne u každého měření prováděného na entanglovaných párech budou Bellovy nerovnosti narušeny. Tak např. nebudou narušeny v žádném z případů ilustrovaných výše, kdy pozorovatelé provádí měření buďto ve stejných osách, anebo v navzájem kolmých osách, a proto analýzou těchto situací nelze exaktně rozhodnout mezi kvantovou teorií a lokálně realistickými teoriemi (dá se ukázat, že v případech pospaných výše vyjde hodnota Bellova výrazu přesně 2). To se vzhledem k popsaným vlastnostem EPR experimentu může zdát zvláštní, vždyť jsme přece celou dobu tvrdili, že EPR experiment odporuje klasické fyzikální intuici, která v některých případech neumí vysvětlit antikorelaci vzdálených měření. Bellův vztah ale není o nějaké intuici, Bellův vztah je matematicky exaktně dokázaným vztahem plynoucím z exaktně formulovaných předpokladů. Jde tedy o situaci vzdáleně podobnou tomu, jako když nebylo možno usvědčit Al Caponeho ze zločinů, za nimiž nade vši pochybnost stál, ale podařilo se ho dostat za prokázané krácení daní, za což byl nakonec také odsouzen. Jinými slovy, zatím jsme si sice mohli celou dobu říkat, že výsledky EPR paradoxu jsou z hlediska klasické fyziky divné či krajně podezřelé, nicméně teprve až narušení Bellových nerovností je tím korunním důkazem, který prokazuje neplatnost lokálního realismu jako takového.
Nebudeme zde zabíhat do matematického rozboru Bellových nerovností, vystačme si pouze s tím, že jejich analýzou se dá ukázat, že maximální odchylka od klasického chování nastane tehdy, když pozorovatel B měří v osách o 45 stupňů pootočených vůči osám pozorovatele A. Přitom pozorovatel A provádí měření ve dvou různých polohách svých os, navzájem na sebe kolmých, a pozorovatel B také měří ve dvou různých na sebe kolmých polohách, které jsou ale o 45 stupňů pootočené vůči osám pozorovatele A. Celkem tedy existují čtyři kombinace volby os měření, jak ukazuje následující obrázek.
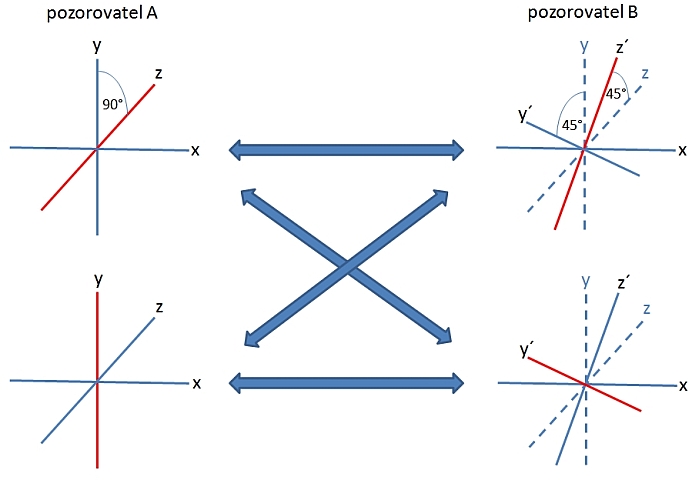
Volby měřených os potřebné pro testování Bellových nerovností.
Pozorovatel A měří ve dvou na sebe kolmých osách, např. y a z. Pozorovatel B měří také ve dvou na sebe kolmých osách, ty ale musí být pootočeny o 45 stupňů vůči osám použitým pozorovatelem A. Teprve tehdy se maximalizuje hodnota Bellova výrazu počítaného z korelací jednotlivých měření (pootočené osy jsou označené y´ a z´). Celkem existují 4 kombinace voleb os obou pozorovatelů. (Kredit: autor)
Provede se dostatečně dlouhá řada měření pro každou ze čtyř kombinací měřených os, a pro každou z těchto kombinací se spočte odpovídající korelační funkce ze získaných četností naměřených průmětů obou spinů. Pro každé nastavení os lze dostat celkem čtyři možné kombinace výsledků, tak např. pro volbu os z a z´ jsou to kombinace [z+;z´+], [z+;z´-], [z-;z´+], [z-;z´-] (celkem tedy existuje 16 různých variant nastavení měřených os a získaných výsledků). Ze čtyř korelačních funkcí se pak vypočte onen klíčový výraz, jehož hodnota pak rozhodne, jestli byly či nebyly Bellovy nerovnosti narušeny.
Dřívější testování Bellových nerovností sice už celkem spolehlivě prokázalo jejich narušení, přesto ale ponechávalo aspoň malilinkou naději přívržencům lokálního realismu. Vždycky totiž zbyla nějaká skulina, která mohla být využita, i když spíše jako zoufalý protiargument než jako seriózní zpochybnění výsledků testování. Jedna z typických těžkostí při testování s použitím entanglovaných fotonů byla nedostatečná účinnost detektorů, které v některých případech foton nezaznamenaly. Nejde přitom o nic záhadného, protože reálné detektory nikdy nemají stoprocentní účinnost, a jejich občasné selhávání je naprosto náhodným statistickým procesem. Proto by mělo být naprosto akceptovatelným postupem, když se do výsledků zahrnou pouze případy, kdy detektory neselhaly, protože se neočekává zlomyslnost typu, že detektor selhává jen v těch případech, které by i tak jen s odřenýma ušima tak tak stihly zachraňovat lokální realismus. Přesto mohli přívrženci lokálního realismu formálně argumentovat, že taková možnost hypoteticky existuje.
Tato mezera byla postupně zacelena s postupujícím zlepšováním účinnosti detektorů. V odpovídajících testech byla ale zase přítomna jiná formální mezera, a to ta, že měření nebylo dostatečně rychlé, takže v principu bylo možné, aby informace z jednoho detektoru došla do druhého rychlostí světla a postarala se o synchronizaci výsledků jich obou. Ani tato varianta nebyla brána zas až tak vážně, protože oddělené části systému byly navzájem dobře izolované - případná synchronizace by tedy musela probíhat prostřednictvím nějaké neznámé interakce, která by nepozorovaně prošla zmíněnými izolacemi, a přitom spolehlivě „našla“ svůj protějšek, se kterým by se následně spikla tak, aby Bellovy nerovnosti vyšly narušené. Tato mezera byla zacelena zase jinými testy, které ale pro změnu zase nedisponovaly dostatečně účinnými detektory.
Výsledky všech těchto předchozích testů ale i tak dost přesvědčivě vypovídaly o narušení Bellových nerovností, a pro přívržence lokálně realistických teorií už zbývalo jenom poslední stéblo naděje, kterého se zoufale chytali. A toto stéblo Ronald Hanson se svým delftským týmem definitivně přetnul jejich experimentem, ve kterém poprvé odstranil obě formální mezery zároveň, tedy jak mezeru působenou nedokonalostí detektorů, tak tu související s požadovanou rychlostí měření.
O delftském experimentu už dostatečně referoval předchozí článek „Kvantová mechanika opět poráží Einsteina a jeho lokální realismus“ od Stanislava Mihulky, nemá proto smysl zde opakovat tam už zmíněné informace, proto zde zmíním jen pár dodatečných detailů. Hanson a spol. použili pro své měření elektrony uvězněné v defektech dvou krystalů diamantu vzdálených od sebe 1,3 km. Protože pro testování Bellových nerovností je nevyhnutelné pracovat s entanglovanými částicemi, tak bylo nutné vzdálené elektrony před zahájením experimentu provázat, což se provedlo s využitím tzv. přenosu entanglementu, kdy se vzdálené částice nejprve provážou s fotony, a tyto fotony se pošlou optickým vláknem na polopropustné zrcadlo, na kterém se pro změnu provážou ony. Dá se ukázat, že tímto způsobem dojde k provázání i původních elektronů úplně stejně dobře, jako by bylo možné je provázat jejich bezprostřední interakcí bez účasti fotonů. V praxi se proto s oblibou používá právě tento způsob přenosu entanglementu, protože entanglement elektronů je záležitost extrémně křehká a při posílání entanglovaných elektronů na jejich vzdálená místa by se s velkou pravděpodobností „rozbil“ (zatímco fotony, jak bylo už zmíněno výše, s tímto problém nemají).
Několik málo mikrosekund po provázání elektronů ve vzdálených krystalech se v tentýž okamžik provede jedno ze zmíněných měření, spočívající ve výběru osy a v následném měření průmětu spinu do této osy. Výběr osy byl svěřen do péče pro ten účel extrémně rychlému generátoru náhodných čísel, který musel umět dostatečně rychle udělat rozhodnutí o tom, která osa se bude měřit (konkrétně musel umět dostatečně rychle vygenerovat náhodné číslo, na jehož základě byl změřen průmět do té které osy). Výsledek tohoto měření byl záznamovým zařízením zaregistrován dříve, než by světlo stihlo dorazit k druhému krystalu, pokud by od prvého krystalu vyrazilo v okamžiku, kdy byla generátorem vybrána měřená osa, díky čemuž byla eliminována hypotetická „rychlostní“ mezera.
Po provedení 245 měření byla získána hodnota výrazu figurujícího v Bellových nerovnostech jako 2,42 se standardní odchylkou 0,2, tedy hodnota dostatečně převyšující maximální hodnotu 2 přípustnou pro lokálně realistické teorie. Tato hodnota je nižší než maximálně přípustná hodnota, kterou povoluje kvantová teorie, a která činí 2,828, kterýžto rozdíl je způsoben jednak ne úplně stoprocentní účinností detektorů (ta se pohybovala kolem 90%), a jednak ne úplně dokonalým entanglementem elektronů (tzv. „přesnost“ – anglicky fidelity – entanglovaného stavu byla 92%).
Delftský experiment tedy definitivně uzavřel více než 80 let starou debatu o podstatě kvantové teorie. Tento experiment neříká, a z principu ani nemůže říct, že kvantová teorie je správnou teorií. Říká ale, že neexistuje žádná alternativní teorie, která by vyhovovala principům lokality a realismu, tak jak požadovali Albert Einstein i mnozí jiní vědci, kteří se nehodlali smířit s podivnými nelokálními korelacemi, které kvantová teorie předpovídá. Tyto nelokální kvantové korelace jsou ve skutečnosti už léta předmětem zkoumání v moderních fyzikálních směrech, jakými jsou výzkum kvantové kryptografie, kvantové teleportace anebo kvantového computingu, ve kterých se rýsuje fascinující potenciál budoucího možného využití především výše zmíněných entanglovaných stavů, ale nejen jich – ale to už by byl zase jiný příběh.
Psáno pro osel.cz
Reference:
Historic Delft Experiments tests Einstein's 'God does not play dice' using quantum 'dice'
Quantum Science and Technology in Diamond
The universe really is weird, and a landmark quantum experiment proves it
EPR paradox
Stern–Gerlach experiment
Spin quantum number
Uncertainty principle
Bohr–Einstein debates
Werner Heisenberg and Albert Einstein
Principle of locality
Bell's theorem
Kvantová mechanika opět poráží Einsteina a jeho lokální realismus
Autor: Stanislav Mihulka (28.10.2015)
Diskuze:
hmmm
Jaroslav Řezník,2015-11-10 20:44:08
Mluví se o tom, že vlastně zeorie relativity nebyla narušena, že rychlost světla nebyla překonána, že není možné přenášet informace nadsvětelnou rychlostí. Že z dat na druhé straně nelze nic vyčíst, že je nutné je porovnat a to je velice klasicky pomalé. Že prostě musí přijít ke slovu vědomí
Nemluví snad spousta kvantových fyziků o roli vědomí. Co když je vědomí jakési podloží vesmíru a je všude. Třeba má různou hustotu - víc je ho u člověka než u stromu či brouka či kamene. Vědomí nemusí být myšlení ale jakési podloží myšlení, emocí, ega, atd. Ten pokus se štěrbinama je docela šokující.
Pokud je vědomí součástí systému, pak už to tak nelogicky nezní. Kvantovka přeci tvrdí na základě různých paradoxů, že po pozorování, uvědoměmí nastává jaksi kolaps historie jiných možností. Kolaps minulosti nebo větve minulosti
Re: hmmm
Richard Palkovac,2015-11-10 21:05:32
Na 100 % si mozete byt isty iba jedinou objektivne existujucou "vecou" a tou je Vase vedomie.
Pavel Ulsky,2015-11-06 00:57:04
Co když se 2 provázané částice nějakým způsobem stejně roztočí. Spin (magnetický moment?) rotuje stále stejnou rychlostí pro obě částice. fáze jedné částice je ale o polovinu otáčky posunuta. Při měření se spiny změří ve stejný okamžik. Tzn. naměříme +1/2 na jedné částici i -1/2 na druhé, obě se tím zastaví, takže měříme opakovaně stejné hodnoty. Nevysvětlovalo by to záhadné působení na dálku? Co když prostě žádné není, jen se ty provázané částice chovají od začátku stejně a tím, že je měříme "ve stejný okamžik" naměříme takové hodnoty. Tzn. o opačném spinu není rozhodnuto v době měření, ale už na začátku při provázání částic.
Re:
Richard Palkovac,2015-11-09 08:12:59
Zahadne posobenie na dialku to vobec nevysvetluje, nakolko to zahadne pozobenie nie je v tom, ze my nameriame na druhej castici opacny spin, ale v tom ako rychlo sa "informacia" o zastaveni "tocenia" spinu prenesie k druhej castici a prave to je ten problem, ze to vyzera tak, ze sa to prenesie okamzite.
Presne podobny myslienkovy pochod ako Vas , napadol aj mna. Vysvetlit to, ze stale prvy pozorovatel nameria nahodnu hodnotu spinu pri prvom merani povedzme v osi "z" by sa dalo celkom jednoducho, tym "tocenim". Pri generovani castic sa spiny "roztocia" a pokial by sme poznali funkciu "tocenia sa" v case a mali by sme presny casovas pre moment merania, mohli by sme dopredu vediet, aky spin v danej osi nameriame. Problem je ale v tom presnom case merania, lebo chyba nasho casovaca by bola stale vacsia ako Planckov cas. A prave to je dovod, myslim si, preco nameriame vzdy nahodnu hodnotu.
Ak by sme dalej predpokladali, ze spim sa "otoci" prave za Planckov cas, tak by sme mali aj vysvetlenie preco nameriame na druhej castici spin opacny. To ale vobec nie je podstatne.
Podstatny je totiz moment "zastavenia spinu". A prave ten sa prenasa okamzite.
Re: Re:
Richard Palkovac,2015-11-09 08:17:29
upresnenie vyjadrenia :
moment "zastavenia spinu" = casovy moment "zastavenia spinu"
Re: Re:
Pavel Ulsky,2015-11-09 22:04:45
>> nakolko to zahadne pozobenie nie je v tom, ze my nameriame na druhej castici opacny spin, ale v tom ako rychlo sa "informacia" o zastaveni "tocenia" spinu prenesie k druhej
Ano o to mi šlo v prvé řadě. Může to být klidně tak, že se částice jen synchronizují, a pak na obou naměříme stejné hodnoty (s opačným znaménkem). Ve skutečnosti se nic nepřenáší, takže to nemusí být ani žádná záhada.
Re: Re: Re:
Richard Palkovac,2015-11-10 09:47:50
No, zahada to prave ze je, lebo aj ked su tie castice zosynchronizovane, ako vie ta druha (ktora je mozno na Marse) okamzite, ze kedy ma zastavit "otacanie svojho spinu" ?
Mozno si predstavujete nejaku synchronizaciu, mechanizmus ktorej je nam neznamy.
Klasicku synchronizaciu si mozeme predstavit napriklad cez ocelovu hriadel. Na jej koncoch su dva kolesa a tie sa otacaju synchronne. Laik by si myslel, ze ked jedno koleso pribrzdime,tak to druhe sa tiez okamzite pribrzdi. Ale uz aj znaly technik vie, ze ta hriadel nie je absolutne pevna (ma urcitu pruznost) a to druhe koleso sa zacne spomalovat az po urcitom zlomku sekundy. Fyzik, ten vie ze to bude vzdy kusok pozdejsie ako tam na druhy koniec dorazi svetlo, presnejsie povedane fotonova interakcia.
Takze ta synchronizacia castic, musi byt nejaky nam neznamy princip, ak fyzici nepodvadzaju vo svojich experimentoch (dufam ze nie).
Re:
Pavel Brož,2015-11-09 19:17:22
Spin není projevem točení se částice, je projevem toho, že vlnová funkce popisující částici má dvě nebo více nezávislých komponent. V případě elementárních fermionů to jsou dvě komponenty (ve skutečnosti čtyři, ale dvě korespondují s popisem částice a zbylé dvě s popisem příslušné antičástice), v případě fotonů a gluonů jsou tam čtyři komponenty, ale jen dvě jsou fyzikálně nezávislé (zbylé dvě se dají eliminovat volbou tzv. kalibrace), v případě hmotných intermediálních bozonů jsou to tři. Je-li navíc částice elektricky nabitá, pak se dá ukázat, že z odpovídající dynamické rovnice (což je Diracova rovnice pro elektron, pro intermediální nabité bozony je to tzv. Procova rovnice) pak vyplyne velikost poměru mezi spinem a magnetickým momentem částice.
Není k tomu potřeba žádná představa točící se částice, dalo by se říci, že taková představa je nadbytečná úplně stejně, jako se pro speciálně relativistickou dynamiku ukázala nadbytečná hypotéza éteru. Ba dokonce tato představa koliduje s dalšími teoriemi. Dá se např. ukázat, že aby mohl být spin vysvětlen pomocí rotace elektronu, musel by elektron rotovat na svém obvodu rychlostí větší, než rychlost světla. Nevíme sice, jak je elektron velký (současná data dokonce neprotiřečí představě, že je bodový, rozptylová data ze srážek při těch největších energiích umožňují položit vrchní limit na nebodovost elektronu řádově někam k 10^-18 metrů), nicméně víme, že i kdyby byl maximálně tak velký, jak připouští experiment, musel by rotovat na obvodu rychleji než světlo. To by samo o sobě nemusel být problém, jenže ona navíc z představy rotujícího elektronu vychází i jiná než skutečná hodnota poměru mezi magnetickým momentem elektronu a jeho momentem hybnosti - skutečný poměr je totiž více než dvojnásobný. To už je problém mnohem podstatnější, protože nad nadsvětelnou rychlostí rotace elektronu můžeme mávnout rukou jako nad něčím, co stejně neumíme měřit, kdežto poměr magnetického momentu elektronu a jeho spinu umíme měřit velice přesně.
Takže spin se s rotací elektronu nespojuje. Elektron dnes popisujeme v rámci standardního modelu jako bodovou bezrozměrnou částici, kteréžto představě dodnes žádná experimentální data neprotiřečí. V rámci tzv. superstrunových teorií je sice elektron popsán nikoliv bodově, ale jako struna nulové tloušťky a délky srovnatelné s Planckovou délkou, ta je řádově 10^-34 metrů, tedy dokonce ještě 16 řádů pod dnešním experimentálním limitem. Ale ani v teorii superstrun není spin důsledkem nějaké rotace té struny, ale stejně jako ve standardním modelu plyne z dynamických rovnic, které zároveň pro nabité částice dávají správnou hodnotu jejich magnetického momentu, ne tu, kterou bychom dostali z představy rotující nabité částice.
Re: Re:
Pavel Ulsky,2015-11-09 22:27:34
Díky, za vysvětlení.
Představuji si to takto: Spinový magnetický moment jedné částice, který se mění nezávisle na druhé částici se propojením synchronizuje. Tzn. určí se jakoby volná proměnná. Spinový magnetický moment se pak bude měnit synchronně u obou částic. Ať je dáme jakkoli od sebe, tak při současném měření (prodleva menší než možný přenos informace) naměříme stejnou hodnotu jen s opačným znaménkem. Tzn. nic se nepřenáší, stejnost výsledku už je určena sesynchronizovaním částic dohromady - provázáním, ne tím, že se magicky přenese nějaká informace o jednom pření na druhé.
Nezáleží na transformaci, nemusí se nic točit. Možná bylo lepší nazvat to "změna" místo "točení".
Re: Re: Re:
Richard Palkovac,2015-11-10 11:42:30
Samozrejme ze spin nie je fyzicke tocenie sa castice, to je jasne, ale ako pomocka pre pochopenie toho, ze preco je kvantove prepojenie castic zahada, je to dobre.
Re: Re: Re:
Pavel Brož,2015-11-10 21:11:27
Takhle, tam jde o to, z čeho vyjdeme. Buďto předpokládáme, že platí premisy kvantové mechaniky, mezi něž mj. patří principiální náhodnost při získávání výsledků nějaké veličiny v obecném stavu. Potom nám musí přijít divné, stejně jako Einsteinovi, že vzdálené měření umožňuje dávat přesné antikorelace, když přece výsledky měření jsou náhodné. Anebo odmítneme některé (nebo i všechny) premisy kvantové teorie, např. zrovna tu, že měření je zcela náhodné, a vymyslíme nějaký klasický model, který ty vzdálené korelace vysvětluje. A tady právě zaúřadují Bellovy nerovnosti, které poskytují limit na jeden speciální výraz zkonstruovaný z korelačních funkcí. Bellovy nerovnosti na základě velmi obecného předpokladu ukazují, jakou maximální hodnotu toho výrazu dává libovolná klasická teorie. Tím předpokladem je, aby měření na jednom místě nemohlo být ovlivněno měřením na vzdáleném místě.
Mezi vznikem EPR paradoxu a odvozením Bellových nerovností uběhlo téměř třicet let. Během této doby vzniklo spoustu klasických modelů vysvětlujících tu synchronizaci, podobně jako to vysvětlujete Vy, a v principu se nedalo nijak rozhodnout, jestli jsou správně tyto modely nebo kvantová teorie. Až Bellovy nerovnosti přinesly změnu, protože přišly s kvantifikovatelným výrazem, jehož hodnota se aspoň v principu dala měřit a na základě ní se daly event. daly vyřadit některé teorie – dokonce celá třída teorií, teorií lokálně realistických. Teprve od tohoto okamžiku to začalo být opravdu zajímavé, protože do té doby se dalo vymyslet hodně zajímavých klasických mechanismů, které by EPR paradox vysvětlily.
U Bellových nerovností je zajímavé to, že nejsou porušeny ani když oba pozorovatelé měří ve stejných osách, ani když měří v osách kolmých. Vysvětleme si proč tomu tak je. Pokud totiž pozorovatelé použijí tytéž osy, pak z důvodů zákonu zachování momentu hybnosti musí naměřit přesně opačné hodnoty, tj. dostat antikorelaci. To ale není nic divného ani z pohledu klasické fyziky. Opravdu, pokud by kvantové jevy neexistovaly a spin by byl obyčejným klasickým momentem hybnosti, pak by to ani jinak nešlo – původní stav měl nulový moment, takže jakmile jedna část má nějaký nenulový, druhá nutně musí mít opačný. Takže při použití stejných os nelze žádný nesoulad mezi klasickými a kvantovými teoriemi čekat.
Stejně tak jej ale nelze čekat při použití navzájem kolmých os. V tomto případě dává kvantová teorie nulovou korelaci, což znamená, že hodnoty měřené oběma pozorovateli jsou navzájem naprosto nezávislé. Taková situace ale také není z pohledu klasické fyziky nic zvláštního. Dvě částice mohou být nezávislé a hodnota nějaké veličiny měřené u jedné z nich vůbec nemusí korelovat s hodnotou vzdáleného měření (např. pokud měříme okamžitou rychlost dvou vzdalujících se pylových zrnek, která se v roztoku pohybují Brownovým pohybem). Takže pro případ nulové korelace také máme klasický model, pro něj tedy k vyřazení klasických teorií evidentně dojít nemůže.
Jediná šance, kde bychom mohli očekávat nějakou disproporci, která by umožnila vyloučit jednu ze stran sporu, je tedy měření, kde nedochází ani k úplné (anti)korelaci, ani k nulové korelaci. Ukazuje se, že v případě spinu elektronů je optimálním úhlem 45° (plus násobky 90°), při kterém se maximalizuje rozdíl mezi tím, jakou hodnotu onoho speciálního výrazu dá kvantové teorie, a jakou mohou maximálně dát lokálně realistické teorie. V případě fotonů je to jinak – maximální (anti)korelace nastávají jak při stejných osách, tak pokud jsou na sebe kolmé, a naopak nulová korelace nastává, pokud je mezi nimi úhel 45°. Protože jak víme, pro případ úplných (anti)korelací ani nulových korelací spor získat nelze, tak ani moc nepřekvapí, že největší rozdíl mezi předpověďmi kvantové teorie a jejich lokálně realistických alternativ získáme pro úhel 22,5° (plus násobky 45°).
Takže není problém vymyslet model, který „zdůvodní“ tu „synchronnost“ vzdálených částic, podobně jako se to pokoušíte vysvětlit Vy. To, co je problém, je aby ten model dal korelace vyhovující Bellovým nerovnostem pro úhly os, u kterých nastává největší rozdíl mezi klasickými teoriemi a teorií kvantovou. Bellovy (nebo CHSH) nerovnosti jsou bohužel v tomto ohledu naprosto nesmlouvavé, a říkají, že žádný podobný klasický model neumí dát pro žádný úhel hodnotu větší než 2, zatímco kvantová teorie umí dát u elektronů pro úhel 45° (u fotonů pro úhel 22,5°) hodnotu až 2,828.
Re: Re:
Richard Palkovac,2015-11-10 21:13:03
Este ma napadla jedna vec. Pokial sa po vytvoreni previazanych castic spin len nastavi a nemeni sa az pokym neurobime prve meranie, tak to nie je ziadny zazrak.
Kedze mame len jeden pokus, nie je to mozne vylucit.
Potom ked urobime prve meranie sa uz spin zacne menit, previazanie uz ale neplati.
Existuju vobec dokazy o tom, ze spin sa po vzniku previazanych castic (pokym nenastane prve meranie) meni ?
Alebo je prave toto to einsteinovske chapanie ?
Re: Re: Re:
Pavel Brož,2015-11-11 20:59:14
Takhle, asi nejlepší bude, když porovnáme výsledky, jaké se získají na entanglovaných páru částic, s výsledky, jaké se získají na neentanglovaných párech částic, které přitom mají navzájem opačné spiny. Zpětně si uvědomuji, že jsem ve článku nezdůraznil, že entanglement není jen o tom, že částice mají navzájem opačný spin, takže nyní se to pokusím napravit.
My umíme připravit neentanglované páry částic tak, že přitom mají opačné spiny. Experimentálně je to velice jednoduché udělat, prostě vezmeme dejme tomu 20000 dvojic elektronů, pro každou dvojici necháme každý z elektronů prolétnout Sternovým-Gerlachovým přístrojem, které jsou oba nastaveny, aby měřily ve stejné ose, dejme tomu v ose východozápadní. Dostaneme čtyři skupiny výsledků: ve cca 5000 dvojicích budou mít oba elektrony průmět spinu +1/2, v dalších cca 5000 dvojicích bude mít první elektron průmět +1/2, zatímco druhý -1/2, atd.. Do dalšího experimentování vyberme jenom ty, které mají opačné průměty, takže nám z původních 20000 zbude cca 10000 dvojic, z nichž cca 5000 dvojic bude mít spiny [+1/2;-1/2], zatímco dalších cca 5000 dvojic bude mít spiny [-1/2;+1/2]. Důležité je vědět, že v případě těchto neentanglovaných dvojic ty elektrony po tomto výběru uvedené spiny mají a samy od sebe se nemění. O tom se lze přesvědčit opakovaným měřením ve stejné (tj. východozápadní) ose, kdy všech cca 5000 dvojic, které jsme vybrali se spiny [+1/2;-1/2], dají opět spiny [+1/2;-1/2] (tj. ani jedna z těchto dvojic při opakovaném měření nedá [-1/2;+1/2]), a podobně všech cca 5000 dvojic, které jsme vybrali se spiny [-1/2;+1/2], dají opět spiny [-1/2;+1/2] (tj. ani jedna z těchto dvojic při opakovaném měření nedá [+1/2;-1/2]).
Takže máme 10000 předpřipravených neentanglovaných dvojic, kdy v každé z nich mají ty dvě částice přesně opačný spin. Nyní na nich provedeme měření ve směru kolmém na předchozí osu, např. ve směru severojižním. V neentanglovaných dvojicích jsou elektrony nezávislé, přesně tak, jak očekáváme podle klasické fyziky, takže nepřekvapí, že z 5000 dvojic s „východozápadními“ průměty spinů [+1/2;-1/2] dostaneme po „severojižním“ měření cca 1250 dvojic se „severojižními“ průměty [+1/2;+1/2], dalších cca 1250 bude mít průměty [+1/2;-1/2], dalších cca 1250 bude mít průměty [-1/2;+1/2], a zbylých cca 1250 průměty [-1/2;-1/2]. Analogické výsledky dostaneme pro 5000 dvojic s „východozápadními“ průměty [-1/2;+1/2]. Suma sumárum: z 10000 dvojic předpřipravených z prvního „východozápadního“ měření budeme mít po „severojižním“ měření cca polovinu se shodnými průměty spiny, a druhou polovinu s opačnými průměty spinu. Konkrétně cca 2500 dvojic dopadne se „severojižním“ průmětem [+1/2;+1/2], dalších cca 2500 s průmětem [+1/2;-1/2], dalších cca 2500 s průmětem [-1/2;+1/2], a nakonec posledních cca 2500 dvojic s průmětem [-1/2;-1/2].
Nyní už lépe kontrastuje výsledek, který bychom dostali pro entanglované páry. Tam si sice musíme odpustit první měření, jelikož to by entanglement zničilo, nicméně v obou případech, v tom entanglovaném i neentanglovaném, víme, že součet průmětu spinů obou částic je nula, tj. že spiny obou částic jsou navzájem opačné. V tom neentanglovaném případě NAVÍC dokonce víme s jistotou, o jaký směr se jedná - proto bychom tedy mohli očekávat, že rozptyl výsledků pro neentanglované dvojice bude menší než pro entanglované, protože u těch neentanglovaných známe stav částic detailněji. Jenže dopadne to právě naopak – měřením průmětu spinu v severojižním směru dostaneme pro 10000 entanglovaných dvojic pouze dvě skupiny výsledků: cca 5000 dvojic dopadne s výsledkem [+1/2;-1/2], zatímco zbylých cca 5000 dvojic s výsledem [-1/2;+1/2]. Ani pro jednu dvojici nedostaneme [+1/2;+1/2] nebo [-1/2;-1/2]. Právě toto je zásadní rozdíl oproti předchozímu výsledku získanému na neentanglovaných dvojicích.
Takže nyní už vidíme ten klíčový rozdíl. Mimochodem, často se píše, že z pohledu kvantové mechaniky částice v entanglované dvojici NEMÁ předem daný směr spinu. Všimněme si, že není problém připravit dvojici částic tak, aby každá z nich MĚLA předem daný směr spinu, získaná dvojice částic ale není entanglovaná dvojice, a paradoxy jako je EPR paradox pro ni nevznikají.
Matematicky se dá rozdíl mezi entanglovanou a neentanglovanou dvojicí popsat tak, že ta entanglovaná je superpozicí dvou rozdílných dvoučásticových stavů, kdežto ta neentanglovaná není takovou superpozicí. Neentanglovaná dvojice částic se spiny orientovanými ve „východozápadním“ směru se dá popsat buďto jako stav:
|+1/2 vz > |-1/2 vz>
(kde |+1/2 vz > znamená průmět spinu první částice +1/2 ve východozápadním směru, podobně pro druhou částici)
anebo jako stav:
|-1/2 vz > |+1/2 vz>
Oproti tomu entanglovaná dvojice je následující superpozicí:
|+1/2 vz > |-1/2 vz> + |-1/2 vz > |+1/2 vz>
Pravou podstatou entanglementu tedy není to, že v entanglované dvojici mají částice opačné spiny; nulovost součtu spinů je ve skutečnosti jen důsledkem jednoho konkrétního způsobu přípravy entanglované dvojice (lze získat i jiným způsobem entanglovanou dvojici částic, která nemá součet spinů nulový). Pravou podstatou entanglementu je ve skutečnosti právě zmíněná superpozice dvou různých dvoučásticových stavů. Právě tato superpozice vede k výsledkům tak rozdílným od výsledkům na neentaglovaných dvojicích.
Re: Re: Re: Re:
Richard Palkovac,2015-11-12 08:07:09
Dakujem Vam za obsiahlu odpoved na moju otazku, napriek tomu som ale nenasiel, alebo mozno nepostrehol odpoved na to co som sa pytal.
Mne je jasne ze entaglovana dvojica nemusi mat opacny spin. Dolezite je to prepojenie, teda ze nejaka vlastnost jednej castice je pevne prepojena s vlastnostou druhej castice.
Moja otazka teda znela :
Existuju vobec dokazy o tom, ze spin (alebo ina entaglovana vlastnost castic) sa po vzniku previazanych (entaglovanych) castic (pokym nenastane prve meranie) meni ?
Alebo je prave toto to einsteinovske chapanie ?
Re: Re: Re: Re: Re:
Pavel Brož,2015-11-12 22:23:10
Spin částic v entanglovaném páru (pokud se tedy jedná právě o případ entanglementu zmíněného v článku, tedy entanglementu spinových stupňů volnosti) je podle kvantové teorie naprosto neurčitý, a to nikoliv ve smyslu, že nějaký je a my ho jen neznáme, ale ve smyslu matematické identity, která platí pro entanglované páry, ale neplatí pro neentanglované páry. Abych to vysvětlil, budu nucen opět použít něco málo z kvantově mechanické symboliky. Neentanglovaný pár, kdy první částice má průmět spinu ve východozápadním směru +1/2, a druhá -1/2, je popsán stavovým vektorem:
|-1/2 vz> |+1/2 vz>
Tento vektor je odlišný od analogického vektoru popisujícího neentaglovaný pár orientovaný např. v severojižním směru:
|-1/2 sj> |+1/2 sj>
anebo neentanglovaný pár orientovaný např. ve směru „horno-dolním“:
|-1/2 hd> |+1/2 hd>
Zkrátka a dobře:
|-1/2 vz> |+1/2 vz> # |-1/2 sj> |+1/2 sj> # |-1/2 hd> |+1/2 hd>
Entanglovaný pár je ale popsán následujícím vektorem:
|+1/2 vz> |-1/2 vz> - |-1/2 vz> |+1/2 vz>
(pozn. – v minulém příspěvku jsem omylem napsal |+1/2 vz> |-1/2 vz> + |-1/2 vz> |+1/2 vz>, omlouvám se, pro entanglement dvou fermionů tam musí být minus)
o kterém se dá ukázat, že je identický s vektorem:
|+1/2 sj> |-1/2 sj> - |-1/2 sj> |+1/2 sj>
a dokonce je identický s jakýmkoliv vektorem:
|+1/2 ab> |-1/2 ab> - |-1/2 ab> |+1/2 ab>
kde ab je libovolně zvolený směr.
Naznačím důkaz tohoto tvrzení pro ekvivalenci vektoru pro entanglovaný pár vyjádřeného pomocí východozápadního směru s vektorem vyjádřeným pomocí severojižního směru. Budeme muset bohužel skousnout následující vztahy, které vyjadřují vztah mezi vektory popisujícími spiny v různých směrech:
|+1/2 vz> = (1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj>
|-1/2 vz> = -(1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj>
Nyní už stačí jenom dosazovat z těchto dvou vztahů a provést formální roznásobení:
|+1/2 vz> |-1/2 vz> - |-1/2 vz> |+1/2 vz> =
[(1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj> ][-(1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj>] -
[-(1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj> ][ (1/odm(2))|+1/2 sj> +(1/odm(2))|-1/2 sj>]
=
-(1/2)|+1/2 sj>|+1/2 sj> +(1/2)|+1/2 sj>|-1/2 sj>
-(1/2)|-1/2 sj>|+1/2 sj> +(1/2)|-1/2 sj>|-1/2 sj>
+(1/2)|+1/2 sj>|+1/2 sj> +(1/2)|+1/2 sj>|-1/2 sj>
-(1/2)|-1/2 sj>|+1/2 sj> -(1/2)|-1/2 sj>|-1/2 sj>
= |+1/2 sj>|-1/2 sj> -|-1/2 sj>|+1/2 sj>
Takže vidíme, že je to opravdu identita (tato identita lze dokázat obecně pro libovolné dva směry, které nemusí být na sebe kolmé, pouze ve vztazích mezi vektory spinů v různých směrech budou místo koeficientů 1/odm(2) či -1/odm(2) figurovat siny a cosiny úhlů mezi osami).
Můžeme si to představit tak, že neentanglovaný a maximálně entanglovaný pár jsou dva extrémní případy částečného entanglementu, který můžeme popsat jakýmsi směrovým elipsoidem. Neentanglovaný pár pak bude odpovídat případu, kdy tento elipsoid degeneruje do úsečky v nějakém konkrétním směru (tj. případu, kdy dvě z os elipsoidu jsou nulové), zatímco maximálně entanglovaný pár bude odpovídat elipsoidu se stejně dlouhými poloosami, tedy kulové ploše.
U maximálního entanglementu tedy nelze určit žádný význačný směr, a to nikoliv proto, že bychom ho neznali, ale proto, že maximální entanglement žádný směr nemá, stejně jako jej nemá kulová plocha. Proto taky v kvantové teorii nelze hovořit o tom, jestli si spin entanglovaných částic drží před prvním měřením svůj směr či nikoliv, protože tato otázka tam nedává smysl, bylo by to opět jako se ptát, jestli si kulová plocha drží či nedrží směr. Pokud se ale bavíme pouze o částečném entanglementu, kde jistý význačný směr definovat lze, tak tam lze ukázat, že ten směr se drží úplně stejně, jako u neentanglovaných částic.
Re: Re: Re: Re: Re: Re:
Richard Palkovac,2015-11-13 07:37:03
Dakujem Vam opat za obsiahlu odpoved.
S Vasim tvrdenim :
"Spin částic v entanglovaném páru (pokud se tedy jedná právě o případ entanglementu zmíněného v článku, tedy entanglementu spinových stupňů volnosti) je podle kvantové teorie naprosto neurčitý, a to nikoliv ve smyslu, že nějaký je a my ho jen neznáme, ale ve smyslu matematické identity"
absolutne suhlasim a je mi to uplne jasne. Ja som ale svoju povodnu otazku polozil nie s pohladu kvantovej teorie ale z pohladu obecneho.
Spytam sa ale este inac, na Vas nazor. Pripustate taku moznost, (rozmyslal ste niekedy nad tym) ze kvantova neurcitost je sposobena nenulovou velkostou Planckovho casu ? Teda, ze existuje minimalny fyzicky mozny casovy interval , ktory nemoze byt nulovy a preto je stav castic presne nemeratelny a teda je neurcity ?
Re: Re: Re: Re: Re: Re: Re:
Pavel Brož,2015-11-13 10:05:16
Pokud se ještě vrátím k té Vaší předchozí otázce, tak na ni nelze odpovědět jinak, než z pohledu teorie. Pokud totiž máme entanglovaný pár, tak chování spinu částic v něm můžeme zjistit jenom měřením. Jenže otázka zněla jak se chová spin před tím měřením. Na to tedy v principu nemůže přinést odpověď experiment, teorie ale ano. Teď se jedná jen o to, jakou teorii upřednostníme. Podle kvantové teorie má částice v entanglovaném páru před měřením "všechny směry spinů zároveň", což se také opisuje tvrzením, že podle kvantové teorie částice v entanglovaném páru nemá před měřením žádný konkrétní směr, o kterém bychom pouze nevěděli. Podle teorií se skrytými parametry částice v entanglovaném páru před prvním měřením naopak má nějaký konkrétní směr, pouze o něm nevíme.
Co se týče Vaší otázky ohledně vztahu nenulovosti Planckova času a kvantové neurčitosti, tak samozřejmě zkonstruovat jakoukoliv hypotézu dávající do spojitosti cokoliv je kdykoliv možné, otázkou je, jakou má pak reálnou předpovědní sílu. Nad podobnými souvztažnostmi jsem taky nejednou přemýšlel, ale nakonec jsem je zavrhnul, zmíním zde jen pár důvodů proč. Jednak Planckova délka a čas jsou dodnes jen hypotetické veličiny, pro něž neexistuje jediný experimentální náznak, plynou jenom z jedné široké (a mainstreamové) kategorie teorií, které mají sloučit kvantovou teorii a gravitaci. Planckovou délku i čas získáme tak, že konstruujeme veličiny s odpovídajícím rozměrem délky či času ze základních konstant, kdy za jednu bereme Planckovu konstantu, za druhou rychlost světla, za třetí gravitační konstantu. Pokud bychom vzali místo těchto tří jinou trojici konstant - tak třeba Planckovu konstantu, rychlost světla a velikost elementárního náboje - tak dostaneme řádově úplně jiné hodnoty. Např. pro délku nám vyjde místo cca 10^-35 m veličina o dvacet řádů větší. Také bychom mohli vzít třeba Planckovu konstantu, rychlost světla a hmotnost elektronu jako nejlehčí nabité částice. Pak nám jako délka vyjde zase něco jiného, konkrétně Comptonova vlnová délka elektronu.
Je to pouze víra, že zrovna ty tři konstanty, Planckova konstanta, rychlost světla a gravitační konstanta, musí hrát fundamentální roli pro popis všech veličin, včetně délky a času. Nikde není psáno, že tato víra musí být oprávněná.
Kvantové jevy byly objeveny v jevech nezávislých na gravitaci. Gravitační síla působící na elektron v atomu je o čtyřicet řádů slabší, než síla elektrická, nehraje tam tedy žádnou roli. Totéž platí pro interferenční jevy, a vlastně pro všechny známé jak mikro- tak makroskopické kvantové jevy, těmi posledními jsou třeba supratekutost a supravodivost. Ve všech těchto jevech se kvantová neurčitost projevuje na až o více než třicet řádů větších vzdálenostech, než je Planckova délka, a při procesech trvajících až o více než čtyřicet řádů déle, než je Planckův čas. Bylo by tedy hodně troufalé očekávat, že všechny tyto jevy jsou projevem Planckovy délky nebo času.
To nejpodstatnější je ale to, že zatímco Planckův čas i délka jsou pouze spekulativní konstrukty, a teorie s nimi operující mají dodnes nulovou experimentální podporu, tak kvantová teorie naopak má neuvěřitelně obrovskou podporu v experimentálních datech díky obrovskému množství úspěšných kvalitativních i kvantitativních předpovědí, o kterých si teorie kvantové gravitace mohou pouze nechat zdát. Kvantová teorie přitom pro své předpovědi Planckův čas ani délku pro vysvětlení kvantové neurčitosti nepotřebuje, vůbec tyto veličiny neobsahuje. Naopak kvantové teorie gravitace se bez kvantové teorie neobejdou, všechny do jedné jsou pouze odvážnými rozšířeními kvantové teorie na popis gravitačních jevů.
strašidelné působení na dálku
Radim Šmíd,2015-11-05 23:01:03
Velice pěkný článek. Děkuji za něj.
Nějak ale nechápu "působení na dálku". Pokud je projevem tohoto působení 100% antikorelace měření stejné složky spinu na obou provázaných částicích, která se dá vyčíst z pozdějšího srovnání výsledků, tak ta přece může vzniknout už mechanizmem vzniku samotného entanglovaného páru.
Nenese si informaci o spinu částice sebou už od okamžiku vzniku páru?
Nějak se totiž spin musí rozhodnout do které hodnoty se překlopí v okamžiku interakce/měření.
Re: strašidelné působení na dálku
Pavel Brož,2015-11-05 23:10:37
Ano, samozřejmě dopředu nelze vyloučit, že spin se nějak deterministicky rozhoduje, kam se překlopí, a nám to pouze připadá náhodné. To, kam se překlopí, by pak mohlo záviset na nějakých nepozorovaných detailech, na nějakém skrytém parametru. Ale nemělo by záviset na tom, jak zrovna natočí osy vzdálený pozorovatel, který je kauzálně oddělen od prvého pozorovatele. Kouzlo Bellova důkazu je v tom, že se jedná o matematickou identitu odvozenou pouze na předpokladu, že měření na jednom místě sice může být ovlivněno jak nastavením místního přístroje, a třeba i nějakým skrytým parametrem, nemělo by ale záviset na tom, jak se zrovna rozhodne nastavit svůj přístroj vzdálený pozorovatel. Více jsem to rozepsal v odpovědi panu Hrnčiříkovi níže.
Re: strašidelné působení na dálku
Radim Šmíd,2015-11-05 23:29:49
Aha, takže kouzlo je v tom že směr mnou zvolené osy z je vzhledem k elektronu v podstatě náhodný? To mi ale spíš zní jako dálkové působení na měřící přístroj než na měřený objekt :)
Re: Re: strašidelné působení na dálku
Josef Hrncirik,2015-11-10 13:02:01
Chápu to tak, že naměřené porušení Bellovy nerovnosti značí že byly porušeny podmínky jejich platnosti, tj. reálně nastavení B působí na měření v A a naopak. Určitě tedy neplatí lokalita a objevuje se nadsvětelná či nekonečná rychlost vlivu vzdáleného nastavení.
Doufám, že to platí, pouze pokud na cestě k A i B je současně pouze 1 entanglovaný pár.
Při více párech by se asi mohla faktická informace šířit nadsvětelně.
I tak je to dostatečně strašidelné.
Re: Re: Re: strašidelné působení na dálku
Pavel Brož,2015-11-10 20:07:47
Ano, je to přesně tak. Naměřené porušení Bellových nerovností znamená, že byly porušeny podmínky, pro něž byly odvozeny.
Těmi podmínkami je nezávislost měření na jednom místě na nastavení na druhém místě. Bellovy ani CHSH nerovnosti ale neobsahují žádnou rychlost, která v nich figuruje. Tu rychlost tam dosazujeme my na základě limitů získaných z našich měření a porovnáváme ji s limitem plynoucích z jiných našich teorií - konkrétně ze speciální teorie relativity. Samotná skutečnost, že pozorování na jednom místě může záviset na vzdáleném nastavení není nijak záhadná, pokud se informace může od jednoho přístroje ke druhému přenést. Záhadné to začíná být až v okamžiku, když se obě měření stihnou provést v menším časovém rozdílu, než by to si stihla popovídat rychlostí světla, což je ten náš limit.
Svým způsobem tedy není ani tak problém v kvantové mechanice, protože ta se o maximální rychlost nestará, a okamžité působení v ní nepředstavuje problém. Problém je ve speciální teorii relativity. Podobná situace je v klasické Newtonově teorii gravitace, ta se taky o žádnou limitní rychlost nestará, a působení se v ní děje okamžitě, na dálku. Jenže my dnes díky mnoha experimentům bezpečně víme, že Newtonova teorie gravitace není přesná, a že ji správně (v rámci přesností měření) nahrazuje obecná teorie relativity, a ta limitní rychlost obsahuje - je jí rychlost světla. Podobně, jako jsme Newtonovu teorii gravitace nahradili obecnou teorií relativity, tak jsme i původní nerelativistickou kvantovou mechaniku chtěli nahradit relativistickou kvantovou mechanikou. Jenže ouvej, ono to není tak jednoduché, jako v případě Newtonovy gravitace. Ukazuje se, že sice existuje relativistické zobecnění původní nerelativistické kvantové mechaniky, ale že toto zobecnění je mnohem komplikovanější. Jednak si vynutí rozšíření z kvantové mechaniky, což je teorie popisující konstantní počet částic, na kvantovou teorii pole, což je teorie popisující proměnný počet částic, tj. popisuje i vznik, zánik, rozpad či přeměnu částic. To samo o sobě zní extrémně slibně, a opravdu to taky přináší úžasné výsledky - dnešní standardní model je dnes právě takovouto kvantovou teorií pole, a je to nejpřesnější teorie co se týče shody s experimentálními daty. Na druhou stranu se ale také ukazuje, že ono rozšíření původní kvantové mechaniky na relativistickou kvantovou teorii pole stejně neumožní eliminovat takové fenomény, jako je okamžitý kolaps vlnové funkce, a podobné axiomy. Prostě kvantová teorie pole je relativistickou teorií, která ale stejně to strašidelné působení na dálku obsahuje.
Na druhou stranu se dá ale obecně dokázat, že náhodnost, která chrání speciální relativitu před její diskvalifikací nelokálními korelacemi, zcela obecně zabraňuje při jakémkoliv měření získat informaci rychleji, než rychlostí světla. Není to tedy jenom o entanglovaných párech, ani při použití jejich libovolného počtu, dá se to dokázat naprosto obecně. Prostě pro jakékoliv sady měření jakýchkoliv veličin, a prováděných na jakémkoliv stavu systému, vychází, že ony nepochopitelné nelokální korelace se sice získají, ale informace se jimi nepřenese. Informace o těch korelacích se získá vždy až maximálně světelnou rychlostí. Prostě jako by se ta kvantová teorie s tou teorií relativity "spikly", že ta první tu druhou podrží.
Re: Re: Re: Re: strašidelné působení na dálku
Josef Hrncirik,2015-11-11 07:35:21
Mám jen podružné dotazy.
Pokud entanglované fotony jdou optickým vláknem a "odráží se od stěny vlákna, aby z vlákna nevystoupily, proč se neporušuje alespoň časem či mírně entanglement?
K určení korelací potřebuji proměřit mnoho entanglovaných fotonů dopadajících do A i B.
Existuje nějaký přímý důvod z KM, že je např. nutno mít na cestě mezi A a B v jedné vláknové cestě současně pouze 1 pár entanglovaných fotonů, ev. i jen 1 vláknovou cestu?
Nebo jinak. Lze vypustit smečku párů pouze postupně, nikoliv naráz či prakticky naráz do jediné či více cest a tím neumožnit i rychlé vyhodnocení statistiky korelace?
Není mi jasný vztah spinu fotonu a chování při průchodu polarizačním filtrem ev. polarizačním hranolem.
Zda filtrem foton buď projde nebo ne, a s jakou statistikou.
Jak souvisí třídění fotonů na řádné? a extraordinální? po průchodu pol. hranolem na ůhlu natočení hranolu a spinu? fotonu?
Lze získat (vyrobit) foton daného spinu, nebo jsou náhodné a musí se přetřídit?
Je toho příliš mnoho, něco bych si měl najít sám, ale ať vidíte co vrtá hlavou nepoučeným nespecialistům.
Třeba někdy do příště.
jednoduchy dotaz
Jirka Pospisil,2015-11-05 18:53:29
polozim primitivni otazku, ale jako lajk jsem zmaten.
pokud dobre chapu, entaglement plati do prvniho mereni. to je ale prilis antropocentricky pojem, castice neni "zmerena" prirodou hned pri jejich prvnich interakcich s okolnim svetem? jaka je vlastne definice pozorovatele a vubec, co je to mereni? nebo je mozne ze na spin se do te doby nikdo krome clovekem delegovaneho pristroje nepodival? diky za odpoved :-)
Re: jednoduchy dotaz
Pavel Brož,2015-11-05 23:17:16
Máte pravdu v tom, že tam vůbec nejde o to, zda to měření provádí člověk nebo příroda (i když někteří klasici kvantové teorie by se mnou právě v tomto zásadně nesouhlasili). Entanglement zaniká kolapsem společné vlnové funkce. My dodnes nevíme, co přesně tento kolaps vyvolává a jak přesně probíhá, my pouze víme, že dostatečně makroskopické systémy nemohou být ve stavech kvantových superpozic, které jsou naopak tak typické pro kvantové projevy mikrosvěta, a proto u nich předpokládáme, že kolaps jejich vlnové funkce musel proběhnout, a to i bez lidského přispění. My prostě nepozorujeme žádné Schrödingerovy napůl živé a napůl mrtvé kočky. Ani v tomto tvrzení ale se mnou nebudou všichni klasici kvantové teorie souhlasit, někteří totiž tvrdí, že k žádnému kolaspu vlnové funkce nedochází, ale že se štěpí celé vesmíry :-)
Hmmmmmm
Jaroslav Řezník,2015-11-04 11:40:58
Je to v každém případě fascinující a kontraintuitivní. Přesto se tam objevuje role vědomí. Co když je vědomí fyzikální úkaz? Nemám na mysli myšlení, představy, názory, paměť osobní ego, atd ale co když je to jakási fyzikální substance. Mění se myšlení, vědomosti, inteligence ale vědomí, identita jaksi zůstává stejné. Pamatuji si SEBE i jako dítě, nezemřel jsem po výměně buněk. Zajímavé jsou paradoxy. Budu skutečně identický sám se sebou, když se zkopíruji či přehraji do počítače? Tzv. koncept nesmrtelnosti, že sebe jaksi někam nahrajeme. Zcela jednoduše - myšlenkový experiment. někdo mě zkopríjuje ve tsejném čase - kde zůstane moje identita - u originálu či u kopie. nemůže být přeci v obou nebo v x dalších kopiích. připadá mi, že jaksi vědomí nelze dělit a že eje svým způsobem nečasové. Klidně přijmu jako základ světa jakési bezprostorové, bezčasé fyzikální vědomí. Myšlení, emoce, vlastní ego...to může vzniknout ale není to samo vědomí, je to jakýsi dodetečný obsah. Identita všech lidí se zdá jaksi stejná.
Zajímavé je, že zrovna kvantová fyzika na problém vědomí naráží. A biologie také neví co je to vědomí - ví o poškození myšlení, emocí, atd.......ale vědomí jako základ identity jaksi mimo myšlenkový, psychologický čas....vždy jsem to byl já, když si vzpmenu jak jsem jako 4 leté dítě bez vědomostí a vyspělého myšlení běžel třeba babičce naproti. Biologie také doufá jako kvantoví fyzici že se problém s vědomím nějak vyřeší. A že jaksi stroje naskočí do kontinulního vědomí, identifikace.
Re: Hmmmmmm
Richard Palkovac,2015-11-04 13:44:28
Na 100% si mozete byt isty jedinou existujucou "vecou" a tou je Vase vedomie. Svet ktory nim okolo seba vnimate moze byt objektivne existujuca realita , ale rovnako dobre to moze byt len iluzia.
Ked je vedomie len produktom mozgu (ciste materialisticky pohlad) tak ak by sa Vas podarilo dokonale skopirovat (v jednom momente) tak vzniknuta kopia by ste bol pre vsetkych ostatnych ludi "VY", ale pre Vas by to bol dalsi clovek, takze pre Vas to kopirovanie nedava zmysel.
Take kopirovanie, ale podla teorie mozne nie je (nie je mozne zistit vsetky vlastnosti castice naraz pre dokonale skopirovanie), je Vas mozne len teleportovat a to znamena, ze po teleportacii by ste Vy zomrel a Vasa "kopia" by si uvedomovala seba a myslela by si , ze ona je ten original. Pre Vas by to uz ale nemalo ziadny vyznam, vy by ste bol mrtvy. Pre Vasich blizkych by ste to ale bol stale Vy.
Ale ked vedomie nie je len produktom mozgu, ale produktom nejakej kvantovej previazanosti castic tela a castic vesmiru (taka hypoteza existuje ja som to nevymyslel) tak by mohlo byt vsetko inac :)
Este taka zaujimavost, ktora ma uz napadla davno. Pokial by existovala moznost skopirovat/teleportovat cloveka, tak od momentu ako sa o danej moznosti dozviete, si uz nemozete byt isty, ci ste "original".
Re: Hmmmmmm
Pavel Brož,2015-11-04 20:07:31
Souhlasím s tím, že vědomí bezesporu dosud je velkou a zároveň fascinující záhadou. Pouze nevěřím tomu, že s touto záhadou pomůže třeba zrovna kvantová teorie. Například ale Roger Penrose (https://cs.wikipedia.org/wiki/Roger_Penrose) si myslí opak, úžasná je jeho kniha Makrosvět, mikrosvět a lidská mysl, která vyšla i v češtině. Problémem vědomí se zabývalo hodně chytrých hlav z různých oborů lidského poznání, ať už to byli renomovaní odborníci z biologie, fyziologie, fyziky, neuronových sítí, atd. atd.. Nepochybuji o tom, že tato záhada ještě hodně pátků záhadou zůstane. A možná je tomu tak i dobře, třeba až si budeme umět vědomí naprosto logicky a racionálně vysvětlit, tak třeba pak budeme o něco chudší.
Re: Re: Hmmmmmm
Richard Palkovac,2015-11-05 09:40:12
O podstate vedomia rozmyslam uz minimalne 20 rokov. Dospel som sice k urcitym indiciam aj ciste z pohladu materialistickej vedy, ale urcite nie k rieseniam. V poslednom case sa uz ale skor priklanam k tomu, ze vedomie nie je mozne vysvetlit ciste materialisticky. Zaroven davam minimalne 50% sancu tomu, ze vedomie je jedina objektivne existujuca "vec" a vsetko ostatne je len iluzia.
To mi ale vobec nebrani studovat spravanie sa tej iluzie pomocou materialistickej vedy. Tu iluziu totiz stvoritel vytvoril tak, aby posobila presvedcivo materialistickym dojmom , asi mal nejaky nam zatial neznami zamer.
Otazka ohladom prenosu informacie
Richard Palkovac,2015-11-04 08:28:28
Dobry den.
Mozno som nieco nepochopil spravne, a moja otazka znie nasledovne :
Pozorovatel A a B sa dohodnu, ze budu merat spin toho isteho elektronu/pozitronu stale v osi "z". Potom sa ale pozorovatel A nahodne rozhodne, ze zacne robit meranie svojho elektronu v osi "x". Pozorovatel B ten okamih zisti, pretoze mu od toho okamihu v osi "z" zacnu vychadzat nahodne hodnoty spinu jeho pozitronu.
Nie je to prenos informacie ?
Re: Otazka ohladom prenosu informacie
Martin Ondracek,2015-11-04 09:40:24
Byl by to přenos informace, kdyby to bylo jak píšete. Ale pozorovatel B nezjistí ve skutečnosti vůbec nic, protože náhodné výsledky v ose z dostával i předtím, než pozorovatel A svou měřící osu změnil. Jen předtím ty výsledky pozorovatele B byly (anti)korelované s výsledky pozorovatele A, ale to pozorovatel B ve chvíli, kdy naměřil svůj výsledek, stejně neměl jak ověřit.
Re: Otazka ohladom prenosu informacie
Pavel Brož,2015-11-04 09:45:32
Ano, je to jak už napsal pan Ondráček. Pozorovateli B sice začnou vycházet náhodné hodnoty jeho spinu okamžitě, když A změní osu na jinou, on to ale zjistí až když oba pozorovatelé své výsledky porovnají, do té doby má v ruce náhodnou řadu dat, ze které samotné nemůže nic vyčíst. Právě tato náhodnost jednotlivých měření zachraňuje speciální teorii relativity tím, že zabraňuje přenosu informace nadsvětelnou rychlostí. Pozorovatel B sice má svá data okamžitě, ale informaci o antikorelacích či naopak nulových korelacích z nich vydoluje až po porovnání svých dat s daty pozorovatele A.
Re: Re: Otazka ohladom prenosu informacie
Richard Palkovac,2015-11-04 10:15:00
Dakujem Vam obom za odpoved.
Takze moja chyba v chapani bola nasledovna :
Myslel som si, ze ak zmeria pozorovatel A spin elektronu v osi "z", tak sa ten spin nastavi na zmeranu hodnotu a uz zostane tak, az pokym pozorvatel A neprevedie meranie v inej osi.
Pravda je ale taka, ze aj ked bude merat stale ten isty elektron a stale v tej istej osi, namerane hodnoty budu pri kazdom jednom merani nahodne.
Je to tak ?
Re: Re: Re: Otazka ohladom prenosu informacie
Martin Ondracek,2015-11-04 12:27:21
Není. Omlouvám se, při minulé odpovědi jsem nepozorně četl Váš předchozí příspěvek a představil jsem si sérii měření na různých elektronech/pozitronech, namísto měření na pořád jedné a té samé částici. Pokud bude pozorovatel měřit pořád ten samý pozitron a pořád v ose z, tak první výsledek bude náhodný a ty další stejné jako ten první. Pořád ale platí, že informace se mezi pozorovateli A a B žádným měřením na tom elektron-pozitronovém páru nedá přenést. Pozorovatel B bude pořád opakovaně měřit stejný výsledek i poté, co pozorovatel A libovolným působem změnil osu měření nebo cokoli jiného provedl se svým elektronem.
Re: Re: Re: Re: Otazka ohladom prenosu informacie
Richard Palkovac,2015-11-04 13:19:32
Dakujem za odpoved, ale nepozdava sa mi z nasledovneho dovodu :
Ak ma pozorovatel B uz zafixovany spin v ose "z" a je dohodnuty vopred s pozorvatelom A, ze on, pozorovatel B, nebude robit meranie v inej osi, to znamena, ze aj pozorovatel A uz ma zafixovany spin v ose "z".
Potom, ked pozorovatel A urobi meranie povedzme v osi "x" , uz bude mat na 100% presnu informaciu o spine v dvoch osiach.
Mozme mat 100% presnu informaciu o spine v dvoch osiach ?
Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Martin Ondracek,2015-11-04 15:26:27
Aktuální informaci o spinech ve dvou různých osách mít nemůžeme. Ve chvíli, kdy pozorovatel A provede měření na "svém" elektronu v ose x, tak si "rozhodí" (randomizuje) hodnotu spinu tohoto elektronu v ose z. Kdyby ještě následně měřil v ose z, tak dostane náhodný výsledek, nezávislý na tom, co naměřil pozorovatel B na svém pozitronu. Po provedení měření v ose x tedy pozorovatel A zná právě jen průmět spinu svého elektronu do osy x a až k němu dorazí zpráva o výsledcích pozorovatele B, bude navíc znát průmět spinu té druhé částice (pozitronu) do osy z. Jenže to už obě částice nejsou entanglované a spin pozitronu v ose z nic neříká o spinu elektronu v ose z. Pravda, mohl byste tvrdit, že v době od vzniku entanglovaného páru až do změření spinu elektronu v ose x měl tento elektron právě takový průmět spinu do osy x, jaký jste poté zjistil (pozorovatel A zjistil) svým měřením a zároveň právě takový průmět do osy z, jaký odpovídá výsledku měření pozorovatele B. Z tohoto pohledu by se to dalo brát jako znalost současných hodnot průmětů spinu jedné částice do dvou os. To je asi otázka inetrpretace. Mimochodem, analogicky by se dal zkonstruovat myšlenkový experiment s více než dvěma entanglovanými částicemi, kde by se takto zjišťoval průmět spinu do většího počtu různých os. Je to ale vždycky znalost o stavu v minulosti, kterou získáte, až když svým měřením tento stav zrušíte. A je dobrý důvod k tomu, proč se tato interpretace obvykle neuvažuje: Není zrovna praktická, protože ten hypotetický stav elektronu s jednoznačně definovanou hodnotou spinu ve různých dvou osách už se nikdy v budoucnu nijak neprojeví, relevantní je jen ten skutečně naměřený průmět do osy x.
Re: Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Richard Palkovac,2015-11-04 16:34:40
Je mozne , ze nechapem, kedy dojde k ukonceniu/preruseniu entaglovania elektronu a pozitronu. Doteraz som to chapal tak, ze nezalezi na pocte kolko merani urobi pozorovatel A alebo B , castice su stale entaglovane.
Popisem to podrobnejsie. Pozorovatel A aj B maju synchronizovane hodiny a presne v sekundovych intervaloch (ked nastane cela sekunda) robia merania nasledovne :
Pozorovatel B robi stale (ked nastane cela sekunda) len meranie spinu svojho pozitronu v osi "z". Po prvom merani posle spravu pozorovatelovi A o spine v osi "z". Kedze B robi aj nadalej stale meranie len v osi "z" uz dalsie spravy nemusi posielat lebo vieme ze nameria stale to iste (na tom sme sa uz zhodli).
Ked k pozorovatelovi A dorazi sprava, a nastane najblizsia "meracia (cela)" sekunda urobi meranie v osi "x". Meranie v osi "z" nepotrebuje robit, lebo vie co musel namerat B v tej istej sekunde (nepotrebuje k tomu dalsiu spravu od B). Takze A ma spin v dvoch osiach.
Jedine, ze doslo medzi tym niekedy k preruseniu entaglovania a vysvetlite mi ze kedy.
Re: Re: Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Martin Ondracek,2015-11-04 18:09:38
V tom vašem příkladě pozorovatel A zná průmět své částice do osy z (díky zprávě od B) těsně před tím, než provedl své vlastní měření (po zlomek sekundy od chvíle, kdz dorazí zpráva, až k nejbližší celé sekunkdě, kdy začne měřit), a zná průmět do osy x hned poté, co své měření provedl. To ale není současně. Po provedení měření, kdy zná průmět do x, už pozorovatel A průmět do osy z nezná, protože měřením průmětu do x se mohl průmět do z změnit. Můžete se ptát, jak je to přesně v okamžiku měření. Na přesnou odpověď by bylo třeba znát detaily mechanizmu toho měření a obecně je to složitá záležitost, ale v každém případě ta dříve známá hodnota v ose z se naruší díky interakci s měřícím přístrojem už v průběhu měření, které ve skutečnosti vždycky potrvá nějakou nenulovou (byť krátkou) dobu, zatímco výsledek o průmětu do osy x se pozorovatel A dozví až po skončení měření. Takže když bereme v úvahu tu dobu, kdy měření probíhá, tak vlastně v tomto okamžiku není dobře definována hodnota ani jednoho z obou průmětů, ani z, ani x.
Jinak k ukončení entanglementu ("kolapsu" entanglovaného stavu) dojde už při prvním měření. To může vypadat paradoxně, když se entanglement projevuje až při porovnání výsledků měření obou částic. Formální popis celého procesu vypadá tak, že když pozorovatel, který provádí měření jako první (v našem případě B) naměří dejme tomu průmět do osy z +1/2, tak elektron-pozitronový pár přejde do stavu, který se dá slovně popsat takto: "Pozitron má průmět spinu do osy z +1/2 a současně elekton má průmět spinu do osy z -1/2". Právě popsaný stav ale už není entanglovaným stavem, entanglovaný stav, který existoval před měřením, prostě jen zajistil, že ten nový stav vypadá, tak jak vypadá: spiny obou částic jsou opačné, ale teď už jen v průmětu do osy z. Kdyby namísto toho jako první měřil pozorovatel A a naměřil dejme tomu průmět do osy x +1/2, tak by nový stav páru po tomto prvním měření byl: "Pozitron má průmět do osy x -1/2 a elektron průmět do osy x +1/2." To opět už není entanglovaný stav. Spiny jsou zase opačné, ale tentokrát jen v ose x. Původně existující entanglovaný stav tedy garantuje, že ať už zvolíme měřící osu pro první měření jakoukoli, měřením dostaneme vždy stav, kdy částice mají vzájemně opačný spin definovaný v té zvolené ose. Uznávám, že to zní hrozně zamotaně, ale částečně je to tím, že kvantová fyzika opravdu není snadno pochopitelná, částečně pak tím, že se snažím převést do neformálního slovního popisu něco, co bych normálně vyjádřil matematickými pojmy typu "Hilbertův prostor", "superpozice", "projekce" apod. a zapisoval to Diracovým braketovým formalismem. Pro nezasvěcené by to byly nesrozumitelné šifry, ale pro toho, kdo ten formalizmus zná, by to bylo přehlednější.
Mimochodem, jestli znáte teorii relativity, tak by vám to, co jsem výše napsal o kolapsu entanglovaného stavu, mělo připadat podezřelé. Vypadá to, jako by průběh a výsledek experimentu závisel na tom, jestli jako první měří pozorovatel A, nebo pozorovatel B. Tak, jak jste to popsal ve svém příkladu, je jasné, že jako první měří B, pošle zprávu, pak teprve měří A. Kdyby se ale žádná zpráva neposílala a měření obou pozorovatelů proběhla téměř současně, s tak krátkým časovým odstupem, že by zpráva od žádného z nich k tomu druhému ani nemohla stihnout dorazit, tak by mělo být relativní, který z nich měří dříve a který později. Právě takové situace nastávala (záměrně) i v experimentu, o němž referuje článek, pod kterým diskutujeme. Řešení zdánlivého rozporu s relativitou je takové, že i když se formální popis toho, co se děje, bude poněkud lišit v závislosti na tom, zda za první měření prohlásíme měření pozorovatele A, nebo měření pozorovatele B, tak všechny skutečně naměřené (nebo i aspoň v principu měřitelné) výsledky budou stejné.
Re: Re: Re: Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Richard Palkovac,2015-11-04 20:44:44
Ak som spravne pochopil tento Vas posledny prispevok, tak sa mozeme vratit k mojej povodnej otazke, uplne na zaciatku tohoto vlakna. Teraz ked si ju precitate znovu, mozno odpoviete inac na nu ako predtym.
Je tiez mozne ze to jednoducho nie som schopny pochopit, v takom pripade Vas uz dalej nebudem trapit :)
navrat na zacatek
Martin Ondracek,2015-11-04 22:11:55
Ne, odpovím stejně, jako jsem odpověděl na druhý pokus (poté, co jsem si uvědomil, že se ptáte na opakované měření jednoho a toho samého páru částic). Pozorovatel B bude při opakovaném měření v ose z dostávat pořád jednu a tu samou hodnotu, bez ohledu na to, co s tou druhou částicí provádí pozorovatel A. Entaglement přežije jen do prvního měření a přímo ovlivní jen korelaci první dvojice měření: první měření pozorovatele B a první měření pozorovatele A. Samozřejmě, dokud budou oba pozorovatelé měřit jen v ose z, tak díky tomu, že budou dostávat pořád stejné výsledky, bude i jakákoli další dvojice spinů (anti)korelovaná, prostě proto, že bude stejná, jako ta první. To ale není tím, že by entaglement přetrvával. Jakmile pozorovatel A začne měřit v jiné ose, tak jeho výsledek nebude už někdejším entanglementem nijak ovlivněn. Pozorovatel B si ničeho nevšimne, měří pořád to samé, spiny obou částic v tuto chvíli spolu už nijak nesouvisí. Kdyby se pozorovatel A později vrátil k měření v ose z, dostane náhodný výsledek, tedy s 50% pravděpodobností stejný, jako při svém prvním měření v ose z (a tedy opačný, než pozorovatel B) a s 50% pravděpodobností opačný, než při svém prvním měření (a tedy stejný, jako pozorovatel B). Tuto novou hodnotu pak při případném dalším opakování měření v ose z bude reprodukovat, zase dokud svou osu nezmění. Pozorovatel B mezitím měří pořád tu samou hodnotu, co kdykoli předtím, protože on svou osu nikdy nezměnil a měří pořád v z. Takže poté, co se A vrátil k měření v ose z po měření v ose x a B stále jen opakuje měření v z bez přerušení, není mezi jejich výsledky už žádná vzájemná provázanost.
P.S.: Trápit mě klidně můžete dál, aspoň si pořádně srovnám v hlavě, jak to funguje a jak se to dá vysvětlit jným lidem.
Re: navrat na zacatek
Richard Palkovac,2015-11-05 05:19:06
Dakujem, takze Vas idem trapit dalej .
Pisete : " A začne měřit v jiné ose, tak jeho výsledek nebude už někdejším entanglementem nijak ovlivněn. Pozorovatel B si ničeho nevšimne, měří pořád to samé, spiny obou částic v tuto chvíli spolu už nijak nesouvisí. Kdyby se pozorovatel A později vrátil k měření v ose z, dostane náhodný výsledek, tedy s 50% pravděpodobností stejný, jako při svém prvním měření v ose z (a tedy opačný, než pozorovatel B)"
Z toho mi vyplyva, ze pre pozorovatela A plati ina realita ako pre pozorovatela B (alebo iny entaglement). Chapal by som to, ak by pozorovatel B neprevadzal stale meranie vo svojej osi "z". Ale on to stale robi a stale mu vychadza rovnaky spin. Ako teda mozne byt pravdive Vase tvrdenie :"Kdyby se pozorovatel A později vrátil k měření v ose z, dostane náhodný výsledek, tedy s 50% pravděpodobností stejný, jako při svém prvním měření v ose z (a tedy opačný, než pozorovatel B)" ?
Pozorovatel B predsa nema ziadnu moznost dostat v osi "z" nahodny vysledok , teda opacny ako nahodny vysledok pozorovatela A v osi "z".
Re: Re: navrat na zacatek
Martin Ondracek,2015-11-05 10:31:24
Realita určitě platí pro oba pozorovatele stejná. Problém může být v tom, co přesně je realita, třeba přesný okamžik zániku entanglovaného stavu může být relativní, jak jsem vysvětloval výše, protože je to spíš formalizmus, než něco reálně pozorovatelného. V každém případě jsou ale realitou naměřené výsledky, ty si konec konců mohou oba pozorovatelé později navzájem sdělit, takže i kdyby byla realita v principu subjektivní, tak se součástí reality jednoho pozorovatele mohou časem stát výsledky toho druhého. V naměřených výsledcích tedy nemůže být žádný rozpor ve smyslu, že by pozorovatel B něco naměřil a pozorovatel A přitom viděl, že B naměřil něco jiného. Jestli se z kteréhokoli mého předchozího příspěvku zdá, že takový paradox popisuji, tak jsem se špatně vyjádřil, nebo jste to špatně pochopil.
Teď se pokusím vyjasnit konkrétně to, na co se ptáte ve svém zatím posledním příspěvku, ale nejsem si jistý, jestli dobře chápu, v čem vidíte problém. Zkusím vyjít zejména z poslední věty toho Vašeho příspěvku. Kdybych odpovídal na něco jiného, něž na co se ptáte, zkuste ten dodaz rozvést podrobněji. Situace, o které se bavíme, je, jestli to dobře chápu, tato: Pozorovatel B stále opakuje své měření v ose z, pozorovatel A provádí první měření, kterým se vrací k měření v ose z poté, co předtím měřil (nějakou dobu nebo jen jednou, na tom nezáleží) v ose x. Pozorovatel B měří pořád to samé, na tom jsme se už shodli. V tomto smyslu jsou tedy jeho výsledky nenáhodné: Náhodný byl výsledek jeho prvního měření v řadě, ty ostatní už jsou stejné.
(Poznámka: Protože víme s jistotou, že výsledky opakovaných měření pozorovatele B musejí být stále stejné, tak je to jeho měření vlastně trochu zbytečné. Ale nebudu věci komplikovat tím, že bych uprostřed diskuze měnil pravidla myšlenkového experimentu, a tak nechám pozorovatele B do zhloupnutí měřit opakovaně to samé v souladu s původním zadáním na začátku vlákna.)
Ve chvíli, kdy se pozorovatel A vrací k měření v ose z, dostane náhodný výsledek nezávislý na výsledku měřeném pozorovatelem B. Jestli se tedy ve své poslední větě ptáte na tento náhodný výsledek pozorovatele A, tak ten může, ale nemusí, být opačný k výsledku pozorovatele B. Jestli se naopak ptáte na úplně první výsledek pozorovatele A v ose z, ještě před tím než pozorovatel A přešel do osy x, tak ten naopak nutně bude opačný než první výsledek pozorovatele B (i než všechny ostatní výsledky pozorovatele B, protože ty jsou stejné, jako ten první). Úplě první dvojice měření v ose z, tj. úplně první měření pozorovatele A a první měření pozorovatele B jsou tedy náhodné, ale s tou podmínkou, že jsou navzájem opačné. Takže se na tato dvě měření můžeme dívat tak, že jedno z nich má náhodný výsledek (lhostejno které) a výsledek toho druhého je tím prvním determinován.
Pro další pokračovaní diskuze bychom možná mohli založit nové vlákno, tohle se začíná stávat dost nepřehledným.
Re: Re: Re: navrat na zacatek
Richard Palkovac,2015-11-05 14:49:34
Myslim, ze uz to za chvilu ukoncime, takze netreba nove vlakno, pretoze z Vasho posledneho prispevkuu je mi jasne, ze chapete sposob merania aky popisujem.
Pisete : "Ve chvíli, kdy se pozorovatel A vrací k měření v ose z, dostane náhodný výsledek nezávislý na výsledku měřeném pozorovatelem B. Jestli se tedy ve své poslední větě ptáte na tento náhodný výsledek pozorovatele A, tak ten může, ale nemusí, být opačný k výsledku pozorovatele B."
Toto vase tvrdenie chapem a nemam snim ziadny problem (napisal ste to uz aj predtym tak isto spravne, ako pozeram, ale ja som to zle pochopil) a z toho mi vyplyva, ze castice uz nie su prepojene.
V podstate podla toho, su castice prepojene len pocas prveho merania a potom je po "zazraku", prepojenie sa prerusi.
Z povodneho clanku som mal dojem, ze prepojenie pretrvava aj nadalej a mozme merat do nekonecna bez zrusenia prepojenia, preto toto cele vzniklo.
zaver
Martin Ondracek,2015-11-05 16:01:23
Výborně, myslím, že je to vyřešeno. Mimochodem, v případě, o kterém jsme tady celou dobu diskutovali, není na entanglementu tajemné opravdu vůbec nic. Docela dobře by se dal vysvětlit nějakou (náhodnou, ale korelovanou) informací, kterou si částice s sebou nesou od svého vzniku. Šlo by tedy o teorii se skrytými parametry, teorii "realistickou" v tom smyslu, že stav částic by byl plně určen těmi sice "skrytými", ale reálně existujícími parametry, a dokonce "lokálně realistickou", protože ty parametry by se mohly nastavit jako korelované, už když částice společně vznikaly, a nemuselo by docházet k žádnému působení na dálku. Ty intuitivně celkem přijatelné (doufám) výsledky, nevzpírající se lokálně realistické interpretaci, jsme dostali díky tomu, že jsme se omezili na taková měření, kdy buď oba pozorovatelé měří ve stejné ose, nebo v osách navzájem komých. Potíže pro jakoukoli lokálně realistickou interpretaci nastanou až tehdy, když se začneme zabývat měřením v osách pootočených o nějaký obecný úhel (třeba 45°). V takových případech může podle kvantové teorie dojít k narušení Bellových nerovností (zmíněných v článku) které by pro každou lokálně realistickou teorii měly platit. Pak teprve je vlastně entanglement opravdu zajímavý. Ale i v tom případě platí, že entanglement se projeví jen zvláštní korelací prvního páru měření. Při případném dalším opakování měření se stejnými částicemi pak už dostáváme to, co bychom očekávali na základě výsledku prvního měření (v případě měření pořád ve stejné ose pořád totéž). Navíc nestačí změřit jeden pár, pro ten to v případě nerovnoběžných (např. o těch 45° otočených) os může výjít tak i onak, tj. oba pozorovatelé můžou naměřit stejnou nebo opačnou hodnotu. Zajímavé jsou až konkrétní pravděpodobnosti, které se dají ověřit jen mnohonásobným opakováním pokusu (vždy na nově generovaném páru částic, samozřejmě).
Re: zaver
Richard Palkovac,2015-11-05 16:22:28
Pokial by to slo vysvetlit "skrytymi" parametrami existujucimi pri vzniku castic, teda "einsteinovsky", tak by to nebol vobec zazrak, ale tusim, ze vsetky tieto pokusy chcu dokazat prave to, ze ziadne skryte parametre pri vzniku tam nie su a okamzite posobenie na dialku existuje, len sa nim nic materialne a ani ziadna informacia neda preniest.
Dakujem Vam za trpezlivost pri vysvetlovani.
monogamie
Martin Ondracek,2015-11-04 16:09:21
Beru zpět tvrzení z mého předchozího příspěvku o možném zobecnění experimentu na více než dvě částice. To jsem si zase něco představoval jak Hurvínek válku. Ve skutečnosti by tomu zobecnění bránila tzv. monogamie entaglementu, která znamená, že dvě maximálně entanglované částice nemohou být entanglované s ničím třetím.
Re: Re: Re: Re: Otazka ohladom prenosu informacie
Michal Lichvár,2015-11-04 13:39:38
A na tomto by nesiel postavit protokol na posielanie sprav?
3 citania po sebe rovnakej hodnoty su 0
3 citania po sebe roznych hodnot su 1
(rychlo strielam myslienku)
Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Martin Ondracek,2015-11-04 15:29:28
Nechápu, jak to myslíte. Hodnoty čeho přesně by se měly číst a jak by odesilatel zprávy zajistil, že budou podle potřeby buď stejné, nebo různé?
Re: Re: Re: Re: Re: Re: Otazka ohladom prenosu informacie
Michal Lichvár,2015-11-05 13:47:16
Ok, asi uz nic. Ja som doteraz v tom, ze entanglement, ci sparovanie castic je trvale, nie len do prveho merania. Moja otazka smerovalo k teleportacie informacie. Ak by bol entanglement trvaly pre dvojicu castic, jedna by mohla menit a na druhej zmena detekovat, cize prenos informacie by bol rychlejsi ako prenos svetla.
Priznávam sa
Rene Mikolas,2015-11-03 16:26:14
A to bez mučenia, že som blbý a ničomu nerozumiem. Súčasne sa šľahám ako príslušník Opus Dei a obidve vety nižšie uvedené sú, v zmysle kvantovej mechaniky, súčasne platné:
1. Som blbý a som na to hrdý.
2. Som blbý a nie som na to hrdý.
Len to mi nie je jasné ako som mohol na výške preliezť cez fyziku a to vďaka otázke na Heisenbergov princíp neurčitosti.
Jediné odpočinutie v lone Abraháma a spočinutie v náručí Pána, ako ateista , vidím v úplne inej téme.
Dnes ma osvietilo a vykúpenie mi poskytuje hypotéza, že čas pred singularitou plynul opačne. Teda singularita bola bodom obratu. Tak padla moja predošlá hypotéza o neexistencii hmoty, priestoru a času pred singularitou.
Znamená to, že svet energie pred singularitou bol aj svetom opačne plynúceho času.
A z toho mi vyplýva, že ani v Čiernych dierach sa nesnaží hmota zavrieť priestor, ale snaží sa aj zároveň prepólovať čas.
Táto nová hypotéza nenarúša moju predošlú hypotézu o dvojitom Big Bangu. A naopak poodhaľuje tajomný pôvod Tmavej hmoty a Tmavej energie ako svetov s opačne plynúcim časom v našom vesmíre. Vysvetľuje to, prečo sa pozorovatelia vo vesmíre s Tmavou hmotou a našom vesmíre nemôžu navzájom vidieť, ale nevylučuje to ich vzájomné pôsobenie, lebo gravitácia, sa na rozdiel od ostatných troch síl, nedá ničím odtieniť.
Re: Priznávam sa
Rene Mikolas,2015-11-03 16:42:20
A tu so práve teraz našiel niečo zo starých nálezov:
V článku “Průjezdné červí díry v multimetrické gravitaci” (OSEL) M.Hohmann predpokladá “Částice z odlišných kopií o sobě ale prakticky nevědí a působí na sebe jedině gravitací.” Tým sa zhoduje s tvrdením v mojej hypotéze Double Big Bangs.
Re: Priznávam sa
Michal Lichvár,2015-11-04 13:48:01
A ako sa vobec pozerat na plynutie casu? Co je cas, rozmer?
Re: Re: Priznávam sa
Rene Mikolas,2015-11-05 00:36:55
Ano napadlo ma to, keď sa pozerám na tie spiny z tohto článku a keď hovoria o priemetoch do všetkých troch osí.
Čas ako rozmer a súčasne kolmý na všetky tri súradnice nášho vesmíru a jeho šipka má len dva možné smery - navzájom protichodné.
Re: Re: Re: Priznávam sa
Michal Lichvár,2015-11-05 14:01:48
V tom pripade cas neplynie, ale my plynieme v casopriestore jednym smerom.
Predstavujem si to tak, ako keby sputany vazen bol prevazany vagonom po zeleznici , mal len uzke okno, ktorym by videl meniaci sa horizont. Po nalozeni do vlaku stratil pamat, jedine co pozna, je ten uzky pohlad.
Zprava by prichadzal novy horizont = buducnost; vlavo by horizont mizol = minulost.
2D pohlad v 3D svete. Vie ze existuje 3rozmer, ale nevie ovplyvnit smer ani rychlost.
Vela filozofickych otazok ta kvantovka vyvolava. Aby to nakoniec nebolo tak, ako je pisane vo vedach, alebo inych staroindickych textoch. Nekonecne vedomie, nirvana, reinkarnacia vedomia. Mozog ako struktura, ktora je v istom priereze casopriestorom hostit vedomie.
Pripadne vedomie by bolo podhubim, mozog plodnica/hrib. Podhubie je takmer 2D, funguje na povrchu nejakej plochy, plodnice je expanzia do tretieho priestoru.
Ok, spekulovania, filozofia.
synchronizace a spiny
Milan Krnic,2015-11-03 10:15:11
Jak přesná je synchronizace měření pozorovatelů? Ona zmiňované "každé měření provedou v přesně stejný okamžik" je přeci nesmysl. Přesnost je může "něčemu" nějak blížit..
S těm spinům. U spinu tedy měříme v určitém úhlu hodnotu energie? Jak?
Děkuji.
Re: Re: synchronizace a spiny
Rene Mikolas,2015-11-03 15:54:46
Tí pozorovatelia ma tiež napínali, ale už na to kašlem.
Re: Re: Re: synchronizace a spiny
Milan Krnic,2015-11-04 06:36:19
No, mě ani tak ty "přesné okamžiky synchronizace" nenapínají, jako znechucují, protože to je jasný nesmysl.
U spinů mi je pak pravděpodobně jasné, jak "hraje" ve spintronice - elektrony NATÁČEJÍ spiny podle směru magnetizace, a Hallův jev nám umožňuje tyto spiny měřit prostřednictvím příčného elektrického napětí - to je jednoduché.
Ale jak je to realizováno v těchto experimentech s měřením úhlu a energie spínu, to mi zůstává záhadou.
Re: Re: Re: Re: synchronizace a spiny
Pavel Brož,2015-11-04 09:40:31
Ten termín "přesný okamžik" je samozřejmě zkratka za větu např. "provádějí měření v pokud možno stejném čase, každopádně ale tak, aby rozdíl v časech jejich měření byl výrazně menší, než by byla doba, za kterou by mezi nimi mohl přeletět světelnou rychlostí nějaký signál, který by mohl vzdálený výsledek ovlivnit". Zajisté uznáte, že psát všude tu druhou možnost je neúnosné. Myšleno to bylo ale právě takto.
Jinak ve spintronice se spiny opravdu natáčejí magnetickým polem jak píšete, ale nejenom ve spintronice, platí to také pro nespárované elektrony v atomech, anebo i pro atomová jádra v krystalických mřížích. Tam se elektron nebo jádro může natočit hned dvěma navzájem opačnými způsoby, buď po směru či proti směru vnějšího pole. Jeden z nich má ale menší energii než ten druhý, proto ten s vyšší energií může v krátké době přeskočit do energeticky výhodnějšího stavu, takže ve výsledku budete mít shodně orientované spiny elektronů či jader, podle toho co měříte.
Re: Re: Re: Re: Re: synchronizace a spiny
Milan Krnic,2015-11-05 07:46:56
Jakým způsobem ale měříme energii spinu, viz článek "B měří v osách o 45 stupňů pootočených vůči osám pozorovatele A"? To nechápu.
Re: Re: Re: Re: Re: Re: synchronizace a spiny
Pavel Brož,2015-11-05 23:23:22
Energie není vlastnost spinu samotného, energii může mít až částice. Dá se přitom ukázat, že u elektricky nabité částice vázané v nějakém systému, pokud tato má spin (tedy např. u elektronu), závisí její energie na směru spinu, pokud se ten systém nalézá ve vnějším magnetickém poli. To se projevuje např. rozštěpením spektrálních čar atomů, pokud tyto atomy umístíme do vnějšího magnetického pole, kdy se čáry rozštěpí na dvojice čar, kdy jedna odpovídá těm atomům, ve kterých se příslušný elektron zorientoval ve směru magnetického pole, kdežto druhá z té dvojice čar odpovídá těm atomům, kde se elektron zorientoval proti směru magnetického pole.
Re: Re: Re: Re: Re: Re: Re: synchronizace a spiny
Milan Krnic,2015-11-06 06:39:44
To chápu. Ovšem v článku uvádíte. že "pozorovatel B měří v osách o 45 stupňů pootočených vůči osám pozorovatele A".
A nejde mi do hlavy, když spin částice otočíme do určitého směru pomocí energie, např. magnetického pole. Co znamená, že druhý pozorovatel měří v osách o 45 stupňů pootočených.
To mají oba "identické systémy" - magnetické pole stejné energie, ale jeden ho má pootočené o těch 45 stupňů?
kvantová dogmata
Petr Petr,2015-11-03 08:50:26
Stejně jako v článku pana Mihulky se ptám jak to je s tímto rozporem:
Klasicky jde dosáhnout 2,54 (experimentálně bylo dosaženo až 2,679) a tedy více než proklamovaná 2.
http://arxiv.org/pdf/1506.01305v2.pdf
http://phys.org/news/2015-07-line-quantum-classical-world.html
jděte už někam s těma školskejma pravdama...
(aneb stokrát opakovaná lež se stane pravdou)
Re: kvantová dogmata
Milan Krnic,2015-11-03 09:53:47
Součet velikostí vnitřních úhlů trojúhelníku také není roven 180°, jak nám pravila paní učitelka.
Takových věcí je ...
ad Petr Petr: mícháte jablka a banány
Pavel Brož,2015-11-03 23:07:39
Je to bohužel analogické tomu, jako by jedna strana tvrdila, že dokázala, že pokud nějaké ovoce nemá jadérka, tak to nemůže být jablko, zatímco druhá by oponovala, že jejich banány přeci žádné pecičky nemají. Bellovy nerovnosti hovoří o maximální hodnotě určitého specifického výrazu pro lokálně realistické teorie, zatímco Vámi odkazovaný článek pracuje s teorií, která není lokálně realistická. Ba dokonce ta teorie může být stěží označena za klasickou, což vzápětí vysvětlím.
Autoři ve Vámi odkazovaném článku pracují s jednou ze stochastických alternativ kvantové teorie, aplikované na nekoherentní světlo. Existuje celá řada teorií, které se s pomocí stochastických procesů pokouší nahradit kvantovou teorii, což se jim zatím v drtivé většině nedaří. Tím netvrdím, že je něco špatného pokusit se najít alternativu ke kvantové teorii tímto směrem, naopak, každý pokus je legitimní. Výsledky ale bohužel valné nejsou, především pro mnoho kontroverzních výsledků, jako jsou u některých z těchto teorií rozpory se zákony zachování hybnosti či energie, u jiných spory se speciální teorií relativity, jiné výsledky pro dvouštěrbinové pokusy, než dává kvantová teorie, atd. atd.. K tomu připočtěme prakticky nulovou návaznost na další oblasti, ve kterých naopak bez problémů navazuje kvantová teorie. Kvantová teorie totiž na rozdíl od stochastických teorií není omezena např. jenom na optiku nebo jenom na mechaniku, ale také na teorii pevných látek i kapalin, částicovou fyziku, výborně popisuje vedení proudu ve vodičích, supravodičích, či polovodičích, lze ji použít k popisu Boseovských i Fermiovských kondenzátů, k výpočtu vazebných energíí molekul pro prakticky neomezené množství chemických látek, a tak by se dalo ještě hodně dlouho pokračovat. O tak širokém záběru se dnes stochastickým alternativám může jen zdát.
Stochastické teorie navíc velice rády vykrádají matematický formalismus kvantové teorie. Nebo jinak řečeno, samotná stochastická podstata těchto teorií by byla naprosto nedostatečná k vybudování smysluplné teorie, která by uměla popisovat pozorované jevy. Proto se vždy přibere něco z už existujícího bohatého arzenálu kvantové teorie, ať už jsou to Hilbertovy prostory, komplexní pravděpodobnostní amplitudy, lineární operátory či Bornova pravidla. Pokaždé vznikne takový zajímavý kočkopes, který se v důsledku této „hybridizace“ v některých předpovědích s kvantovou teorií naprosto ztotožní, v jiných naopak zcela rozejde. Nebývá proto překvapením, když mnohé z těchto teorií dávají stejně neuvěřitelné předpovědi, jako jsou např. entanglement či vzdálené korelace. Co naopak lze považovat za záhadu, je proč zastánci stochastických teorií tak často označují své výtvory za „klasické“ teorie. Sice samozřejmě si každý může cokoliv označit jakkoliv, mě osobně to pouze přijde podobné, jako označit hip hop za klasickou hudbu.
Podíváme-li se blíže na Vámi odkazovaný článek, lze velice rychle objevit, proč jeho autoři dostávají taktéž hodnoty větší než 2 v Bellových nerovnostech. V rovnici (3) na straně 2 se předpokládá, že stav nepolarizovaného světla je popsán stavem formálně identickým s entanglovaným stavem v EPR experimentu. Protože zbytek matematiky tímto stavem počínaje a výpočtem Bellova výrazu konče, je identický pro obě teorie, tak není žádným překvapením, že obě dají stejný výsledek. Je to jen ukázka toho, co jsem zmínil výše, a to že stochastické teorie si s oblibou vypůjčují části formalismu od kvantové teorie.
Ve Vámi odkazovaném článku se tedy pracuje s teorií, která popisuje nepolarizované světlo formálně identickým způsobem, jakým tak činí kvantová teorie. Co mě přijde jako záhada je proč autoři svoji teorii označují jako klasickou teorii nepolarizovaného světla. Světlo lze totiž popisovat buďto klasicky jakožto elektromagnetické vlnění popisované Maxwellovými rovnicemi. Maxwellovy rovnice jsou skutečnou klasickou teorií světla, ne ten kočkopes popisovaný ve Vámi odkazovaném článku. Klasická teorie světla správně popisuje jevy, jako je interference, difrakce, odraz a lom světla, stejně tak jako mnohé další optické jevy. Maxwellovy rovnice ale neumí vysvětlit existenci kvant světla, tedy fotonů. Fotoelektrický jev byl klasickou teorií světla, tedy Maxwellovými rovnicemi, naprosto nevysvětlitelný, protože podle Maxwellek může světlo o zadané frekvenci nést libovolně malou energii. Tomu ale odporuje experiment, my dnes s jistotou víme, že světlo o zadané frekvenci může nést pouze celé násobky jisté energie, energie nesené právě jedním fotonem.
Vámi odkazovaná teorie popisuje korelaci při detekci fotonů, popisuje tedy kvanta světla. Proč ji tedy autoři nazývají „klasickou teorií nepolarizovaného světla“ když ve skutečnosti popisuje fotony, které jsou klasickými Maxwellovými rovnicemi nepopsatelné, tak to je opravdu analogické jako označit hip hop za klasickou hudbu.
Takže suma sumárum: ve Vámi odkazovaném článku autoři nepoužívají ani klasickou, natož pak lokálně realistickou teorii (mimochodem, o lokálním realismu se v jejich článku autoři vůbec nezmiňují). Pracují s jednou ze stochastických alternativ kvantové teorie, jistým zajímavým hybridem, ve kterém pro popis nepolarizovaného světla z nějakého důvodu používají formálně identický popis, jaký používá kvantová teorie. Také veškerý zbylý aparát až k Bellovým nerovnostem používají identický, proto není divu, že dostávají stejný výsledek jako kvantová teorie. Protože svou teorie z neznámého důvodu označují za klasickou, ačkoliv popisuje kvanta světla (sic!), tak uzavírají, že i klasické teorie mohou narušovat Bellovy nerovnosti. O lokálním realismu ani slovo, ačkoliv ve skutečnosti právě o něj v Bellových nerovnostech jde. Narušení Bellových nerovností je zkrátka a dobře ve sporu s lokálně realistickými teoriemi, ne se stochastickými alternativami kvantové teorie.
A to už vůbec nezmiňuji to, že delftský experiment testoval Bellovy nerovnosti na korelacích měřených na entanglovaných elektronech, nikoliv fotonech, přičemž elektrony výše diskutovaná stochastická teorie vůbec nepopisuje.
Re: ad Petr Petr: mícháte jablka a banány
Petr Petr,2015-11-05 15:52:48
Pěkná přednáška, ale také pěkná tautologie.
"delftský experiment testoval Bellovy nerovnosti na korelacích měřených na entanglovaných elektronech, nikoliv fotonech"
ale
http://arxiv.org/pdf/1508.05949v1.pdf
Stavy byly přenášeny optickými vlákny a nejde přímo o "Stern-Gerlachův" určování spinu elektronů. Měření bylo prováděno optickými detektory atp. Chce to lépe chápat realitu experimentu.
Jabka a hrušky míchají pravě ti, co se snaží obhajovat "kvantové nadpřirozeno".
Pokud mám použít klasické Maxwellovy rovnice, tak zároveň do toho nemohu míchat fotony (to v té teorii vůbec není). Jenže pro dokazování (vyvracení klasičnosti) se použije, že pro úhly polarizátoru 45° dojde k přeskoku v detekci (obdélníková distribuce v závislosti na úhlu). Ale jen v klasických případech (nikoli pro kvantovou teorii). Poté pro korelace (konvoluci mezi úhly) vyjde trojúhelníkový tvar v detekci pro "klasickou předpověď". Jenže čistě klasicky je to pro polarizátory "sinus" (tak jak to předpovídá kvantová teorie), což je (historicky starší) Malusův zákon.
https://en.wikipedia.org/wiki/Bell%27s_theorem
https://en.wikipedia.org/wiki/File:Bell.svg
(Klasicky pro mnoho "fotonů" dostanu stejný výsledek/funkci jako kvantově pro málo "fotonů".)
Suma sumárum, jsou to jen interpretace kvantové mechaniky
https://cs.wikipedia.org/wiki/Interpretace_kvantov%C3%A9_mechaniky
oněch experimentů a nikoli realita.
Re: Re: ad Petr Petr: mícháte jablka a banány
Pavel Brož,2015-11-05 21:51:18
Pane Petr, nikde jsem netvrdil, že v delftském experimentu určovali spiny elektronů Sternovým-Gerlachův přístrojem. To by ani nebylo možné, protože detekce musela být extrémně rychlá. Spiny elektronů se dnes samozřejmě měří mnohem modernějšími technikami, jedna z nich je založená na spinově závislé fluorescenci v NV vakanci v diamantu, a právě ta byla použita v delftském experimentu. Tato technika byla vyvinuta nikoliv pro potřeby testování Bellových nerovností, ale kvůli realizaci kvantových registrů, které jsou velice důležité pro kvantový computing a implementaci kvantových algoritmů, které na klasickém železe nemůžou fungovat. Ronald Hanson a jeho tým se zkrátka zaměřují převážně na praktické aplikace kvantové teorie, a dle jejich výsledků si nevedou vůbec špatně. Test Bellových nerovností byl jenom vedlejším produktem jejich hlavního výzkumu, kterým je převádění kvantových fenoménů do praktického využití.
Každopádně ale to, co se měřilo, byl spin elektronů, nikoliv spin fotonů, a právě z korelací naměřených hodnot spinu elektronů, tedy nikoliv z korelací naměřených hodnot spinu fotonů, počítali ten výsledek. Vámi odkazovaný článek odvozuje maximální hodnoty výrazu figurujícího v Bellových nerovnostech pro nepolarizované světlo, nikoliv pro elektrony, protože tam prezentovaná teorie neumí o chování elektronů říct zhola nic. Takže chce to opravdu lépe chápat realitu toho experimentu, pane Petr.
Co se týče porovnávání Malusova zákona s testováním Bellových nerovností, tak to už je úplně a voze a o koze. Malusův zákon udává intenzitu polarizovaného světla prošlého dvěma polarizátory, které spolu svírají daný úhel. Na obrázku, který odkazujete, je ale závislost korelací v závislosti na úhlu mezi vzdálenými detektory, nikoliv úhlu mezi polarizátory, přičemž navíc jimi žádný společný paprsek neprochází. Prostě u Malusova jevu máme závislost popisující intenzitu světla, zatímco u Bellových nerovností máme závislost popisující korelace vzdálených měření, tedy vynáší se tam naprosto odlišné fenomény. Ale prostě hodinky jako holinky, viďte, koneckonců v obou případech je tam někde k zahlédnutí sinusovka, tak to přece spolu musí nutně souviset, rozumím Vám dobře? Takže kdo tady míchá jabka a hrušky?
Suma sumárum, když něco vygoogluju, tak se nejprve přesvědčím, jestli to má nějakou souvislost s tím, co kritizuju, dříve než to použiju jako argument. V opačném případě nemám šanci se nějaké reality vůbec dobrat.
Re: Re: Re: ad Petr Petr: mícháte jablka a banány
Petr Petr,2015-11-06 09:41:18
Pěkné poučování a tlumočení omáčky autorů (stejně jako v "Osel proti náboženství", kde je také spousta příspěvků).
Já jsem absolvent MFF UK optiky a tak sáhodlouhé textové komentáře považuji o ničem (a myslel jsem, že jste chápavější a ne takový dogmatik).
Korelace souvisejí s koherencí polí (intenzitou)
https://en.wikipedia.org/wiki/Degree_of_coherence
Jak chcete určit spin elektronu měřením fotony? (leda dost nepřímo) Vím, že článek je tak nazvaný, ale vstupem je náhodné elektromagnetické záření (ne elektron), excituje centrum v diamantu, světlo s z něj jde pak optickým vláknem a kombinuje se optickým děličem a výstupem jsou detektory fotonů. Všechny měřené vstupy a výstupy (do výpočtů) jsou optické a nikoli o elektronech (spíš jde o elektronový stav, což ale není elektron). To je podle mého loophole.
Rekapitulace:
Malusův zákon je sinus intenzity na natočení dvou polarizátorů.
EPR paradox (související s entanglementem a nerovnostmi) se měří (v optickém případě, který převažuje) natáčením dvou polarizátorů
https://en.wikipedia.org/wiki/EPR_paradox
např. (ale i jinde)
http://faculty.wiu.edu/BM-Davies/qlab/ajp70_903reed.pdf
a vychází sinus počtu fotonů (intenzita je lineárně úměrná počtu fotonů)
(je jedno o jaké vzájemné úhly jde, protože (konečné) kombinace harmonické funkce dá harmonickou, ale ne trojúhelníkovou závislost)
Neodpovídejte na nic jiného a jen vysvětlete, jak může teorie skrytých parametrů předpovídat onen obdélník a z něj trojúhelník pro průchod polarizátorem v závislosti vzájemném na úhlu.
(odtud pochází ten rozdíl 2,828 vůči 2 a celé ty závěry)
Klasicky, jen Maxwellova teorie (bez fotonů), nedá nikdy (pro intenzity) obdélník, ale sinus. To je loophole interpretace proti skrytým parametrům (respektive lokálnímu realismu). Mícháni klasické teorie (Maxwell) a kvantové (fotony) dá nesmysl, ale to nediskvalifikuje nějakou teorii, ale tento hybrid.
(pokud k jakékoli "správné teorii" přidám jeden nekompatibilní předpoklad, tak z toho vznikne snadno falzifikovatelná teorie)
Re: Re: Re: Re: ad Petr Petr: mícháte jablka a banány
Pavel Brož,2015-11-06 22:33:25
Tak to byste nejspíš měl vrátit vysokoškolský diplom, protože ve Vašich příspěvcích se to katastrofálními neznalostmi jenom hemží. U koho jste prosím Vás tu optiku studoval? Já jsem mimochodem brzy po revoluci úspěšně složil přijímačku na postgraduál u prof. Jana Peřiny, zakladatele olomouckého pracoviště kvantové optiky, určitě jej jakožto absolvent optiky na MFF UK musíte znát, nebo aspoň jeho stejnojmenného syna, který jde úspěšně v otcových šlépějích.
Jádrem Vaší argumentace je, že když A nějak souvisí s B, a B nějak souvisí s C, pak z A musí plynout C (což je samozřejmě nesmysl). Pojďme to rozkrýt, pro přehlednost budu Vaše omyly číslovat.
První ze všeho ale nejprve zareaguji na Váš požadavek, abych vysvětlil, jak může teorie skrytých parametrů předpovídat onen „obdélník“, jak jej nazýváte. Komické na tom je, že právě ukázku takové teorie skrytých parametrů ukazují autoři článku z Vašeho posledního odkazu http://faculty.wiu.edu/BM-Davies/qlab/ajp70_903reed.pdf, a to v části VIII. A LOCAL REALISTIC HIDDEN VARIABLE THEORY. To opět dokazuje, že googlovat sice umíte, ale už si nedáváte práci přečíst to, co jste vlastně vygoogloval, takže ve výsledku používáte odkazy, které nakonec vypovídají proti Vašim vlastním tvrzením :-)))
Nyní ale k těm Vašim omylům:
Omyl č. 1: „EPR paradox se měří natáčením dvou polarizátorů a vychází sinus počtu fotonů“.
Nikoliv. Při testech Bellových nerovností na entanglovaných fotonech se měří korelace mezi detekcemi fotonů v oddělených detektorech. Vůbec se neměří intenzita světla, protože se pracuje s entanglovanými stavy dvou fotonů, kdy v každém z protilehlých směrů jde právě jeden foton. Např. v úplně prvním Aspectově měření na entanglovaných fotonech z roku 1982 každý z obou fotonů následně dopadá na svůj vlastní polarizační hranol, na kterém se musí rozhodnout, jestli projde jedním či druhým směrem odpovídajícím dvěma navzájem kolmým polarizacím. Za každým hranolem jsou dva detektory, zareaguje tedy vždy jen jeden z nich (tím se mimochodem dá také ověřit, že stavy procházející hranolem jsou jednofotonové, právě podle antikoincidence mezi dvěma detektory za každým hranolem). Intenzita světla prošlého hranolem se neurčuje, protože ta může nabývat pouze dvou hodnot – foton prošel nebo foton neprošel. To, co se ve skutečnosti určuje, je koincidence mezi celkem čtyřmi detektory. Tyto koincidence jsou to, co se pak vynáší do grafu.
Omyl č. 2: graf z Vašeho odkazu https://en.wikipedia.org/wiki/File:Bell.svg podle Vás porovnává předpověď kvantové mechaniky (modře) s předpovědí Maxwellovy teorie (červeně), protože argumentujete Malusovým zákonem, kde vychází sinosuvka.
Jednak Maxwellova teorie nejde na dvoufotonové entanglované stavy vůbec použít (a jiné se pro testování Bellových nerovností nepoužívají), protože s jejich existencí vůbec nepočítá. Maxwelky jdou použít jako v jistém smyslu limitní popis pro relativně intenzivní světlo tvořené mnoha fotony, selhávají u popisu velice řídkých svazků tvořených malým počtem fotonů, kdy se projevují právě ty jevy, jako jsou antikoincidence při průchodu řídkého svazku polarizačním hranolem, anebo vztahem pro součin neurčitostí intenzity světla a neurčitosti jeho fáze, a v celé plejádě dalších projevů kvantové optiky. Nikde tam nelze Maxwelky použít, a už vůbec je nelze použít pro předpověď koincidencí mezi detektory jednofotonových stavů.
Ta červená křivka na Vámi odkazovaném obrázku je totiž ve skutečnosti nejoptimálnější hypotetická předpověď, kterou vůbec mohou lokálně realistické teorie dosáhnout, to není předpověď nějaké konkrétní teorie, a už vůbec to není předpověď Maxwellovy teorie, která předpověď pro koincidence detekcí jednofotonových stavů vůbec neumí dát.
Mimochodem, pokud by jednofotonové stavy použité v testování Bellových nerovností nebyly entanglované, ale nezávislé, tak by ta červená křivka byla nulová. Takový experiment se dá velice jednoduše realizovat tím, že každý z dvojice fotonů necháme projít dvěma polarizačními hranoly místo jednoho, a v prvním napevno vybereme polarizaci a fotony s tou druhou zahodíme. První měření zlikviduje entanglement, takže následně už se budou fotony chovat zcela nezávisle, a korelace mezi detekcemi bude nulová, tj. každý z dvojice detektorů bude detekovat nezávisle na výsledcích druhé dvojice.
Omyl č. 3: Vámi odkazovaný graf podle Vás souvisí s výsledky měření pro fotony, protože argumentujete v grafu vynesenými hodnotami pro úhly 45°, 135°, atd., přičemž je srovnáváte s tím, co dává Malusův zákon pro průchod světlem dvěma polarizátory.
Grandiózní omyl. Vámi odkazovaný graf ve skutečnosti dává výsledky pro elektrony, analogický graf pro fotony totiž vychází s největšími odchylkami kvantová versus klasické teorie nikoliv pro úhel 45° (plus násobky 90°), ale pro úhel 22,5° (plus násobky 45°). Je to způsobeno tím, že zatímco elektrony mohou mít průmět spinu pouze +1/2 a -1/2, fotony mohou mít průmět spinu +1 nebo -1. Ve výsledku se to odrazí v tom, že výsledek pro fotony vychází podobný, jako pro elektrony, ale pro dvojnásobný úhel. Pokud by Vámi odkazovaný graf popisoval korelace pro fotony, začínal by shodně pro nulový úhel hodnotou -1, osu by ale protínal pro úhel 45° místo pro 90°, maximum by nabýval pro hodnotu 90° místo pro 180°, atd.. Tedy pro fotony jsou mezi nulami v korelacích rozestupy 90°, kdežto Malusův zákon místo požaduje pro rozestupy mezi nulami 180°. Což je jen další důkaz toho, že pouze vršíte na hromadu vygooglované odkazy, aniž byste si dal práci s přemýšlením nad tím, o čem vlastně vypovídají.
Takže tedy absolvent optiky na MFF UK? Mě optiku přednášel tehdy doc., dnes profesor Pantoflíček, a cvičení jsme měli u tehdy doktora Petra Malého, dnes už je také profesor, četl jste od něj jeho Optiku? Taky je výborná Peřinova knížka Quantum Statistics of Linear and Nonlinear Optical Phenomena, mohu vřele doporučit.
Re: Re: Re: Re: Re: ad Petr Petr: mícháte jablka a banány
Petr Petr,2015-11-07 07:40:46
Stejní učitelé, ale rozdílné výsledky.
(ono na studiích a titulech nezáleží)
Už se nebudu rozepisovat a dále pak reagovat, protože to nemá cenu a nemám na pojednání čas.
Nejsem sám. Korelace druhého řádu nic nevyvrací...
http://arxiv.org/abs/1308.4239
(není to loophole free, i když to neseriózně tvrdí, protože potřebují publikovat)
Re: Re: Re: Re: Re: Re: ad Petr Petr: mícháte jablka a banány
Pavel Brož,2015-11-07 16:49:38
Je mi to opravdu velice líto, ale po přečtení článku z Vašeho posledního odkazu http://arxiv.org/abs/1308.4239 musím konstatovat, že i tento je o něčem jiném, než se domníváte. Jeho autoři se nepokouší napadnout Bellovy nerovnosti, ale zobecnit je na případy, kdy není vyžadován předpoklad, že měření dá pouze dva možné výsledky (tedy předpoklad tzv. dichotomie možných výsledků měření), nebo kdy dá pouze konečnou množinu výsledků v některých dřívějších zobecněních Bellových nerovností. Zmíněný předpoklad dichotomie je splněn v případě měření průmětu spinu elektronu nebo fotonu, kdy lze dostat pouze +1/2 nebo -1/2 pro elektron, či +1 nebo -1 pro foton. Proto testování Bellových nerovností pomocí měření spinu na entanglovaných párech je naprosto v pořádku, a závěr v případě jejich narušení je správný, protože předpoklady jsou zde splněny.
V případě měření jiných veličin, které mohou dávat více možných nenulových výstupů než jen dvě, a zejména pak v případě veličin jako jsou poloha nebo hybnost, které mohou dát nekonečné a spojité spektrum výsledků, nelze Bellovy nerovnosti použít. Autoři Vámi odkazované práce se proto pokusili zobecnit Bellovy nerovnosti tak, aby získali test nezávislý na předpokladu dichotomie výsledků měření, plus aby byl použitelný na obecnějších stavech, než jaké se používají při testování Bellových nerovností. Z tohoto důvodu taky označují testování Bellových nerovností jako tzv. stavově závislé (state-dependent), protože měření se provádí na speciálních dvoučásticových stavech: na nelokálních entanglovaných stavech. Cílem autorů bylo tedy ukázat, že klasické teorie lze ve skutečnosti vyloučit i pomocí obecnějších testů, plus navíc se jim podařilo jeden takový test speciálně pro měření polohy a hybnosti navrhnout.
Není překvapením, že zeslabením předpokladů (v daném případě umožněním použít ne jen nelokální entanglované stavy dvou částic, plus vypuštěním předpokladu dichotomie měření) se získá tvrzení, které je sice univerzálnější, ale má menší výpovědní sílu, než to původní. Můžeme si to ilustrovat na větě: „má-li živočich čtyři nohy a je to obratlovec, tak nelétá a neprochází vývojovými stadii larva-kukla-dospělec“. Představme si, že chceme z předpokladů této věty vypustit požadavek čtyř nohou. Jenže pak také musíme obětovat něco z tvrzení té věty, konkrétně to létání, protože ptáci jsou obratlovci a přitom létají. Získáme tak větu „je-li živočich obratlovec, pak neprochází vývojovými stadii larva-kukla-dospělec“. Tedy získali jsme větu, která je sice obecnější, než předchozí, zato nám toho ale méně vypoví (zeslabení předpokladů zeslabilo i výpovědní sílu věty).
Úplně stejné je to v tom článku, který odkazujete. Pokud použiju předchozí příměr, tak testování Bellových nerovností v něm hraje roli té první věty, která tvrdí: „Měření veličin dávajících jen dva možné výsledky, na nelokálních entanglovaných stavech dvou částic (což je obojí splněno při testování Bellových nerovností), umožňuje vyloučit nekontextuální a lokální (tj. klasické) teorie už na základě porovnání korelací druhého řádu“. Korelace druhého řádu jsou opět ty, které figurují v Bellových nerovnostech, druhého řádu jsou proto, že se porovnávají výsledky získané simultánním měřením dvou pozorovatelů A a B.
Autoři Vámi odkazovaného článku ukázali, že existuje možnost vyloučit jakékoliv nekontextuální a nelokální teorie pomocí korelací čtvrtého řádu, přičemž nepotřebují předpokládat dichotomii výsledků ani pracovat s nelokálními entanglovanými stavy. Také se jim podařilo jeden test konkrétně pro měření polohy a hybnosti navrhnout, musí v něm ale figurovat nejméně čtyři simultánně měřící pozorovatelé A, B, C a D, každý z nich se přitom rozhoduje mezi třemi nastaveními svého přístroje (u Bellových nerovností stačili pouze dva pozorovatelé, a rozhodovali se každý mezi dvěma možnými nastaveními svého přístroje) a pracuje s korelacemi čtvrtého řádu, tedy korelacemi mezi výsledky čtyř nezávislých měření. Původní věta byla tedy nahrazena větou obecnější (protože v ní už nefiguruje předpoklad dichotomie výsledků), ale zároveň větou se slabší výpovědní silou (klasické teorie jsou vyloučeny až pomocí korelací nejméně čtvrtého řádu). Zní tedy: „Měření obecných veličin, i těch dávajících spojité výsledky, jako je např. poloha a hybnost, umožňuje vyloučit nekontextuální a lokální (tj. klasické) teorie na základě porovnání korelací aspoň čtvrtého řádu“.
Takže velice lituji, ale opět jste našel něco jiného, než jste myslel.
Martin Plec,2015-11-03 06:20:44
Na jednu stranu píšete, že pro měřicí přístroj je důležité, aby byl entanglovaný s měřenou veličinou, na druhou stranu píšete, že měřicí přístroj je klasický a v superpozici stavů nemůže existovat. Není mi jasné, kde mezi kvantovým a klasickým přístrojem vidíte rozdíl.
Když budu např. pozorovat auto a jeho směr pohybu promítnutý do osy západ východ. Tak auto se vyskytuje ve stavech |az> (auto na západ) nebo |av>, a měřicí přístroj naměří |mz> nebo |mv>. Stav systému je |az>|mz>+|av>|mv>. Jakmile provedu měření, stav systému zkolabuje např. do |av>|mv>, a každé následující měření toto potvrdí. Když budu už předem vědět, že auto jede z Prahy do Brna, tak vždy naměřím |av>|mv>. V čem tedy tkví ta nekvantovost?
Kromě toho, my sami jsme součástí měřeného systému, takže my můžeme na displeji měřicího přístroje přečíst |čz> (člověk vidí hodnotu západ) nebo |čv>,ale protože jsme dokonalí, tak stav systému člověk - měřicí přístroj je |mz>|čz>+|mv>|čv>. Ale opět, jakmile jednou naměříme |čv>, tak z toho plyne |mv>, a tedy i |av>|mv>|čv>. V čem je tedy rozdíl mezi kvantovým a nekvantovým měřicím přístrojem?
Re:
Pavel Brož,2015-11-03 20:50:24
Klasické systémy nelze entanglovat. Můžete entanglovat kvantovou částici s přístrojem, a pokud tento přístroj bude možno považovat za kvantový systém, pak můžete dostat Vámi popsaný entanglovaný stav |az>|mz>+|av>|mv>, kde |az> či |av> jsou možné stavy kvantového auta. Použitím popisů kvantové mechaniky na klasické systémy lze dojít k mnoha paradoxům, a i když se to občas spíše z didaktických důvodů používá, podobně jako jsem to použil já níže, tak je nutné takové popisy brát s rezervou.
Hranice mezi kvantovým a klasickým systémem je dodnes jedna z nevyjasněných koncepčních otázek kvantové teorie, věnovala se tomu spousta velice chytrých hlav, ale dodnes tento problém zůstává nezodpovězen. Jedna z nejvýznačnějších postav věnujících se tomuto problému je Wojciech H. Zurek (https://en.wikipedia.org/wiki/Wojciech_H._Zurek), který se velice intenzivně zabýval problémy kvantové dekoherence, kvantového měření, kvantového chaosu, hranicí mezi kvantovým a klasickým světem, resp. tzv. "vynořování se klasického světa z kvantového", atd.. Je také autorem velice zajímavé, i když ne úplně všemi přijímané koncepce kvantového Darwinismu, kterou si dost možná odradil některé příznivce, protože znamenala dost podstatný převrat v jeho vlastních názorech, sám jsem se tehdy divil, že vlastně popřel všechno, co za dlouhá léta svého předchozího výzkumu tvrdil.
Nicméně abych se vrátil k Vašemu popisu, on se někdy opravdu používá i na klasické systémy, ale člověk musí umět zkousnout absurdity, které z takového popisu vzejdou. Typickým příkladem je obměna myšlenkového experimentu se Schrödingerovou napůl mrtvou a napůl živou kočkou, které se říká Wignerův přítel. Wignerův přítel je zavřený ve velikém boxu spolu s kočkou, je ale chráněný skafandrem před účinky jedu, který by zabil kočku v případě rozpadu radioaktivního atomu. Zatímco u původního myšlenkového experimentu se samotnou kočkou se získal entanglovaný stav |nerozpadlý atom>|živá kočka>+|rozpadlý atom>|mrtvá kočka>, tak zde by před otevřením boxu měl být sustém ve stavu |nerozpadlý atom>|živá kočka>|veselý Wignerův přítel>+|rozpadlý atom>|mrtvá kočka>|smutný Wignerův přítel>. Podstata té obměny je v tom, že nyní by se měla v propleteném stavu nacházet myslící inteligentní bytost schopná celou dobu pozorovat sama sebe i své okolí. Po pravdě řečeno není to zase až o tolik absurdnější výsledek, než napůl živá a současně napůl mrtvá kočka, jedná se akorát o vyhrocení absurdna toho výsledku.
Je zajímavé, že různí fyzici i matematici se pokoušeli vyrovnat s tímto absurdním výsledkem různě. Podle některých, jako byl třeba John von Neumann či Eugenne Wigner, mělo ke kolapsu vlnové funkce docházet až když v mysli pozorovatele dojde k uvědomění si výsledků měření. Podle jiných už jakýkoliv tvor obdařený vnímáním kolaps vlnové funkce mohl způsobit. Ještě jiní, jako např. Hugh Everett či právě zmíněný Wojciech Zurek k žádnému kolapsu vlnové funkce nedochází, ale celý vesmír se štěpí do všech možných variant odpovídajícím všem možným kombinacím, které fyzikálně mohou nastat.
Přiznám se, že mě samotnému sice přijde myšlenka, že v okamžiku měření dochází ke kolapsu vlnové funkce "v celém vesmíru najednou", jako neuvěřitelná pitomost, ovšem na druhou stranu myšlenka, že se místo toho štěpí celé vesmíry, mě přijde jako nesrovnatelně větší pitomost. Sám k tomu mám pragmatický přístup typu používejme předpovědi kvantové teorie všude, kde to půjde, ale buďme připraveni na to, že jednou narazíme na mez její platnosti, a pak třeba nalezneme nějakou lepší teorii, která zodpoví i dnes nezodpovězené problémy.
Pokud ale zkousneme přechodné absurdity, tak můžeme proces měření kvantového systému klasickým přístrojem popsat právě tím způsobem, jaký jsem níže použil, tj. jako dvoufázový proces, ve kterém v prvním kroku vznikne entanglovaný stav |az>|mz>+|av>|mv> (tedy stav Schrödingerovské kočky, pokud je přístroj makroskopický tak, jako ta kočka), a ve druhém kroku dojde ke kolapsu tohoto "Schrödingerovsko-kočkového" stavu do stavu klasického, např. do |az>|mz>. To dává aspoň formálně smysl, pokud část toho systému je kvantová. Pokud jsou ale obě části klasické, tak to v principu nemůže dávat smysl vůbec.
Re: Re:
Martin Plec,2015-11-03 23:05:00
Děkuji za odpověď. Stále však nerozumím tomu, v čem má být ta odlišnost mezi kvantovým a klasickým systémem (píšete "klasické systémy nelze entanglovat"). Osobně s paradoxem Wignerova přítele - pokud jsem jej správně pochopil - nemám žádný problém, žádnou absurditu tam nevidím. Prostě pokud jsem Wiegner, tak čekám, jak experiment s kočkou dopadne, a stav mého přítele je pro mne záhadou. Ale jakmile vyleze krabice, tak jeho stav zkolabuje (ale zkolabuje jen vůči mně!) a můj přítel bude buď veselý, a nebo bude smutný. Přesně, jak jste to popsal. Píši "vůči mně", protože pro dalšího pozorovatele zůstává stav mého přítele a i můj vlastní stav stále složený (nebo jak se to nazývá), a zkolabuje např. v okamžiku, kdy se dozví můj stav a bude vědět, že můj stav byl se stavem mého přítele provázaný (=entanglovaný).
Možná jste to tu už někde psal, možná je to zřejmé, ale když shrnu předchozí odstavec, tak mi připadá, že provádění měření je vlastně provazování stavů měřeného a měřícího systému. Když můj přítel vyleze z krabice, tak se jeho a můj stav spolu prováží. A i když pro třetího pozorovatele budou stále neznámé (=složené), bude aspoň vědět, že jsou korelované (=provázané).
Kdysi jsem přišel do styku s Feymannovými integrály přes všechny historie vymezené okrajovými podmínkami začátku a konce děje, a taky jsem četl sci-fi o cestách časem. A tak mi nepřipadá vůbec proti mysli, že by všechny možné stavy světa "existovaly" zároveň. Jen jsme provázáni pouze s jedním z nich, a tak ty ostatní nevidíme. (Ve skutečnosti jsme provázáni se spoustou z nich, ale ty se liší jen ve vlastnostech, které zrovna nepozorujeme.) A tak nám svět připadá klasický.
Je tedy nějaký zásadní rozdíl mezi klasickým a kvantovým systémem, který je odlišuje? Třeba něco jako Bellovy nerovnosti, nebo jiná význačná vlastnost?
Re: Re: Re:
Pavel Brož,2015-11-03 23:22:58
V tom myšlenkovém experimentu nešlo o to, jak situaci vidí člověk mimo krabici. Jemu může být fuk, jestli je v krabici v superpozici kočka nebo jeho přítel. Jde o to, jak situaci vidí ten člověk uvnitř. Vy si umíte představit sebe samotného v superponovaném stavu? :-) Já sám sebe neumím! :-)
Zmíněný paradox je totiž paradoxem, v němž je v sázce OBJEKTIVITA fyzikálního popisu. Fyzikální popis by měl být objektivní, tzn. měl by být stejný pro oba pozorovatele, toho uvnitř i toho venku. Místo toho ten uvnitř popisuje situaci zkolabovaným, tj. nesuperponovaným stavem, zatímco ten vně ho popisuje superpozicí. Kde je objektivita, která by měla být fyzikálním teoriím vlastní?
Správná odpověď je ta, že odpověď ještě neznáme :-) Kvantová teorie se v těchto paradoxem zkrátka škaredě topí a uspokojivě je vyřešit neumí. Osobně jsem toho názoru, že bude potřeba až nějaké budoucí, rozšířenější teorie, která nám tu správnou odpověď přinese. Ale tu pravděpodobně nevymyslíme dříve, než začneme narážet na hranice platnosti současné kvantové teorie. Ta se bohužel, potvora jedna, stále ještě velice pevně drží :-)
Re: Re: Re: Re:
Martin Plec,2015-11-04 00:41:14
No, mně to nepochopitelné nepřipadá. Pozorovatel sám pro sebe nikdy v superponovaném stavu není. (Nebo aspoň ne ta jeho část, kterou zrovna pozoruje. Samozřejmě, lze to pitvat až do úrovně, co je to vlastně vědomí ap. Takové pitvání ale, myslím si, interpretaci konkrétního pokusu pozmění jen kvantitativně, ne kvalitativně.)
Jak může být fyzikální popis stejný pro dva pozorovatele, kteří ještě neprovedli měření? Nebo z nichž jeden ještě neprovedl měření? Ale když oba měření provedou, tak už bude jejich popis stejný. V čem je paradox? Připadá mi matoucí, že říkáme superponovaný nebo zkolabovaný stav, ale neříkáme vůči čemu (tj. neuvádíme "souřadnou soustavu"). Kočka je ve zkolabovaném stavu vůči Wienerovu příteli (tj. jejich stavy jsou provázané), ale v superponovaném stavu vůči Wienerovi (a tudíž je v superponovaném stavu vůči Wienerovi současně i jeho přítel). Dokud přítel nevyleze z krabice.
Domnívám se, že problém není v tom zjistit, jaká je správná odpověď, ale v tom vůbec formulovat vhodnou otázku. Obráceně je to snadné - k připravené odpovědi vždy dokážete formulovat otázku, na kterou odpovídá. Např. mohu superponovaný stav v makrosvětě definovat "nevím jak to je" Pokud vám to však příliš připomíná interpretaci kvantové mechaniky pomocí skrytých proměnných, tak můžete vymyslet lepší definici, která bude dávat smysl i v makrosvětě. A pro novou otázku dostanete novou odpověď.
Re: Re: Re: Re: Re:
Pavel Brož,2015-11-04 09:16:25
Takhle, třeba Newtonovská fyzika, ale i speciální či obecná teorie relativity, klasická teorie pole apod. nemají problém s tím, aby popis fyzikální události byl stejný pro dva různé pozorovatele, nehledě na to, že jeden je někde zavřený a druhý nikoliv. Prostě klasické teorie nechápou nedokonalou znalost systému jako legitimní důvod pro to, aby byl popis té fyzikální situace pro oba pozorovatele různý. Tím se samozřejmě nemyslí to, že situace musí být pro oba pozorovatele úplně identická, koneckonců každý z nich je na jiném místě, mohou mít vůči sobě pootočené souřadné osy, mohou se vůči sobě pohybovat různými rychlostmi, a toto všechno se promítne do konkrétní hodnoty fyzikálních veličin, které vůči nim daný systém má. Jde tam ale o to, že po zohlednění těchto odlišností není důvod, aby byl popis fyzikální situace pro oba jiný např. jen proto, že jeden z nich zavře oči. Začal by se třeba Měsíc postupně rozmazávat, pokud by se na něj vůbec nikdo nedíval? Nejkomičtější není tato otázka samotná, ale to, že se v odpovědi na ni neshodnou ani renomovaní kvantoví odborníci.
Osobně si myslím, že by se Měsíc rozmazávat nezačal. Myslím si prostě, že pokus popisovat Měsíc kvantovou teorií je přetažení její aplikace daleko za meze, ve kterých tuto teorii máme dobře prověřenou. Věřím tomu, že někde nastane kvalitativní zlom. Ten sice může být z dnešního pohledu ještě dostatečně daleko, takže není důvod kvantovou teorii nepoužívat tam, kde to dává smysl, ale na druhou stranu není nutné ji hned aplikovat na evidentně klasické objekty, natož třeba na celý vesmír. Myslím, že podobně k tomu přistupoval i Feynman, který kvantovou teorii prakticky neustále používal, ale tvrdil, že se mu otevírá nůž v kapse pokaždé, když slyší o Schrödingerově kočce :-)
Re: Re: Re: Re: Re: Re:
Martin Plec,2015-11-04 13:23:46
Mně to připadá úplně jednoduché, a zdá se mi, že to z nějakého pro mně nepochopitelného důvodu komplikujete. Samozřejmě je možné, že se mýlím, že tak jednoduché, jak si to představuji, to být nemůže, protože...ale proč? Zatím se marně snažím dopátrat, kde by to mé chápání, jak jsem se je snažil popsat, mohlo drhnout. Ale tak daleko, abychom do toho mohli šťourat, jsme se zatím ani nedostali, jelikož předkládáte příklady, v jejichž platnost nevěříte ani vy, ani já. Neberte to ale prosím tak, že vás z toho obviňuji. Evidentně bychom to museli rozebrat do větší hloubky, abychom si porozuměli.
Já si také - stejně jako vy - nemyslím, že by se Měsíc měl chovat nějak zvláštně, pokud se na něj nikdo nedívá. Není možné, aby se teď Měsíc začal chovat jinak, než se choval v minulosti. Každá konkrétní historie musí být vnitřně konzistentní. (To je aspoň jeden z předpokladů, z kterých mé pochopení vychází.) Takže pokud náhodou zpozorujeme, že Měsíc se rozmazává, tak se buď mýlíme, nebo mu fyzikální zákony takové podivné chování (v naší lini historie) povolovaly vždy, pouze my jsme si toho doposud nevšimli. Jinak řečeno, není důležité, jaké podivnosti jsme naměřili, ale musí být v čase i prostoru konzistentní.
Nevím, zda je to srozumitelné. Pokusil jsem se to rozepsat ještě podrobněji, ale pak jsem si řekl, že takový rozvláčný text byste stejně nečetl, tak jsem jej zase smazal a snažil se být stručný.
Re: Re: Re: Re: Re: Re: Re:
Pavel Brož,2015-11-04 19:53:05
Určitě bych to četl, koneckonců sám plodím sáhodlouhé komentáře. Stejně si ale myslím, že se nejspíše rozejdeme na tom, jak lze chápat kvantově mechanický popis. Existuje mnoho navzájem i velice odlišných způsobů, jaký smysl kvantově mechanickému popisu přisoudit - tak např. už v knize Quantum Mechanics and the Particles of Nature z roku 1986 od Anthony Sudburyho je jich popsáno osm, a to tam nejsou zdaleka všechny. Těmto způsobům, jak chápat kvantovou teorii a její popis světa se běžně říká interpretace kvantové teorie. Ty jsou zajímavé v tom, že nejdou experimentálně rozhodnout, protože veškeré měřitelné předpovědi dávají identické, liší se pouze v tom jak si je vyložit. Třeba tzv. kodaňská interpretace dává přednost onomu minimalistickému popisu, který vede ke kolapsu vlnové funkce okamžitě a všude v celém vesmíru, a více se s tím nemaže. Důsledkem je samozřejmě subjektivita popisu světa. Everettovská či správněji DeWittova formulace tvrdí, že svět jde popsat objektivně, ovšem zaplatí za to tím, že se sám pozorovatel rozštěpí do všech možných variant (do varianty "smutný Wignerův přítel s mrtvou kočkou" či do varianty "veselý Wignerův přítel s živou kočkou"). Existuje interpretace převádějící všechny zdánlivě nelogické výsledky kvantové teorie už na úroveň logiky, dá se totiž ukázat, že když místo běžných formálních pravidel matematické logicky zavedeme modifikovaná pravidla (tzv. kvantovou logiku), tak všechno může být formálně OK. Existuje také interpretace, která tvrdí, že kvantově mechanický popis nepopisuje přímo fyzikální svět, ale je popisem jenom našich vědomostí o něm, a vědomosti samozřejmě mohou být subjektivní. Pak je ale zase trochu zvláštní, že naše vědomosti se řídí Schrödingerovou rovnicí. Pro změnu zase tzv. transakční interpretace tvrdí, že všechny podivnosti kvantové teorie žádnými podivnostmi nejsou proto, že kvantové systémy umí komunikovat v čase obousměrně, tedy jak do budoucnosti (např. vysláním nějaké vlny), tak do minulosti. Formálně se opravdu dá ukázat, že při šikovném zavedení této obousměrné časové komunikace paradoxy jako jsou vzdálené korelace odpadnou - ovšem jenom za tu cenu, že zavedete jinou podivnost, totiž právě tu oboustrannou komunikaci v čase.
Osobně si myslím, že tato krize v pojetích kvantové teorie plyne z toho, že nám chybí experimentální data z oblastí, kde kvantová teorie selže. My tam prostě ještě nejsme, tak vymýšlíme šílenosti založené na tom, že si myslíme, že naše dnešní poznání popisu kvantového světa je už definitivní, a proto tento popis protahujeme ad absurdum do situací, ve kterých už třeba vůbec neplatí.
Re: Re: Re: Re: Re: Re: Re: Re:
Martin Plec,2015-11-04 22:44:47
Z vašeho výčtu mi připadá nejbližší asi ta translační interpretace (aniž bych znal její podrobnosti), i když já tam necítím potřebu zavádět nějaké oboustranné komunikace v čase. Potřeba zavádět ty komunikace mi smrdí představou jediné linie historie, jíž je neustále potřeba udržovat v konzistenci. Já si místo toho představuji spoustu alternativních linií historie, o nichž se však nedá říct, že "existují", dokud se nerealizují.
U kodaňské interpretace mi připadá, i když její detaily si již nepamatuji, že v ní musí vznikat paradoxy. A DeWittova interpretace mi nedává žádný smysl, jak jsem už psal dříve. Možná, kdybych si o ní něco nastudoval, tak bych ji pochopil a změnil na ni názor. Ta kvantová logika mi připadá zajímavá, nikdy jsem o ní neslyšel. Ale asi to bude jen matematický formalismus, který nic neosvětluje, jen konstatuje, že to tak je.
Díky za článek a dlouhou diskuzi, spoustu jsem se toho dozvěděl. :-)
Re: Re: Re: Re:
Martin Chabada,2015-11-05 22:40:11
Tak jednoducho treba pripustit fakt, ze realita nie je objektivna, rovnako ako bolo pred cca. 100 rokmi nutne sa zmierit s tym, ze priestor a cas nie su absolutne veliciny.
Moj osobny nazor je taky, ze "objektivna" realita je len statistickym sumarom "subjektivnych" realit jednotlivych pozorovatelov. Je to nieco podobne ako makroskopicky fyzikalne meratelne (a v praxi pouzivane) veliciny teplota a tlak nemaju na urovni molekul zmysel (a to sa pohybuje stale v ramci klasickej fyziky) pretoze su len statisticke hodnoty vyplyvajuce z interakcie obrovskeho mnozstva molekul.
Teda si myslim, ze "objektivna" realita ktoru bezne pozorujeme v makrosvete sa preto javi ako nezavisla na jednotlivych pozorovateloch, lebo je vysledkom interakcie obrovskeho mnozstva pozorovatelov a prispevok jednotliveho pozorovatela je rovnako maly ako prispevok jednej molekuly k vyslednej teplote a tlaku na makroskopickej urovni.
Prechod klasicky system -> kvantovy system by potom bol plynuly - cim viac pozorovatelov mame, tym je prispevok jedneho, konkretneho pozorovatela mensi a tak sa system stava viac "klasickym".
Bellův test
Petr Kavan,2015-11-02 18:37:24
Experimentálně se Bellův test poprvé podařilo provést Johnu Clauserovi v roce 1972.
O tom a dalších věcech kvantové fyziky je velice dobrý dokument:
Tajemný svět kvantové fyziky - Einsteinova noční můra
https://www.youtube.com/watch?v=QT0LbDDyKL0
jen takova hloupost
martin vyroubal,2015-11-02 14:04:48
Me napadlo, co kdyz ten dokonale nahodny smer spinu neni nahodny, ale presne dana "nekonecna posloupnost" se kterou se kazdy "prvek rodi"? Samozrejme je to kravina, ale protoze tomu vubec nerozumim, prijde mi to jako hezka teorie:)
Re: jen takova hloupost
Pavel Brož,2015-11-02 21:43:11
To je možnost, která vždycky v principu existuje, a kterou bohužel principiálně není možné vyloučit :-) Ono ale nezáleží na tom, jestli je směr spinu před měřením náhodný nebo ne. Ve Sternově-Gerlachově experimentu lze předchozím měřením směr spinu do požadovaného směru připravit, a opakovaným měřením ve směru stejné osy navíc potvrdit, že se už ve sto procentech dostává stjná ze dvou možných hodnot. Tak např. úplně na začátku mohl být směr spinu náhodný, takže se měřením např. ve směru osy z dostávaly oba výsledky, +1/2 i -1/2. U každého z nich se ale opakovaným měřením ve směru stejné osy získá opět stejná hodnota, tzn. elektrony, které v prvním měření daly výsledek +1/2, i ve všech následujících měřeních dají vždy +1/2 a nikdy -1/2. Stačí ale pootočit Sternův-Gerlachův přístroj o 90 stupňů, což se dá experimentálně velice snadno povést, a elektrony dají opět rozptyl těch hodnot, ale opět jen v prvém takovém měření, kdežto v následujících měřeních v téže ose už budou opět dávat tytéž reprodukovatelné hodnoty. Zase až do dalšího otočení přístroje o 90 stupňů.
Re: jen takova hloupost
Pavel Bílek,2015-11-02 23:21:41
Existenci takové dopředu dané posloupnosti na úrovni jednotlivých částic právě ten popisovaný experiment pomocí Bellových nerovností vylučuje.
Když si vezmeme do rukou za sebe dva polarizační filtry tak můžeme pozorvat, že jak jimi kroutíme, tak stmívání neodpovídá přímo úměrně úhlu: Když jsou spíše rovnoběžné, tak mají tendenci propouštět víc světla, než by odpovídalo přímé úměře. Když jsou spíše kolmé, tak mají tendenci propouštět míň světla, než by odpovídalo přímé úměře. Největší rozdíl oproti přímé úměře je, když polarizační filtry vzájemně svírají úhel 22,5 nebo 67,5 stupně.
Pro falzifikaci Bellových nerovností se používají měření, při kterých byly polarizační filtry na dvou vzdálených místech náhodně nastaveny tak, že vzájemně svíraly právě úhel 22,5 či 67,5 stupně (říká se jim Bellovské úhly). Průlet polarizačním filtrem nastaví polarizaci oběma fotonům, a od polarizace, jakou foton při dopadu na polarizační filtr má, se odvíjí pravděpodobnost, že jím proletí. Na tom jsou pak postaveny Bellovy nerovnosti. Vysvětluje to kapitolka "Domluva nadsvětelnou rychlostí" na http://www.quantum-mechanics.eu/czech.html
Ukazuje se, že pravděpodobnost průletu fotonu polarizačním filtrem závisí na tom, jak byl náhodně nastaven jiný, vzdálený polarizační filtr, přičemž k nastavení toho jiného vzdáleného polarizačního filtru došlo později, než aby informace o tom stačila přiletět rychlostí světla. Když částice musí respektovat takto danou pravděpodobnost, tak nemůže mít dopředu danou posloupnost.
Re: Re: jen takova hloupost
martin vyroubal,2015-11-03 13:59:45
Aha, tak to jsem nepochopil k čemu Bellovy nerovnosti slouží :)
Re: Re: jen takova hloupost
Pavel Bílek,2015-11-06 16:31:49
Děkuju panu Brožovi za trpělivé vysvětlující komentáře.
Namísto "Na tom jsou pak postaveny Bellovy nerovnosti" jsem měl napsat "Na tom je pak postaveno užití Bellových nerovností", omlouvám se.
Dopředu daná posloupnost na úrovni jednotlivých částic může existovat s tím ovšem, že:
1. U propetených částic je použití posloupností nějakým způsobem kolektivní. Nesmí se zapomenout ani na nerozlišitelnost částic, kdy se například elektron zároveň vymění i nevymění s jiným elektronem a od té doby pak už existují v superpozici stavů, kdy se vzájemně prohodily a zároveň se vzájemně neprohodily.
2. Ty posloupnosti musejí před námi zůstat skryty v situacích, kdy by nám jejich znalost umožnila vytvořit logický paradox (za pomoci přenosu informace nadsvětelnou rychlostí).
Možná by se navíc předpoklad o dopředu daných posloupnostech dostal do nějakých potíží, když by se v rámci složitého fyzikálního děje (kdy se např. jen částečně a nějak "spojitě" měří) měly definovat situace, ve kterých je hodnota z posloupnosti odebrána a použita. Třeba by šlo nechat nějaká složitá provázání kolabovat nějakým dostatečně složitým způsobem, který by od částice v závislosti na úhlu pohledu vyžadoval různý počet použití posloupnosti.
Re: Hezký text
Pavel Brož,2015-11-02 21:46:34
Děkuji za velice vlídné hodnocení :-) Mně naopak při asi pátém pročítání a neustálém překopávání přišel ten můj text tak nečitelný, že jsem moc nedoufal, že to někdo přelouská. Všichni, kteří to zvládli, mají můj obdiv :-)
Opakované měření stejného páru
Martin Plec,2015-11-02 09:01:59
Zůstanou obě párové částice provázané i poté, co strana A i B provedou měření, nebo se tím měřením "entanglement" rozbije? Protože pokud by provázání zůstalo zachované, tak by bylo možné přenášet informaci nadsvětelnou rychlostí. Prostě by vysílající A opakovaně měřil spin částice do té doby, než by naměřil chtěnou hodnotu, a pak by už částici v tomto stavu ponechal. S časovým odstupem by si pak přijímající B přečetl, co mu chtěl A sdělit.
Pod opakovaným měřením mám na mysli: změřím v ose x, a když je výsledek měření nevyhovující, změřím v ose z - čímž předchozí měření efektivně vynuluji - a pak znovu v ose x.
Protože však prý informace nadsvětelnou rychlostí posílat nelze, tak by vzhledem k popsanému mělo platit, že po prvním měření vysílajícího A by měl B vždy naměřit antikorelovanou hodnotu k tomuto prvnímu měření bez ohledu na to, co pak A dál se svojí částicí prováděl (tedy že různě ovlivňoval hodnotu jejího spinu). Je to tak?
Re: Opakované měření stejného páru
Pavel Brož,2015-11-02 21:30:23
Nene, entanglement se už prvním měřením dokonale zničí. Podrobněji jsem to popsal spolu se souvislostí se stavy "Schrödingerovské kočky" ve svém sáhodlouhém příspěvku níže, takže zde už jen odkážu na něj.
Re: Re: Opakované měření stejného páru
Martin Plec,2015-11-03 06:29:00
Jaká je tedy odpověď na mou druhou otázku? Pozorovatel B naměří hodnotu (anti)korelovanou výsledku prvního měření pozorovatele A, bez ohledu na to, jestli pak pozorovatel A ještě svoji částici nějak ovlivňoval?
Re: Re: Re: Opakované měření stejného páru
Martin Ondracek,2015-11-03 10:21:21
Ano, výsledky měření pozorovatele B nezávisí na tom, co se svou částicí provádí pozorovatel A. Pokud pozorovatel A bude provádět opakovaná měření Vámi popsaným způsobem, tak výsledky měření pozorovatele B budou korelovat jen s prvním měřením pozorovatele A a s těmi dalšími už ne.
spin
Pavel Ondrejovic,2015-11-02 07:57:12
blba otazka: chapem spravne, ze elektron moze nadobudnut 8 roznych spinov?
(doteraz som zil v tom, ze len dva :) )
Re: spin
Vojtěch Kocián,2015-11-02 09:05:35
Hmm... Pokud to dobře chápu, tak nikoliv. Elektron může mít svůj spin libovolného "směru", ale při měření (interakci) vždy degraduje do jednoho ze dvou možných stavů. Původní vektor spinu konkrétního elektronu zjistit nedokážeme, ale pokud máme k dispozici soubor, u kterého je zaručen stejný spin všech jeho elektronů, můžeme ho určit statisticky. Stejně jako je možné pomocí polarizačního filtru určit rovinu polarizace světelného svazku, ale u konkrétích fotonů to nejde - ty jen buď projdou nebo neprojdou.
Re: Re: spin
Pavel Brož,2015-11-02 21:27:45
Ano, je to přesně jak píšete. Spin elektronu sice má tři složky dané např. jeho průměty do vybraných os x, y, z. Tyto tři složky jsou ale navzájem nekompatibilní, podobně jako jsou navzájem nekompatibilní např. poloha ve směru osy x a hybnost ve směry téže osy. Pro měření si lze vybrat libovolnou složku, a díky kvantování jejích hodnot (např. na rozdíl od polohy nebo hybnosti, které kvantovány nejsou) lze získat jenom buď +1/2, nebo -1/2 (zatímco pro polohu nebo hybnost lze získat jakoukouliv reálnou hodnotu z nějakého intervalu). Nekompatibilita mezi polohou a hybností se projeví tak, že přesné naměření jedné z těchto veličin dokonale randomizuje měření té druhé, která pak se stejnou pravděpodobností získává všechny přípustné hodnoty. Nekompatibilita mezi složkami spinu se analogicky projevuje tak, že určení hodnoty jedné složky dokonale randomizuje měření zbylých dvou - protože ty ale mohou nabývat jenom hodnot +1/2 nebo -1/2, tak se tato randomizace odrazí ve stejné pravděpodobnosti toho, že se ve směru jiné osy naměří jedna či druhá hodnota.
Pokud máme částice dvě, a pro každou zvolíme kterou složku budeme měřit, tak potom máme čtyři možné výsledky: [+1/2;+1/2], [+1/2;-1/2], [-1/2;+1/2], [-1/2;-1/2], kde v hranatých závorkách je na prvém místě vždy výsledek pro první a na druhém výsledek pro druhou částici.
Re: Re: Re: spin
Josef Hrncirik,2015-11-03 21:55:05
Otázka: Mohu odvážně předpokládat, že když kombinuji nahodile výběr souřadnic tj. rozvíjím (x+y+z)**3 =
x**2+ y**2 + z**2 + 2(xy + xz + yz) pak kvůli neurčitosti antikorelované jsou primárně jen 3 kompatibilní kvadráty a v nekorelovaných 6 smíšených členech se nahodile vyskytne polovina, tj. 3 antikorelované a 3 korelované. Tj. korelovaných bude 1/3?
A pokud by nebyla nekompatibilita (neurčitost), korelovaných by byla 1/2 jako jen z (a+b)**2 ?
(Potěší i odpověď, že vše je naopak.)
Re: Re: Re: Re: spin
Pavel Brož,2015-11-04 08:58:27
Odpověď na Vaši první otázku je opravdu 1/3. Pokud budou dva vzdálení pozorovatelé provádět náhodná měření ve třech osách, na jejichž směru se předem dohodnou (tzn. že jeden pozorovatel nebude mít soustavu vůči druhému pootočenou), tak potom se opravdu v 1/3 případů shodnou - zvolí-li pozorovatel A náhodně osu x, bude jen třetinová pravděpodobnost, že pozorovatel B zvolí stejnou osu, a analogicky tomu bude pro zbylé dvě osy. V jedné třetině případů tedy vznikne antikorelace, v ostatních budou výsledky na sobě dokonale nezávislé. Pozorovatelé mohou tuto antikorelaci potvrdit, pokud se po skončení všech svých měření sejdou, a porovnají si své výsledky spolu s tím, které osy měřili. Když ze svých řad vyseparují zhruba třetinu případů, kdy se náhodně ve volbě os zhodli, tak pro tuto podmnožinu výsledků zjistí dokonalou antikorelaci. Zbytek bude naprosto nekorelovaný, v něm budou jejich výsledky nezávislé jeden na druhém.
Pokud by všechny spinové složky byly navzájem kompatibilní, tedy chovaly by se jako klasická vektorová veličina, nebyl by problém je změřit současně, např. by se místo jednoho Sternova-Gerlachova přístroje použila trojice přístrojů sériově seřazených za sebou, což by nevadilo, protože kompatibilita znamená, že se měření nezávislých veličin navzájem neovlivňuje. Spin by se tedy choval podobně jako např. složky vektoru hybnosti, které vůči sobě jsou kompatibilní i v kvantové teorii, a není tedy problém hybnost jakožto vektor změřit úplně, tj. všechny jeho složky. Pokud by se takto choval i spin, pak by antikorelované byly úplně všechny výsledky, protože zákon zachování momentu hybnosti to vyžaduje.
To rozhození antikorelace při vzdálených měřeních na různých osách je tedy opravdu důsledkem nekompatibility mezi jednotlivými složkami spinu. Spin je prostě v tomto ohledu jiný než třeba ta hybnost.
Re: Re: Re: Re: Re: spin
Josef Hrncirik,2015-11-05 09:05:58
Díky, vysvětlil jste to jednoduše a přesvědčivě, i když moje dotazy a poznámky byly zmatené.
Možná stále někde dělám v úvahách chybu. EPR děj s automatickým entanglementem ze zákonů zachování mi problémy nedělá.
Zapínání či vypínání antikorelace či dokonce jejich šíření (vidím pouze jako formální popis); neberu je jako způsobené volbou osy, ale jako důsledek zrodu páru nesený částicemi (nesoucími realizmus i lokalitu i rychlost a informaci o realitě i když náhodně startující).
Mohu chápat i nekompabilitu měření spinu v různých osách.
Domnívám se ale, že bez znalosti formalizmu KM a optiky nejsem schopen pochopit podstatu Bellových nerovností a proč z nich plyne popření lokálního realizmu či čeho. Vlastně?
Kombinovat vlnové funkce entanglovaných fotonů a aplikovat to na průchod světla polarizačními filtry pochopitelně vůbec nedokážu.
Zakopaný pes je asi v komplikovaném formalizmu a chápání podstaty a výsledku optického měření a jeho "zjevného" rozporu s lokálním realizmem ?či čím vlastně?.
Lokální realizmus v KM je vyvrácen, ale nevím jak, natož proč.
Re: Re: Re: Re: Re: Re: spin
Pavel Brož,2015-11-05 23:01:50
Takhle, ona ta Bellova nerovnost (ve skutečnosti se ale experimentálně testuje její varianta zvaná Clauser-Horne-Shimony-Holtova nerovnost, krátce CHSH nerovnost), je určitým vztahem o maximální hodnotě jistého výrazu, který napíšu níže, který je složen z korelací mezi dvěma oddělenými měřeními, která mohou dát maximálně tři hodnoty: +1, -1 a 0. V případě měření spinu hodnota +1 odpovídá jedné ze získatelných hodnot, např. hodnotě průmětu spinu +1/2, tím pádem -1 bude odpovídat hodnotě průmětu spinu -1/2. V případě spinu elektronu je třetí hodnota, tedy 0, nevyužitá, ale to nevadí. Nerovnost sama je matematickou identitou, je nezávislá na tom, o jaké měřené veličin se jedná, pouze je potřeba tak jako u každé matematické věty dodržet předpoklady, a potom platí důsledek.
Takže máme nějaká oddělená měření, kde na jednom místě měříme veličinu A a na druhém veličinu B, přičemž obě mohou dávat pouze výsledek +1 nebo -1 nebo 0. Nevíme nic o fyzikální podstatě těchto měřených jevů, mohou být deterministické, nebo náhodné, řídit se nějakou vnitřní logikou, nebo nějakým vnějším parametrem. Nic z toho nevíme, pouze jenom musíme z každého z těch oddělených měření dostat vždy výsledek +1 nebo -1 nebo 0.
Dále předpokládáme, že minimálně statistiku našich výsledků ovlivňuje nastavení přístroje, kterým měříme. V případě spinu je to nastavení osy měření, ale opět, nemusí to být spin a natočení detektoru, věta platí obecně. Dále předpokládáme, že výsledek může záviset na nějakém společném neznámém parametru lambda, jinými slovy, že veličina A bude nějakou funkcí:
A=A(a,lambda)
kde a je parametr určující nastavení přístroje měřícího hodnotu A, a lambda je společný parametr. Tedy A závidí na nastavení přístroje měřícího A plus na nějakém společném parametru lambda. Podobně B bude funkcí:
B=B(b, lambda)
kde podobně b je parametr nastavení přístroje měřícího veličinu B.
Možná by se mohlo zdát, že vlastně funkce A a B jsou ty nejobecnější, jaké mohou být, ono tomu ale není tak. Nejobecnější funkce by vypadaly takto:
A=A(a,b,lambda)
B=B(a,b,lambda)
jinými slovy, měření A by záviselo jak na nastavení přístroje měřicího veličinu A plus na společném parametru lambda, ale záviselo by také na nastavení vzdáleného přístroje měřicího tu druhou veličinu. Takovou závislost obecně vyloučit nelze, úplně totiž stačí, když si měřící přístroje budou předávat informaci o svých výsledcích, potom nebude nic špatného na tom, když výsledek měření jednoho bude záviset na nastavení druhého přístroje. Pokud jsou ale obě měření kauzálně oddělena, pak by taková obecná závislost byla neslučitelná s lokálním realismem. Podle lokálního realismu by veličina A neměla záviset na tom, jak někdo vzdálený nastavil přístroj měřící veličinu B, pokud informace o jeho nastavení nemůže včas doputovat k prvnímu přístroji.
Předpokládáme tedy pouze závislost A na a plus lambda a závislost B na b plus lambda. Korelační funkce mezi výsledkem měření A a B potom bude:
E(a,b) = integral{ A(a,lambda) * B=B(b, lambda) * ro(lambda) d_lambda}
kde se integruje hodnoty společného parametru lambda, který má nějaké rozdělení ro(lambda) (tj. integrál z ro(lambda) přes všechny hodnoty lambda musí dát jedničku). Význam výrazu výše je ten, že máme dvě neměnná nastavení přístrojů, první má nastavení a, druhý má nastavení b, uděláme pokud možno co největší počet měření pro náhodné hodnoty lambda, které jsou pospány nějakým statistickým rozdělením ro(lambda), a vypočteme tak míru, nakolik spolu ty dvě hodnoty A a B korelují. Pokud by vyšlo E(a,b)=0, tak jsou měření nekorelované, pokud -1, tak jsou dokonale antikorelované, pokud 1, tak jsou dokonale korelované. Hodnota E(a,b) ale samozřejmě může vyjít i jiná, vždy to ale bude reálné číslo z intervalu [-1;+1].
Nyní zkonstruujeme výraz:
S=E(a,b)-E(a,b´)+E(a´,b)+E(a´,b´)
kde a a a´ jsou dvě možná nastavení přístroje měřícího A, a b a b´ jsou podobně dvě možná nastavení přístroje měřícího veličinu B. Máme tedy čtyři možná nastavení naší dvojice přístrojů ((a,b), (a,b´), (a´,b), (a´,b´)), a musíme pro každé z těchto čtyř nastavení udělat reprezentativní řadu měření.
Zbytek už je čistá matematika, viz https://en.wikipedia.org/wiki/CHSH_inequality , kde je dokázáno, že za předpokladů výše uvedených nemůže být absolutní hodnota výrazu S větší než 2.
Právě toto je na těch Bellových, potažmo CHSH nerovnostech tak zajímavé – ony totiž vůbec nic nepředpokládají o fyzice těch měření, ony pouze požadují, aby měření veličiny A sice mohlo být ovlivněno přístrojem měřicím tuto veličinu, a případně nějakým dalším společným parametrem lambda, ale aby nemohlo být ovlivněno nastavením toho druhého přístroje. Podle klasické fyziky by tomu tak u kauzálně oddělených měření mělo být. Jenže podle výsledků testování Bellových nerovností je tomu jinak. Výsledem pro výraz S vyšel výrazně větší než 2. To může znamenat pouze to, že matematické předpoklady použité pro to odvození nebyly splněny.
Re: Re: Re: Re: Re: Re: Re: spin
Josef Hrncirik,2015-11-06 21:04:42
Díky za tuto seminární práci. Je to věcné, přehledné a pádné. Cítím že to je pravda.
I ten formalizmus s trochou vypětí dokážu zkontrolovat a optice či KM se mohu dočasně vyhnout.
Ztrátu lokálního realizmu v KM zatím intuitivně chápu jako rozpliznutí vlnových balíků měřených "částic" v homogenním (symetrickém) vlnovém poli prostředí s nezbytnými neurčitostmi a fluktuacemi. Výsledek je pak relativně lokální a má v sobě zdánlivě "okamžité nelokální" interference A s B, pochopitelně kauzální a "částice i výsledek skutečně "stvoří" pouze akty měření".
Bez nadsvětelných strašidel či vědomí.
Dotaz: Je možno změřit spin aniž ho n *krát převrátím
Josef Hrncirik,2015-11-06 21:16:10
Tj. zda n = 0, 1, 2, ...
či to měřím změnou (ami) v jiných osách?
ev. zda to v KM vůbec nedává smysl?
Re: Dotaz: Je možno změřit spin aniž ho n *krát převrátím
Pavel Brož,2015-11-06 22:57:27
Musím se přiznat, že sice dokážu odvodit ty paradoxy plynoucí z entanglementu na základě formálního aparátu kvantové teorie, ale vnitřně se s tím stále neumím vyrovnat. Ztráta principu lokálnosti ve fyzikálních teoriích je něco, co mi pocitově docela vadí. Představa, že fyzikální procesy se mohou nelokálně ovlivňovat způsobem popsaným kvantovou teorií ve mě evokuje představu jakési magie, a na tu nevěřím. Stejně tak nevěřím na neustálé štěpení vesmírů na základě kdejaké i sebenicotnější interakce, přijde mi to jako plýtvání vesmíry k tomu, aby se něco popsalo v tom jediném vesmíru našem, ve kterém právě my žijeme, nikoliv ve kterých žijí naše hypotetické klony prožívající jejich alternativní historie. I představa kolapsu vlnové funkce okamžitě a v celém vesmíru mi přijde nestravitelná.
Snad nejspokojenější bych byl, pokud by se v budoucnu objevila nějaká "brzda", něco jako nějaká analogie principu neurčitosti, která by sice tyto nelokálnosti dovolovala, ale jen na vzdálenosti, kdy se zase musí minimalizovat něco jiného, aby to jako nemohlo přerůst přes hlavu. Ale to je jenom taková moje momentální zoufalá představa :-) Kvantový svět je prostě šílený, zlatá teorie relativity i s jejími dilatacemi prostoru a času i černými a červími děrami :-)
Bežnosť či vzácnosť entanglementu
Marek Fucila,2015-11-02 03:28:16
Vďaka za skvelý a zrozumiteľný článok!
Mal by som otázku k previazanosti častíc.
V experimente previazali dva páry elektrón-fotón, a potom cez tie dva fotóny aj elektróny. Teda usudzujem, že je nejaká množina podmienok, pri ktorých dochádza k previazaniu. Tipujem, že sú situácie, kedy sa naopak previazanie interakciou stráca. Z toho, že to previazanie bolo 92% to vyzerá tak, že previazanie môže byť viac alebo menej efektívne.
Je možné nejako kvantifikovať, ako sú previazané časice v reálnom svete mimo špeciálnych podmienok experimentu? Či je také previazanie vzácnou udalosťou, ktorá bežne rýchlo skončíkeď fotón do niečoho narazí, alebo naopak takto spôsobí poprepájanie množstva častíc zrejme naprieč celým vesmírom.
Teda či žijeme vo svete, kde sa z času načas niečo previaže ale v zásade to rýchlo zanikne, či je to tu naopak "zdrátované" skoro všetko, alebo niečo medzi tým.:-)
Ak by to bol relatívne bežný stav, potom by ten efekt motýlych krídiel z deterministického systému dostával v kvantovom svete nový rozmer: zamávanie motýlimi krídlami v Brazílii môže spôsobiť zamávanie krídlami iného motýľa v Texase.:-)
Zajímavá otázka
Vojtěch Kocián,2015-11-02 13:15:01
Entanglement jde ruku v ruce se zákonem zachování momentu hybnosti (pro spin, nevím jestli jde provázat i něco jiného), takže pokud (libovolnou) částici změřím, její spin se nějak nastaví a tedy musí existovat částice, jejíž spin se v ten okamžik nastaví obráceně. Moje laická intuice mi říká, že každá částice má svůj provázaný protějšek, ale tato vazba bude mít v běžném prostředí krátkého trvání a interakcemi se bude předávat z částice na částici (taková hra na babu s provázky :-)). Ale může to být i úplně jinak.
Re: Bežnosť či vzácnosť entanglementu
Pavel Brož,2015-11-02 21:12:59
Otázka, zda je entanglement běžnou záležitostí, je velice zajímavá, a po pravdě řečeno se na ní dá odpovědět ano i ne. Odpověď ano platí ve smyslu, že při částice se svými běžnými interakcemi vzájemně entanglují, a že tento proces je velice běžný. Odpověď ne platí ve smyslu, že nelokální korelace vzešlé z takového entanglementu makroskopicky nepozorujeme.
Musím maličko poopravit tvrzení pana Kociána, že entanglement jde ruku v ruce se zákonem zachování momentu hybnosti. Ve všech případech v článku jsem sice popisoval provázání spinových stupňů volnosti, ve skutečnosti jdou ale provázat libovolné stavy. Definice entanglementu je matematicky velice jednoduchá, dvoučásticový systém musí být v tzv. nefaktorizovatelném stavu. Faktorizovatelný stav je popsán jako formální součin stavu jedné částice se stavem druhé částice. Tak např. pokud je částice A ve stavu |psi> a částice B ve stavu |fi>, tak stav systému složeného z obou částic je popisován stavem |psi> |fi>. Tato situace není principiálně nijak odlišná od popisu v Newtonovské fyzice – tam stav částice popisujeme zadáním její polohy a hybnosti. Určíme-li stav, tedy polohu a hybnost první částice (což je celkem šest hodnot), a stav, tedy polohu a hybnost druhé částice (což je dalších šest hodnot), tak známe stav systému těchto dvou částic, který je popsán celkem dvanácti hodnotami. Matematickou terminologií můžeme říct, že stavový prostor dvou Newtonovských částic (což je dvanáctirozměrný prostor potřebný pro zadání všech potřebných poloh a hybností) získáme jakožto kartézský součin stavového prostoru první částice (což je šestirozměrný prostor) se stavovým prostorem druhé částice (což je opět šestirozměrný prostor).
V kvantové mechanice na rozdíl od Newtonovy mechaniky nemůžeme pro popis stavu částice použít trojici hodnot polohy spolu s trojicí hodnot hybnosti, protože tomu brání Heisenbergův princip neurčitosti, který tvrdí, že určíme-li polohu, tak totálně rozmažeme odpovídající složku hybnosti. Můžeme ale částici popsat tzv. vlnovou funkcí určující amplitudu pravděpodobnosti výskytu částice v daném bodě, nebo obecně tzv. stavovým vektorem. Jeden a tentýž stavový vektor totiž můžeme reprezentovat různými způsoby, vlnová funkce je jen jeden z nich – místo ní můžeme použít např. její Fourierův obraz, ten popisuje částici pomocí distribuce hybností, které lze naměřit. To odpovídá tomu, když se místo mapování pravděpodobnosti polohy částice zaměříme na mapování pravděpodobnosti hybnosti částice (tzn. že v prvém případě zjišťujeme distribuci polohy částice pomocí obrazu, který vytvoří např. na detekční fotografické desce či který postupně zaznamenáme ze záblesků na scintilačním stínítku, zatímco ve druhém případě pro změnu mapujeme hybnosti částice např. pomocí rychlostních filtrů). Může se zdát divné, že se dá zjišťovat distribuce polohy částice i distribuce hybnosti částice, protože to může vypadat jako spor s Heisenbergovým principem neurčitosti. Žádný spor tam ale není, Heisenbergův princip neurčitosti pouze říká, že čím užší „pík“ bude v distribuci polohy, tím širší bude v distribuci hybnosti, a naopak.
Zatím jsme popsali pouze faktorizovatelný stav dvou částic. Ten nefaktorizovatelný (tedy entanglovaný) je takový, že jej nelze popsat jedním součinem dvou jednočásticových stavů, ale musí se vzít superpozice nejméně dvou takových součinů. Entanglovaným stavem je tedy např. následující dvoučásticový stav:
|psi1> |fi1> + |psi2> |fi2>
kde |psi1> a |psi2> jsou dva možné stavy první částice, a podobně |fi1> a |fi2> dva různé stavy druhé částice. Pokud jsou stavy |psi1> a |psi2> tzv. ortogonální (to je tehdy, když popisují jakékoliv dva navzájem se vylučující výsledky měření, např. hodnotu spinu +1/2 a hodnotu spinu -1/2), a pokud jsou stejně tak ortogonální i stavy |fi1> a |fi2>, tak potom je entanglement dvou částic maximální.
To je zároveň odpověď na otázku kvantifikace entanglementu. Entanglement dvou částic je maximální, pokud se dají popsat právě zmíněným nefaktorizovatelným dvoučásticovým stavem |psi1> |fi1> + |psi2> |fi2>, kde navíc |psi1> je ortogonální k |psi2> a |fi1> je ortogonální k |fi2>. Naopak entanglement dvou částic je nulový, pokud je dvoučásticový stav popsatelným faktorizovatelným částicovým stavem |psi> |fi>.
Zmíněný stav maximálního entanglementu |psi1> |fi1> + |psi2> |fi2>, kde |psi1> je ortogonální k |psi2> a |fi1> je ortogonální k |fi2>, má velice zajímavou vlastnost. Pokud se měřením zjistí, že první částice je ve stavu |psi1>, tak z toho podle pravidel kvantové teorie automaticky plyne, že druhá částice musí být ve stavu |fi1>. Pokud naopak měřením zjistíme, že první částice je ve stavu |psi2>, tak z toho automaticky plyne, že druhá částice je ve stavu |fi2>. Tuto vlastnost nazvu čistě jenom pro účely tohoto komentáře jako „korelační vlastnost entanglementu“. Zároveň s určením stavu první částice dojde ke zničení entanglementu, protože po měření je systém ve stavu |psi2> |fi2>, tedy ve faktorizovatelném stavu.
V článku popisovaný entanglement je jen speciálním případem, kdy |psi1> odpovídá hodnotě vybrané spinové složky +1/2, zatímco |psi2> hodnotě -1/2, zatímco pro |fi1> a |fi2> je to obráceně, tj. |fi1> odpovídá hodnotě -1/2 této složky a |fi2> hodnotě +1/2.
Takže vidíme, že entanglement existuje pro naprosto obecné jednočásticové stavy, nejen pro stavy odpovídající nějaké konkrétní hodnotě spinu, jinými slovy provázat lze částice v jakémkoliv stavu.
Vraťme se ale k otázce běžnosti entanglementu. K provázání dochází úplně běžně např. při měření prováděném na nějaké kvantové částici. Představme si nejprve, že měřící přístroj popisujeme jako kvantový systém, potom v procesu měření dojde k vytvoření stavu:
|psi1> |fi1> + |psi2> |fi2> + |psi3> |fi3> + ... + |psiN> |fiN>
kde |psi1> až |psiN> jsou stavy odpovídající vzájemně se vylučujícím hodnotám nějaké zvolené proměnné (tedy jsou to vzájemně ortogonální stavy), a |fi1> až |fiN> jsou odpovídající stavy měřeného přístroje. Použitím výše zmíněné „korelační vlastnosti entanglementu“ dostaneme, že pokud zjistíme, že přístroj je např. ve stavu |fi3>, tak částice musí být zase ve stavu |psi3>. To je také požadovaná vlastnost ideálního měřícího přístroje, protože my chceme, aby to co ukazuje, odpovídalo vlastnosti měřeného subjektu.
Zatím jsme měřicí přístroj popisovali jako kvantový systém, my ale reálně měříme na klasických měřicích systémech. Rozdíl mezi kvantovým a klasickým systémem je ten, že ten kvantový může existovat v superpozici stavů, zatímco ten kvantový ne. My umíme připravit např. částici v superpozici dvou různých spinových stavů, anebo třeba v superpozici různých energetických stavů. My ale neumíme připravit klasický měřicí přístroj v superpozici, která odpovídá několika různým naměřeným hodnotám zároveň. Takový stav by byl naprosto ekvivalentní tzv. stavu „Schrödingerovské kočky“, který odpovídá superpozici živé a mrtvé kočky. Tak, jako reálně kočka nemůže být živá a mrtvá zároveň, tak stejně tak klasický měřicí přístroj nemůže ukazovat zároveň navzájem se vylučující hodnoty.
Otázka, kdy a proč se kvantový systém stane klasickým, je dodnes neuzavřenou kapitolou bádání v kvantové teorii. Zkrátka a dobře, měření publikované delftskými výzkumníky předminulý týden sice uzavřelo jednu z důležitých otázek v kvantové teorii, zdaleka ale neuzavřelo všechny otázky, které v ní vznikají, a otázka hranice mezi kvantovým a klasickým světem, ač na toto téma byly sepsány už tisíce prací, zůstává dodnes otevřeným problémem kvantové teorie. Jiným takovým neuzavřeným problémem je otázka tzv. kolapsu vlnové funkce. Tak např. výše jsme zmínili, že pokud vezmeme entanglovaný stav |psi1> |fi1> + |psi2> |fi2> a naměříme na první částici stav třeba |psi1>, přejde systém do neentanglovaného stavu |psi1> |fi1>. Jakým způsobem k tomu přesně dojde dodnes nevíme, pouze to odbýváme tvrzením, že k tomu dojde „okamžitě“ a „všude“, tj. v celém vesmíru současně. To je dost odvážné tvrzení, bez ohledu na to, že naše měření nelokálních korelací opravdu prokazují, že tyto zvláštní jevy existují. Ale musí být opravdu jediná správná odpověď, že ke kolapsu vlnové funkce dochází „v celém vesmíru současně“?
Zmíněné provázání mezi měřeným systémem a měřicím přístrojem je tedy požadavkem na měřicí přístroj. Pokud by k takovému provázání nedocházelo, tak bychom příslušný měřicí přístroj prohlásili za vadný a vyhodili ho, protože by prostě mohl ukazovat něco jiného, než co by měl, tedy jinou hodnotu, než která odpovídá měřenému systému.
Toto provázání obecně likviduje interferenci, což se dá snadno dokázat z pravidel kvantové teorie. Nemusí přitom jít o provázání mezi měřeným systémem a přístrojem, jedná se obecně o vlastnost jakéhokoliv entanglementu, kdy místo měřícího přístroje figuruje druhá částice. Likvidace interference entanglementem je ukázkový příklad, kdy jeden kvantový jev, v daném případě entanglement, potlačuje jiný kvantový jev, v daném případě interferenci. V tom také vězí ona záhada slavného štěrbinového paradoxu, že když se „díváme“ kterou štěrbinou částice prošla, tak interference na stínítku nevznikne, zatímco když se „nedíváme“ tak vznikne. Ve skutečnosti jde jen o to, jestli se vytvoří nebo nevytvoří entanglement prolétající částice s detektorem sledujícím průlet nějakou štěrbinou. Pokud detektor vypneme, tak interakce částice s ním by měla být zanedbatelná, ideálně nulová, proto entanglement nevznikne vůbec, anebo jenom „v malé míře“ (viz míra entanglementu výše). Naopak při zapnutém detektoru (ten může být reprezentován i např. jen osvětlujícím laserovým paprskem) entanglement vznikne a interferenci zničí.
V obecném případě se částice svými interakcemi běžně entanglují, a tento entanglement více a více ničí interferenční jevy, které by teoreticky mohly být v počátečním stavu přítomny. Entanglement sám je ale ale ničen měřením, ve kterém dochází k onomu kolapsu vlnové funkce, procesu, který kvantová teorie běžně používá ve svých předpovědích, o kterém toho ale říká strašně málo, vlastně skoro vůbec nic, kromě toho, že probíhá „v celém vesmíru současně“.
Proto je odpověď na otázku běžnosti entanglementu takováto: máme-li hodně částic, které spolu interagují, tak se navzájem svými interakcemi entanglují, přičemž likvidují interferenci. Od určité velikosti výše pak soubor takových částic přeroste (dodnes nejasnou) hranici mezi kvantovým a klasickým systémem, kdy nemůže existovat ve stavu superpozice (tedy ve stavu „Schrödingerovské kočky“) a zkolabuje (dodnes nejasným způsobem) do jednoho z klasických makroskopických stavů.
Ono ale je to nakonec lepší, že makroskopické entanglované stavy nepozorujeme. Představte si, že by se někomu stalo, že by jeho tchyně např. uklouzla na šlupce od banánu, načež by se ozval rámus z garáže, kde by se dotyčnému současně rozpadlo zánovní auto, se kterým by se tchyně předtím zlomyslně entanglovala právě pro případ, že by šlápla na narafičenou šlupku od banánu. Zajisté uznáte, že v takové situaci by onen nešťastník zažíval entanglované pocity :-)
Re: Re: Bežnosť či vzácnosť entanglementu
Martin Ondracek,2015-11-03 10:13:21
Drobná oprava příspěvku výše: Ve větě "Rozdíl mezi kvantovým a klasickým systémem je ten, že ten kvantový může existovat v superpozici stavů, zatímco ten kvantový ne." mělo být na konci věty správně "zatímco ten klasický ne". Ten kdo ví, o co jde, tak si to samozřejmě domyslí, ale protože článek a diskuze jsou především pro poučení čtenářů, kteří kvantovou fyziku neznají a na jednom takovém překlepu by se mohli totálně ztratit, považoval jsem za vhodné to uvést na pravou míru.
Re: Re: Re: Bežnosť či vzácnosť entanglementu
Pavel Brož,2015-11-03 19:51:37
Ano, omlouvám se za tento omyl, předpokládám ale, že z logiky celého souvětí byl patrný. Během psaní mě občas v půli věty rozptýlí domácí zvířena, pokud dojde k závěru, že bych se měl zase chvíli věnovat jim, takže doufám že jsem podobných nesmyslů nenasekal více :-) Určitě budu rád za každé upozornění na jakoukoliv podobnou nelogičnost.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce