Kvantový zauzlený soliton. Kredit: Heikka Valja.

Touha vázat si uzly podle všeho nemá hranic. Očividně je vlastní i fyzikům, kteří již celá desetiletí předpovídali, že bude možné vytvořit kvantové uzly, čili uzly ve kvantových polích. Až doteď to ale nikdo nezvládl. Bylo to jako lovit exotické příšery, abychom je mohli opatrně prozkoumat a žasnout nad jejich podivnostmi, ale marně.

Mikko Möttönen. Kredit: Aalto University.

Nakonec jako první uspěl finský fyzik Mikko Möttönen z Aaltovy univerzity v Helsinkách, který se svými kolegy kvantové uzly skutečně vytvořil a mohl se jimi pokochat. Teď jsou prý nažhavení na jejich výzkum a očekávají nové objevy, které budou velmi zajímavé pro kosmologii, fúzní energetiku nebo kvantové počítače. Jejich výzkum se dočkal publikace v novém čísle časopisu Nature Physics.

Zařízení na vázání kvantových uzlů. Kredit: Marcus DeMaio / Amherst College.

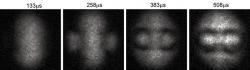
Jak takové kvantové uzly vlastně vypadají? Zapomeňte na zauzlované tkaničky dětských tenisek, i když ty někdy kvantový chaos velice připomínají. Kvantové uzly existují ve kvantovém poli, ve němž vytvořily topologicky stabilní strukturu z prstenců, které nelze oddělit, aniž by došlo k narušení těchto prstenců. Jinak řečeno, kvantové uzly nelze rozvázat, dokud nedojde ke změně stavu kvantové hmoty. Möttönen a spol. vlastně vytvořili zauzlené solitony, čili prostorově lokalizované vlny, ve kvantově mechanickém poli slavného Boseho-Einsteinův kondenzátu z atomů rubidia, zmražených k absolutní nule.

Zauzlování kvantových uzlů v experimentu. Kredit: David Hall.

Vytvoření kvantových uzlů netrvalo nijak moc dlouho. Möttönen s kolegy si připravili speciální magnetické pole a s jeho pomocí zavázali kvantové uzly za méně než tisícinu sekundy. Když zvládli zauzlit první kvantový uzel, tak už jim to šlo jako po másle. Do této chvíle už prý vytvořili stovky takových kvantových uzlů. V běžném životě se setkáváme s uzly, které bývají navázané na provazech či drátech o dvou koncích.

Vizualizace struktury kvantového uzlu. Kredit: David Hall.

To ale není případ uzlů, o nichž matematici říkají, že jsou topologicky stabilní. Stabilní uzly jsou zauzlované tak, že konce „provazu“ či jiného materiálu jsou spojené dohromady a topologicky stabilní uzly tudíž nelze rozvázat bez přeříznutí onoho provazu.

Möttönen a spol. vytvořili topologickou strukturu kvantových uzlů, jako takzvanou Hopfovu fibraci (Hopf fibration). Hopfovu fibraci, která připomíná komplexní zauzlení mnoha prstenců, objevil v roce 1931 Heinz Hopf a matematici i fyzici ji stále ještě studují. Möttönenův tým ji poprvé v historii demonstroval ve kvantovém poli. Topologické vychytávky nejsou každému úplně blízké, a alespoň zběžné pochopení toho, co Hopfova fibrace vlastně je, vyžaduje jisté úsilí. Nemáme ale důvod nevěřit Möttönenovi, že jsme na samotném počátku vzrušujícího příběhu kvantových uzlů. Časem bychom se mohli dočkat ještě sofistikovanějších verzí těchto uzlů a dozvědět se z nich pozoruhodné věci o fungování kvantových polí.

Video: Tying Quantum Knots - Amherst College and Aalto University

How Can CQE Contribute in Advancing Large-scale Quantum-enhanced Computing?


Literatura
Aalto University 18. 1. 2016, New Scientist 18. 1. 2016, Nature Physics online 18. 1. 2016, Wikipedia (Hopf fibration).