Prvního dne tohoto roku jsem v článku na Oslovi rekapituloval výsledky urychlovače LHC na konci roku 2009, kterých se podařilo docílit během jeho opakovaného spouštění. Konstatoval jsem také, že během prvních měsíců tohoto roku se bude urychlovač intenzivně připravovat na urychlování protonů na energie 3,5 TeV.
Připomeňme si v čem je hlavní problém. Na kruhové dráze drží nabité částice (v našem případě protony) v kruhovém urychlovači magnetické pole. Aby i při růstu energie urychlovaných částic zůstal poloměr jejich kruhové dráhy stejný (v případě LHC je to zhruba 4,24

Pro předcházení podobným nehodám, museli technici udělat řadu změn a opatření. Ještě pečlivěji se musely zkontrolovat spoje mezi jednotlivými magnety. Citlivější diagnostika má přispět k rychlejší identifikaci problému na spoji a včasnému vyvedení energie z magnetu. Větší počet a efektivita ventilů má pak umožnit rychlé vypuštění helia vypařeného v případě nehody, aby nedošlo k mechanickému poškození magnetů. Největší část těchto změn byla provedena v minulém roce a podrobně jsem je už na Oslovi popisoval. Koncem minulého roku tak mohl být urychlovač LHC spuštěn a dosáhnout také energie protonů 1,18
V současné době je provoz magnetů v režimu potřebném pro urychlování na 3,5
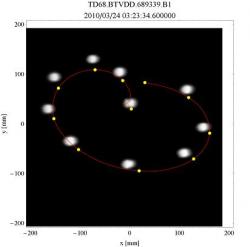
Pokud by měl standardní plánovanou intenzitu, tak by mohlo dojít k vážnému poškození některé z částí urychlovače. Nebezpečí hrozí i detektorům. Pokud se část svazku strefí do nevhodného místa, může dojít k zasažení detektorů velkým množstvím částic. To může vést u některých z nich, pokud jsou pod napětím a v činnosti, k poškození až zničení. Proto jsou některé, zvláště ty nejvnitřnější detektory, během testování urychlování svazku vypnuty. Jednotlivé detektorové systémy tak musí před startem srážek při takto vysokých energiích a před postupným zvyšováním intenzity svazku také ověřit všechny své bezpečnostní procedury.
V úterý 30. března zhruba v 9:17 se očekávají první srážky protonů s energií 3,5
Jak je to se sčítáním energií a rychlostí v relativistické fyzice?
Nyní bych se věnoval otázce relativistických transformací různých veličin. Vyšel bych z diskuze pod článkem Nové výborné zprávy z urychlovače LHC, kde se objevila tato poznámka:
„Hezká příležitost vysvětlit relativistické vztahy. Pan Wagner prostě sečetl 1180 + 1180 = 2360 GeV tak, jak by to udělal každý newtonovský šťoural do relativity. Vždyť přeci letí proti sobě, tak je to jasné! Kde jsou ale relativistické změny hmotnosti s rychlostí? Srážka jednoho protonu s druhým je výsledkem vzájemné rychlosti. Tak by se asi měla měřit a relativisticky vyhodnotit rychlost a tedy hmotnost protonu A z hlediska protonu B, nebo ne?“
Někdo z dalších diskutujících sice vysvětlil, že opravdu v tomto případě i v relativistických vzorcích se pro získání celkové energie v systému energie, které mají jejich části, prostě sečtou a platí zákon zachování energie (pochopitelně i zákon zachování hybnosti) v dané souřadné soustavě, ve které měříme. Přesto bych se pokusil trochu více přiblížit, jak je to s těmi transformacemi rychlostí, energií a hmotností. Už proto, že to i další čtenáře zajímá, jak je vidět s dalšího příspěvku v diskuzi:
„Dalo by se říct, že svazek iontů "vidí" ten druhý svazek, letící proti němu, "těžší"? Nějak mi nejde do hlavy, že letí dva svazky proti sobě rychlostí skoro "c" a srazí se rychlostí zase jen skoro "c", tak si říkám, že někde se ta energie musí projevit - když ne v rychlosti, tak v hmotnosti. Takže zpět k dotazu - dalo by se říct, že jeden svazek "vidí" ten druhý, letící proti němu, "těžší"?“

V předchozím textu jsem několikrát zase sčítal energie dvou srážejících se protonů, abych dostal energii dostupnou ve srážce. Podívejme se, jak tedy vypadá situace v našem případě srážení dvojice protonů, které byly urychleny na energii 3,5 TeV. Jestliže se mluví o energii urychlovaných částic, má se většinou na mysli jejich kinetická energie. V našem případě jsou ovšem kinetická a celková energie urychlených protonů téměř stejné. Celková energie protonu je totiž dána součtem kinetické energie a klidové energie. Klidová energie je ta, která známým Einsteinovým vztahem souvisí s jeho hmotností v klidu. Proton má klidovou energii zhruba 1
Jak je to s hmotností? Klidová hmotnost, stejně jako klidová energie, se nemění s tím, jestli se částice pohybuje nebo ne. Je to jedna z tzv. invariantních veličin, které se v relativistické fyzice nemění při přechodu z jedné souřadné soustavy do druhé. Takových veličin je více a jsou velmi výhodné při počítání relativistických úloh. Jak je to s relativistickou hmotností? Mezi ní a celkovou energií funguje stejný vztah, jako mezi klidovou hmotností a klidovou energií. Tedy poměr mezi relativistickou hmotností a klidovou je stejný jako poměr mezi celkovou energií a klidovou. A relativistická hmotnost se musí brát v úvahu při výpočtu pohybu protonů v urychlovači. V daném případě se nám jako pozorovatelům, kteří jsou vůči urychlovači v klidu, budou jevit urychlené protony jako 3
Než se podíváme, jak to bude vypadat, když si přesedneme na některý z urychlených protonů, řekněme si, jaké jsou jejich rychlosti vůči velínu urychlovače. Ty lze spočítat z celkové energie částice a je rozumné je vyjádřit ve vztahu k velikosti rychlosti světla ve vakuu. Vůči pozorovateli sedícímu ve velínu urychlovače mají rychlost 0.999999964 rychlosti světla. Tedy rychlost protonů se liší od rychlosti světla jen o 3,6 miliontin procenta. Z našeho pohledu plyne čas na urychleném protonu 3
Podívejme se ještě, proč je výhodné využít srážku dvou vstřícných svazků oproti použití srážky urychlených protonů jednoho svazku s protony pevného terče. Pevný terč by mohl být výhodný. Má například daleko vyšší hustotu jader (třeba právě protonů), než je ve svazku. Připomenu, že v případě právě vodíku se označuje v našem slova smyslu jako pevný terč i terč vytvořený z kapalného vodíku. Tím by byl i větší počet srážek a z tohoto hlediska výhodnější situace. Mohli bychom urychlit proton na 7
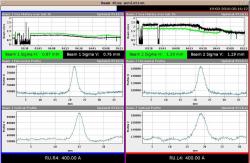
V případě urychlovače LHC srážíme dva protony se stejnými energiemi a tedy i hybnostmi. Nacházíme se tak v těžišťové soustavě systému těchto dvou protonů. Těžiště tohoto systému je vůči nám v klidu a s jeho pohybem není spojena žádná kinetická energie. Poměr mezi energií dostupnou při srážce vstřícných svazků a srážce svazku se stejnou energií protonů s pevným terčem roste s narůstající energií stále rychleji.
V citaci z diskuze zmíněné na počátku se objevil dotaz, jakou hmotnost protonu bychom pozorovali, jestliže budeme sedět na druhém protonu a určovat ji v okamžiku, kdy před srážkou letí ten první proti nám. Pro zjištění této hodnoty potřebujeme provést relativistickou transformaci rychlosti nebo energie. Pokud tyto transformace provedeme, zjistíme, že absolutní hodnota rychlosti proti nám letícího protonu se téměř neliší od jeho rychlosti pozorované z velína urychlovače, jen se ještě více přiblížila k rychlosti světla. Teď bude ještě více devítek za nulou, než se objeví první jiná číslice. Podstatně se však liší jeho energie. Jeho celková energie je nyní zhruba 26
Rozdíl hmotnosti protonu, který proti nám letí, a toho, na kterém sedíme, je dán podílem mezi uvedenou energií a klidovou energií protonu a tedy zhruba 27
Na Velkém hadronovém srážeči pátrají po tajemném kondenzátu barevného skla
Autor: Stanislav Mihulka (24.09.2019)
Jak se daří urychlovači LHC
Autor: Vladimír Wagner (11.11.2010)
Urychlovač LHC – rekapitulace a plány
Autor: Vladimír Wagner (01.01.2010)
Diskuze:
Co z toho vypadne
Adolf Balík,2010-03-31 20:44:11
To bude legrace zjistit, co z toho vlastně vypadlo. Když se z toho vyrazí moc energetické částice, tak ty vlastně v našem světě nemohou existovat, protože vstoupí vlastně do moc drsných interakcí s vakuem. Tyto interakce roztrhají ony částice i vakuum, ze kterého v jakési "ionizaci vakua" vyrvou jiné částice. Zbyde nám tedy jen sprška trosek obojího, jak produktů srážky tak roztrhaného vakua. Přijít na to, co bylo mezi srážkou a troskami následné kolize produktu z vakuem musí být docela oříšek, zvlášť kdyby přišlo něco zvlášť překvapivého, tudíž extrémně zajímavého.
Hawking
Milo Kubko,2010-03-31 01:10:42
2 Dalibor: Jedna se o Hawkingovo kvantové vyzařování černých děr, resp. quantum radiation. Nikterak extra jsem to nestudoval, ale pochopil jsem to zhruba tak, ze principy kvantove mechaniky (neustale chaoticky vznikaji a zanikaji pary castic) v blizkosti horizontu udalosti zpusobi, ze s nejakou velmi malou pravdepodobnosti se jedne z nich nebo zareni podari "vyskocit" ven.
Dalibor Frivaldsky,2010-03-31 11:31:10
tak je, aspon z toho co som vycucol z wikipedie. Jedna castica zo vzniknuteho paru castice-anticastice je pohltena ciernou dierou, druha unikne. Kedze vsak celkova energia musi byt zachovana ( energia pre vznik tohoto paru sa "splati" pri ich vzajomnej anihilacii kratko po vzniku ), tak tento energeticky deficit musi splatit cierna diera, cim strati energiu. Podla clanku u mikroskopickych ciernych dier by k tomu javu malo dochadzat vo vacsej miere. Celkom by ma zaujimalo, ak sa toto potvrdi, ktore castice z tychto parov su pohlcovane a ktore unikaju. Ci je to rovnomerne medzi casticou a anticasticou alebo niektora prevlada.
"Filosofická" interpretace Hawkingova zá
Vladimír Wagner,2010-03-31 12:16:25
Tento jev může mít i variantní interpretace oproti té, kterou uváděl Dalibor Frivaldský. První je například tunelování částic z míst pod horizontem do míst vně horizontu. Kvantová fyzika totiž neurčuje přesnou polohu částice, ale pouze funkci pravděpodobnosti jejího výskytu v různých bodech. Částice, která je těsně pod horizontem, má nenulovou pravděpodobnost výskytu vně horizontu. Další možná interpretace opět vychází z Heisenbergova principu neurčitosti. Díky němu může po krátký okamžik být hybnost větší než odpovídá zákonu zachování energie a hybnosti a tím pádem může být i rychlost částice nadsvětelná. Pokud se taková částice vyskytuje těsně pod horizontem, může tato rychlost stačit k jeho překonání. Tato nadsvětelná rychlost není díky Heisenbergově principu neurčitosti měřitelná, nenese informaci a neodporuje tak speciální teorii relativity. Ve všech třech variantách jde o čistě kvantové jevy a všechny zmíněné interpretace vedou ke stejným měřitelným důsledkům. Podrobnější populární povídání o kvantových vlastnostech "vakua" zde: http://hp.ujf.cas.cz/~wagner/popclan/vakuum/vakuum.html
On-line WebCam
Aronax Petr,2010-03-31 00:43:25
On-line WebCam - LHC
http://www.cyriak.co.uk/lhc/lhc-webcams.html
Ta snad zítra
Jan Kýla,2010-03-29 23:40:52
Tak snad zítra... Přeju nám všem hodně štěstí. A pokud nebude štěstí, tak aspoň dobrý výhled na ten ohňostroj. :-)
Jak je to s hmotností a rozměrem mikr. čer. díry
Vladimír Wagner,2010-03-29 22:04:43
Pro Martina Tůmu: V dáném případě se velká část kinetické energie srážejících se částic přemění na klidovou energii (hmotnost) mikroskopické černé díry. Tedy její hmotnost je dána velikostí dostupné kinetické energie(mnohonásobku hmotnosti protonu). Rozměr mikroskopické černé díry nemůže být pod Planckovou délkou. V tomto případě určuje energie vlnovou délku daného objektu. Pokud by měla být energie taková, aby aby vlnová délka byla kratší než Planckova délka (jen v tomto případě lze danou energii lokalizovat do daného rozměru), musela by být energie o mnoho řádů vyšší než energie dosažitelné na LHC. Proto na LHC nemohou vznikat klasické černé díry, pouze mikroskopické, které mohou existovat jen v případě, že na malé vzdálenosti (v řádu pod setiny poloměru protonu) platí jiný gravitační zákon a gravitační síla začne extrémně rychle růst. Více v tom odkazu, který jsem zde uváděl.
Hybnost mikroskopicke cerne diry
Martin Tůma,2010-03-29 20:25:12
To je zajimave, mel jsem za to, ze skoro vsechna energie srazky bude "pouzita" na vytvoreni cerne diry a ta samotna potom bude mit uz jenom malou hmotnost. Takhle do delky jejiho zivota pro pozorovatele v soustave velinu LHC vstupuje relativisticka dilatace casu, je fakt, ze rychlost jejiho vyparovani je tak mala, ze ani thle ji nezachrani. Nicmene jak rozmer diry, tak jeji predpokladany cas jsou pod Planckovou delkou a casem (pokud jsem se pri vypoctech neseknul s rady) - to uz je za hranici, kde funguji kvantova a gravitacni teorie. Ne ze bych jenom na okamzik predpokladal nejake problemy z teto strany, opravdu mne to zajima.
Mikroskopická černá díra
Vladimír Wagner,2010-03-29 16:14:58
Může vzniknout pouze mikroskopická černá díra (připomínám, že pouze hypoteticky). Ta je tisíckrát menší než proton, takže nepohltí ani celý jeden proton. A i dosah její gravitační interakce je takhle malý. Takže nemůže ovlivnit žádný další proton v srážejících se shlucích. Pro ní jsou skoro nekonečně daleko. Její rychlost bude většinou blízklá rychlosti světla (vzniká ve srážce částic s rychlostí světla). Blíže o tom zde: http://www.osel.cz/index.php?clanek=3703 . Mail je u této odpovědi nebo je lehce mě vygooglovat (domovská stránka i s mailem).
Jednalo se o odpověď Martinu Tůmovi
Vladimír Wagner,2010-03-29 16:29:59
Omlouvám se, zase jsem to neumístil v pořádku :-) Ještě malá oprava místo "vzniká při srážce částic s rychlostí světla" má být "vzniká při srážce částic téměř s rychlostí světla". Ke sdělovacím prostředkům. Také jsem si toho příspěvku na novinkách všiml. On už samotný text je dost tristní. I novinky už o LHC píší několik let. A zase je to úplně stejné "černá díra", "konec světa". Asi proto, že to je přesně to, co podle nich láká čtenáře. Uvažoval jsem tam v diskuzi přidat odkaz na vysvětlení právě třeba rozdílu mezi mikroskopickou černou dírou a klasickou černou dírou a proč nemůže klasická černá díra na LHC vzniknout nebo, proč díky existenci kosmického záření víme, že LHC Zemi neohrožuje, které jsem tu na Oslovi psal. Ale při pokusu o registraci mi odpověděli, že od 10.3. nové registrace do diskuze nepřijímají, takže to nešlo.
"vyparovanie" ciernych dier
Dalibor Frivaldsky,2010-03-29 22:13:42
A okrem jej zanedbatelnej velkosti, dochadza( ak si spravne pamatam ) podla pana Stephena Hawkinga ku uniku energie z ciernych dier. To znamna, ze to co cierna diera pohlti tam neostane navzdy, ale postupne vo forme energie ( predpokladam ze nejakej forme ziarenia ) z ciernej diery unika. Ak ma pan Hawking pravdu, dlzka exitencie tychto mikroskopickych ciernych dier by mala byt natolko mala, ze pred tym ako nieco stihnu pohltit sa uplne "vyparia"
Sdělovací prostředky
Lukáš Píše,2010-03-29 16:12:30
Sleduji články o urychlovači LHC na Oslu už nějáký čas i když tomuto tématu(částicová fyzika) nerozumím ani trošku ale zajímá mě pohled někoho kvalifikovaného.
Později narazím na článek ve sdělovacích prostředcích, které čte velká spousta lidí, zarazil mě už jen svým názvem.
http://www.novinky.cz/zahranicni/evropa/196063-v-obrim-urychlovaci-chystaji-simulaci-velkeho-tresku-pohlti-to-svet-varuji-kritici.html
Docela žasnu při pohledu na anketu:
Anketa
Obáváte se vzniku černé díry při experimentech v obřím urychlovači LHC? Celkem hlasovalo 32000 čtenářů. ano 54% ne 46%
Jako laikovy, který čerpal informace tady jsem si celkem jist že je to nesmysl a to jsem ještě spoustu věcí jistě nepochopil a ani jsem ještě nečerpal informace z jiných zdrojů....Kdo jsou ti jako že opůrci když čtu "Odpůrci experimentu se obávají vzniku černých děr, které pohltí svět."? Schovaly se někam...? Existují vůbec nějáké hodnověrné teorie jak by mohlo dojít k takovým věcem?...když pominu lechký popis scénářů na Oslu, který je vylučuje tak nemám nic co by do těchto pokusů (kromě poškození mašin) vnášelo nějákou nejistotu...
Celkova energie
Martin Tůma,2010-03-29 15:45:00
Dobry den, pane Wagnere. Rad bych Vas pozadal o Vas mail, rad bych Vas poprosil o malou konzultaci v oblasti kvantove fyziky, ktera se do zdejsich diskuzi nehodi. Zaroven bych se Vas rad zeptal, jestli pripadna cerna dira, ktera by pri techto srazkach mohla vzniknout, dokaze do sebe absorbovat energii celeho shluku protonu a druha vec - vzhledem k Vasem predpokladu nehybneho teziste - jakou maximalni rychlost pohybu by tento utvar mohl mit. Predem dekuji.
Pouhý atomový biliár
Adolf Balík,2010-03-29 10:29:19
Vyznavači politické korektnosti se těší, že zneužívání prostředků na politicky nekorektní buržoazní pavědu částicovou fyziku brzy skončí. Konkrétně tento urychlovač je prý pouhý atomový biliár. Vůbec to nepřispívá k Velké uhlíkové socialistické revoluci, a ta je přeci i prioritou Evropské komise. Co je věda se přeci určuje podle kritérií politické korektnosti a tato nauka se k ní nikdy nepřihlásila. Ohrožuje svatý boj proti globálnímu oteplování projektem Clouds a výzkumem závislosti tvrdého kosmického záření na podmínkách vysoké atmosféry. Proto se v grémiích určujících politickou korektnost diskutuje o ukončení vyhazování peněz za biliár a převedení těchto prostředků na účelnou a smysluplnou propagandu globálního oteplování:
http://motls.blogspot.com/2010/03/ian-lowe-use-lhc-money-for-agw.html
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce




