Když proud částic, například paprsek fotonů nebo elektronů, narazí na neprůchodnou folii s dvěma úzkými štěrbinami, procházejí jimi tak, že na stínidle kam dopadají, vytváří inferenční obrazec odpovídající pravidlům lomu a sčítání vln – difrakci a interferenci. K stejnému výsledku se dopracujeme, když namísto souvislého paprsku budeme ostřelovat otvory elektrony (fotony) postupně, jeden odděleně od druhého. I když tyto částice se nemůžou navzájem ovlivňovat a podle logiky našimi smysly vnímatelného světa prochází každá z nich buď jednou, nebo druhou štěrbinou, na stínidle dostaneme opět stejný interferenční obrazec jako u souvislého proudu elektronů. Je to absurdní, ale podle kvantové teorie každý elektron (foton) prochází oběma štěrbinami současně a chová se podobně jako rovinná vlna, která narazí na překážku se dvěma otvory. Ty se pak na druhé straně překážky jeví jako bodové zdroje a obě vlny, které se v nich tvoří, spolu interferují. To platí jenom do okamžiku, kdy se rozhodneme vystopovat kudy konkretně ten-který elektron (foton) prochází. Jeho chování se tím úplně změní. Bude jako hozený míček prolétat buď jednou, nebo druhou štěrbinou a žádné sčítání vln na stínítku neuvidíme ani po bilionté špehované částici. Pozorováním způsobujeme kolaps její vlnové funkce. (Fyzikální zákulisí dvojštěrbinového (Youngova) experimentu roztomile přibližuje video pod článkem. Průvodní slovo je v angličtině, ale animace je tak názorná, že při troše soustředění bude srozumitelná i beze slov.)
Interferenční obrazec u dvojštěrbinového experimentu je důsledkem Bornova pravidla, které definuje pravděpodobnost výskytu kvantového objektu na konkrétním místě a v konkrétním čase jako druhou mocninu jeho vlnové funkce (součtu jeho vlnových funkcí při dvou štěrbinách, kterými se „provlní“).
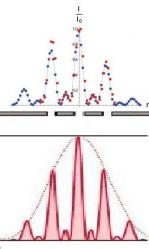
Při dostatečném množství částic (elektronů, fotonů) by u tříštěrbinového experimentu měl výsledný obrazec na stínidle odpovídat spodnímu třetímu grafu na obrázku vpravo. Jde o teoreticky vypočtenou křivku intensity záření, které prošlo třemi štěrbinami. Za nimi došlo k ohybu paprsků (k difrakci) a k jejich skládaní (interferenci).
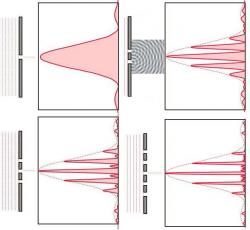
Obrázek vpravo: Když rovinná vlna (světlo z dostatečně vzdáleného zdroje) narazí na překážku s otvorem, ten se (díky ohybu světla) stane na druhé straně překážky bodovým zdrojem sekundárního vlnění. Když jsou otvory dva... tři... pět, dochází ke vzájemné interferenci vln z těchto jednotlivých zdrojů a jejich amplituda (u štěrbinových experimentů míra pravděpodobnosti dopadu částice na dané místo stínidla) má průběh odpovídající znázorněným teoretickým křivkám. Všimněte si, že všechny křivky se nacházejí ve stejné obálce (tečkovaná obalová křivka). Podle hyperphysics.

Dokázat experimentálně tento předpoklad se rozhodl rakousko – kanadský tým fyziků, kterému veleli Gregor Weihs z Universität Innsbruck za Rakušany a Urbasi Sinha z University of Waterloo za Kanaďany. Výzkum se uskutečnil v Ústavu pro kvantové výpočty University of Waterloo v kanadském Ontariu, kde vědci sestrojili technicky důmyslný systém. Měli k dispozici dva zdroje světla - pro vysílání jednotlivých fotonů (jako když střílí samopal) a laser s regulovatelným výkonem. Překážkou v cestě letícím fotonům byly dvě tenké kovové folie. V první, menší, byly tři stejné štěrbiny s rozměry 0,03 x 0,3 mm, vzdálené od sebe 0,1 mm. Druhá, stínící folie, měla vyřezané trochu větší otvory tak, aby mohly překrýt různé kombinace tří štěrbin menší destičky: všechny, nebo jenom některou, nějakou dvojici, nebo žádnou (obrázek vlevo). A samozřejmě koncovým článkem systému byl citlivý detektor, registrující ve vzdálenosti 18 cm od folie každý foton, kterému se jako vlně podařilo překonat štěrbinovou překážku.
Vědci provedli celou sérii experimentů se zdrojem „vystřelujícím“ fotony frekvencí 40 tisíc za sekundu na folii s otvory odkrytými v různých kombinacích (žádný, jeden, různé dvojice a všechny tři) a pak to samé s laserem vyzařujícím spojitý paprsek světla.
Výsledky nepovedou k přepisování učebnic, protože odpovídají teoretickým předpokladům. I nadále se tedy kvantová pravděpodobnost bude počítat podle pravidla, které formuloval v roce 1926 Max Born. V roce 1954 byl oceněn Nobelovou cenou a zde je jeho „nobelovská“ přednáška.
„Existence interferenčních vztahů třetího řádu by měla obrovské teoretické důsledky a zatřásla by jádrem celé kvantové mechaniky,“ vysvětluje Gregor Weihs. Podnětem pro celý pokus byla prý možnost, že kdyby se přece jenom podařilo zpochybnit základní pravidlo kvantové pravděpodobnosti, otevřelo by to tunel pro sjednocení dvou základních fyzikálních teorií – pro kvantovou mechaniku a gravitaci. Obě si zatím urputně chrání svojí nezávislost. „Náš experiment opět tuto snahu maří,“ dodává v koutku duše možná trochu zklamaný Weith. Zpochybnění by přineslo větší popularitu, než potvrzení.
Obrázek vpravo: Porovnání experimentálního výsledku s teoretickou křivkou. Horní obrázek znázorňuje výsledky tříštěrbinového experimentu pro souvislé světlo laseru (modré body) a „rychlopalbu“ jednotlivými fotony (červené body). Spodní křivka je deformace teoretické křivky tak, aby umístění štěrbin odpovídalo naměřeným maximám. Kredit: U. Sinha et al. Science 26. 7. 2010/ hyperphysics
Video vysvětlující dvojštěrbinový Youngův experiment:
Odborný článek o experimentu z roku 2008
Zdroje: Science 1, 2, photonics.com
Není teplota jako teplota a chladno jako chladno
Autor: Vladimír Wagner (03.01.2011)
Diskuze:
Prosim o dovysvetleni
Radim Doležílek,2017-10-26 19:36:50
Perfektni clanek a naprosto uzasne video. Vrta mi hlavnou jedna vec a byl bych rad, kdyby mi ji nekdo dovysvetlil. Ted jen doufam, ze spravne popisu na co se chci zeptat. Takze dve sterbiny a proud fotonu....v makrosvete normalne muzeme pozorovat interferenci svetla. Klasicky jev, klasicka fyzika. Ted teda prijdeme do mikrosveta a pri bombardovani tokem fotonu vznika taktez normalne pozorovatelna interference svetla na stinitku. Ted teda zacneme bombardovat jednolivyma fotonama. Takze nedochazi k interakci s jinou castici a foton by mel proletet jednou nebo druhou skvirou a neiteraktovat s nicim. Podle kvantove teorie vytvari superpozici a reaguje sam se sebou po pruchodu a k interferenci stejne dojde...proto je vysledkem interferencni obraz. Pokud se ale zacneme divat, tak dojde rozkladu vlnove delky a foton proleti jednou ci druhou skvirou (vytvari obraz dvou skvir na stinitku). Az doposud je mi to jasne a potvrzuje to kvantovou teorii. Prvni otazka: Kdyz teda budu bombardovat po atomu ale neskutecne rychle za sebou(tak abych to nemusel sledovat ze zaznamu kam dopadly ale primo).....tedy divam se, jsem tam, pozorovatel...uvidim interferenci nebo dve cary? (v makrosvete? v mikrosvete?) Cili v makrosvete, kdyz pozoruju normalni interferencni obraz na stinitku tak kvanotove zakony neplati? Svetelny tok se dale chova jako vlna...i kdyz to pozoruji?
Jirka Naxera,2010-07-30 23:52:06
Dekuji, po chvili googlovani jsem to nasel, celkem me potesilo ze jsem dospel k podobnemu nazoru jako tam napsani kritici kteri maji v oboru jmeno. :)
Opravdu si myslim (az bude cas tak to zkusim spocitat), ze ten konkretni experiment jde resit i bez kvantovky jenom vypoctem vln a jejich interferenci. To, ze vypnuti druheho zdroje rozostri obraz svedci jen o jedine veci - ze kolem tech dratku funguje difrakce a to, co vidime jako "jednu sterbinu" vubec neni jedna sterbina, ale nejaka interference toho z te "prave" + rozptyl o dratky + rozptyl z te neprave.
V jednom limitnim pripadu (zadna mrizka) to prejde do plne lokalizovane sterbiny a odstraneni mrizky nema zadny vliv (neni interference), druhy krajni pripad je, ze male sterbiny budou zarit plne podle interferencniho obrazce na nich bez zachovani smeru (neni lokalizace), ale nikdy nedojde k temto jevum soucasne.
zase omluva :(
Jirka Naxera,2010-07-30 23:55:48
Opet se omlouvam, zase vedle :( mela to byt reakce na http://en.wikipedia.org/wiki/Afshar_experiment
Jeste male upresneni/vysvetleni
Jirka Naxera,2010-07-31 00:11:36
Co jsem tim chtel rict: IMHO chyba Afsharovy interpretace je v tom, ze predpoklada ze kdyz nevidi obvykle interferencni obrazce, tak tam zadna interference neni. Naopak, to ze se obraz zostril je prave dukazem ze tam interference nastala, a vyrusila rozmazani (prispevek jedne sterbiny je priblizne v protifazi s tim z druhe, to plyne intuitivne z toho ze ty dratky samotne jsou v mistech interferencnich minim, kde opravdu oba paprsky musi byt v protifazi...).
Jako protiexperiment bych navrhl aby mely sterbiny ruzny tvar (treba jedna horizontalni druha vertikalni), pak by bylo snad na detektorech obstojne videt ze pres ty dratky opravdu nejde obraz jen jedne sterbiny.
Není to o tom, kolik člověk té fyzice dal,
Pavel Brož,2010-07-30 00:47:33
ono totiž tu nepochopitelnou věc, která se v populárně vědeckých publikacích odbude jenom nicneříkajícím klišé, že jde o projev korpuskulárně-vlnové duality, se snažily nějakou pochopitelnou formou vysvětlit jinačí kapacity, včetně nositelů Nobelových cen - a neúspěšně. Tak např. samotný zakladatel vlnové kvantové mechaniky, Schrödinger, zpočátku věřil, že vlnová funkce popisující elektron je "skutečná" hmotná vlna, podobně jako vlna v klasickém elektromagnetismu, tj. že to není jenom pravděpodobnostní vlna. Niels Bohr mu to na základě dalšího vývoje názorů na podstatu vlnové funkce a s použitím věrohodných argumentů později rozmluvil, což ovšem Schrödingera velice rozladilo, protože nové pravděpodobnostní pojetí kvantové teorie (ve kterém kvadrát vlnové funkce udával podle jiného fyzika, Maxe Borna, pouze hustotu pravděpodobnosti, viz zde diskutované Bornovo pravidlo) mu vůbec nebylo blízké.
Jiní fyzici, jako např. Charles de Broglie či David Bohm, sice akceptovali pravděpodobnostní interpretaci, nicméně elektron a jiné elementární částice chápali jakožto klasické hmotné body, které se pohybovaly po klasických naprosto deterministických drahách, které nám ale zůstávají neznámé v důsledku neznalosti tzv. skrytých parametrů, přičemž vlnová funkce určuje pouze pravděpodobnost nalezení částice, nestačí sama o sobě k určení kompletní dráhy částice.
Představa, kterou zmiňujete, má bohužel tu nevýhodu, že si neporadí s tím, když ten elektron rozdělíte pomocí dvou štěrbin vzdálených od sebe velice hodně (hypoteticky třeba několik světelných let daleko od sebe), a při průchodu tou jednou štěrbinou ho lokalizujete právě v té jedné štěrbině. Pokud by elektron byl opravdu dělitelnou hmotnou vlnou, jak navrhujete, tak co by se pak mělo stát s tím zbytkem té vlny? Mohl by se snad ten zbytek nadále autonomně pohybovat, a mohl by umožnit také detekci elektronu, ačkoliv ten už byl detekován? Bohužel nemohl, experimenty to vyvrací - ačkoliv je vlnová funkce dělitelná v tom smyslu, že ji můžete dělit do koherentních paprsků na různých štěrbinách, či v praktičtějších případech při průletu různými krystalickými materiály (prakticky se to ale činí s neutrony, nikoliv elektrony), tak po libovolném rozdělení jednočásticové vlny na paprsky libovolně daleko od sebe vzdálené lze detekci částice uskutečnit vždy jenom v jednom z dílčích paprsků.
To je opravdová záhada, a klišé o korpuskulárně vlnovém dualismu nic nezmění na tom, že to vážně záhada je. Kvantová teorie nám umožňuje počítat kvantové jevy a jejich pravděpodobnosti, ale neumožňují nám pochopit kvantovou teorii za pomocí analogií z klasické fyziky. To je prostě daná věc. My lidé žijeme ve škále, která nám umožňuje sbírat praktické zkušenosti pouze s klasickými jevy, a proto si stále chceme ten nepochopitelný korpuskulárně-vlnový dualismus vysvětlit pomocí klasických analogií, ale ono to prostě nejde.
Ono ale může jít docela dobře jenom o sílu zvyku. Tak třeba dnešní fyzici se podivují, jak vytrvale lpěli fyzici na přelomu devatenáctého a dvacátého století na představě éteru jakožto nezbytného média pro přenos elektromagnetických vln - ty se měly realizovat coby vibrace éteru analogicky, jako se realizuje zvuková vlna coby vibrace prostředí, jímž prochází. Dnes nám představa éteru přijde zbytečná a nemáme problém akceptovat elektromagnetickou vlnu i bez existence éteru.
Stejně tak možná za pár generací, až budou samozřejmostí kvantové počítače, a díky pokroku techniky až nebude žádný problém se od malička denně setkávat s projevy makroskopických kvantových jevů, tak se ty následné generace možná budou divit, cože nám přišlo tak nepochopitelného na kvantovém chování částic, na interferenci a jejím rušení v důsledku pozorování, na kolapsu vlnové funkce, na korpuskulárně-vlnovém dualismu. A budou se divit, proč jsme se tak urputně snažili všechny tyto věci připodobnit k naprosto neadekvátním jevům.
Jak to vidí primitiv jako jsem já.
Tomáš Janovský,2010-07-29 20:30:37
Elektron není kulička, ale shluk něčeho, co zatím neznáme a neumíme to změřit a ani popsat. Proto elektron jako celek projde jednou štěrbinou jako kulička. Ale pokud natazí na dvě a více štěrbin, rozpadne se jako když hodíte pitlík s vodou na plot, na druhé straně se potom jednotlivé části složí ale ovlivněné poměrem prošlích částí té každé díry a proto se zdá, že se chovají elektrony jako vlny.
Tak a teď se do mne pusťte. Z fyziky jsem měl za 4 a tak vim o tom veliké nic.
ohľadom experimentu
Martin Machava,2010-07-29 18:04:32
Mohol by som vás poprosiť o nejaké odkazy na tento experiment? Zaujímali by ma tiež parametre - aké široké boli štrbiny a ako vzdialené boli od seba.
Tiež aká je vlnová dĺžka elektrónu. Z čoho bol materiál, v ktorom sa tie štrbiny nachádzali?
Nemohlo pri bombardovaní toho materiálu dôjsť k tomu, že by elektróny naražajúce na okraj štrbiny zakrivili svoju trajektóriu za pomoci Coulombovej sily, alebo by "narazili" do elektrónu (vo valenčnej vrstve atómu, ktorý je umiestnený na okraji štrbiny) a ten "zvyšok" by sa oddelil a išiel už inou trajektóriou?
Dagmar Gregorova,2010-07-29 19:37:46
Veľkosť štrbín: zväčšte si tretí obrázok zhora (je naľavo od hlavného textu)
Pod článkom je odkaz na odbornú publikáciu z r. 2008. Je opisom v podstate identického experimentu.
Ešte predvčerom boli dostupné Supplementary Info k hlavnému článku v Science. Žiaľ, už prístupné nie sú. Ak máte naozaj záujem, môžem Vám to, čo som stiahla zo siete poslať na mail.
Také by vás mohlo zajímat..
Jiří Štros,2010-07-29 12:21:47
http://www.nature.com/news/2010/100728/full/news.2010.381.html
Opravdu to oko vidi sterbinu?
Jirka Naxera,2010-07-28 04:13:15
Tak v tom pripade si nejsem jisty, jestli pak vubec uvidime interferenci (z duvodu toho, ze fyzika je jina - v miste dopadu na sitnici se amplitudy scitat nemohou, uz proto ze obrazy obou sterbin jsou na jinych mistech sitnice), spis bych odhadoval, ze uvidime dve smouhy kolem obou sterbin.
Karel Š,2010-07-29 20:18:02
Pokud chcete znát podrobnosti najděte si popis toho experimentu, třeba na wikipedii. Samozřejmě kolem něj jsou jisté kontroverze ale z pohledu kvantové fyziky tam žádné problémy nejsou - ten foton stále "prolétává všemi možnými cestami" a to že detekujete že prošel jednou nebo druhou štěrbinou je jen důsledek kolapsu vlnové funkce, tedy náhodná veličina podobně jako je náhodná veličina to na který bod stínítka dopadne.
Dagmar Gregorova,2010-07-27 19:12:47
Dobře, prozatím - dokud vše nebude jasné, jsem všechny poznámky o interferenci pouze dvou možných drah pro jednotlivý foton zrušila. Je možné, že se vskutku jedná o (například) zavedení nových výrazů do rovnic s třetí mocninou a to je to, co Bornovo pravidlo vylučuje. Nevím, ale proč se i v článku píše, že multidráhová (více než 2) intereference je v rozporu s teorií. Přinutili jste mě se tématu i nadále věnovat :) a pokusit se ho doplnit o nezpochybnitelné vysvětlení. Na fyzikální stránce se píše: There are, however, no "third-order" terms involving waves travelling through all three slits. Napíšete i tam, že vlna se může podle Vás proplést všemi třemi štěrbinami?
Karel Š,2010-07-27 20:15:51
No tady už zase úřaduje angličtina - "There are no "third-order" terms involving waves travelling through all three slits" je tam míněno (aspoň podle mě) ve smyslu "[Even with three slits] there are just the known "second-order" terms (involving waves travelling through all three slits)". Takže proti téhle větě nelze nic namítat, jde ji ale pochopit různými způsoby. Ona je to celé tak trochu novinařina, jak jsem napsal na začátku vážně mi není jasné proč kolem toho dělají takový humbuk. To je jako kdyby v ústavu pro míry a váhy s velkou slávou odhalili že kilogram má opravdu tisíc gramů. Kdyby neměl, bylo by to jistě zajímavé. Ale takhle...?
Je to test Bornova pravidla
Pavel Brož,2010-07-28 00:21:44
Z toho abstraktu uvedeného pod číslem 2 u zdrojů plyne, že testovali, jestli Bornovo pravidlo, tak jak ho známe, platí. Bornovo pravidlo říká, jak se spočte měřitelná pravděpodobnost kvantově mechanických procesů z komplexní veličiny - vlnové funkce, obecněji pak z komplexních amplitud pravděpodobnosti. Tato komplexní vlnová funkce, resp. komplexní amplitudy, jsou přímo integrální součástí základního matematického aparátu kvantové teorie, který má sám o sobě svůj dobrý matematický smysl - konkrétně jde o prvky komplexních vektorových (přesněji Hilbertových) prostorů, velice často nekonečně rozměrných, a toto hřiště spolu se Schrödingerovou rovnicí, která udává časový vývoj vektoru z tohoto prostoru (vlnové funkce či amplitud pravděpodobnosti) zcela vystačí k tomu, aby byly matematici šťastní - i bez jakékoliv fyziky.
To, co ale spojuje tento panenský matematický ráj s reálnými četnostmi kvantových jevů, je právě Bornovo pravidlo - což je pravidlo, jak z oněch matematicky precizně spočtených komplexních veličin splácat nějakým brutálním způsobem reálnou veličinu - dokonce nejen reálnou, ale nezápornou veličinu, a to pravděpodobnost. Toto už není ta krásná esoterie nekonečně rozměrných komplexních prostorů, operátorů na nich působících, funkcionální analýzy atd. - to už je přízemní fyzikální požadavek. Tento požadavek naplnil Born svým postulátem, že pravděpodobnost se vypočte z komplexních amplitud jakožto kvadrát jejich absolutní hodnoty. Klasik ze známé české komedie by to glosoval jakožto "primitivní, ale účinné". Přesně tak to funguje, v Bornově pravidle není ukryta žádná hlubší filosofie, která by odůvodňovala, že má vypadat zrovna tak, jak jej Born postuloval. Bornovo pravidlo je prostě naprosto nezávislý postulát, který dolepen ke krásné matematice Hilbertových prostorů působí jako Mercedes s koly od Velorexu.
Na téma pokusů, jak v kvantové teorii nějak "odvodit" Bornovo pravidlo z nějakých elegantnějších či sofistikovanějších matematických předpokladů, byly popsány stohy článků - žádný z nich žádné přesvědčivé odvození nepřinesl. Proto Bornovo pravidlo i nadále provokuje, podobně, jako svého času provokoval geometry pátý Euklidův postulát. V uvedeném článku se evidentně pokusili experimentálně ověřit, zda by neexistovala nějaká evidence pro zobecnění tohoto pravidla, kde by patrně hrály roli i vyšší mocniny amplitud pravděpodobnosti, než druhé - a výsledek testu to zřejmě moc neprokázal.
Mimochodem, vícero teorií počítá s tím, že Bornovo pravidlo může být modifikováno o tyto vyšší mocniny. Příslušné modifikace jsou samozřejmě zaváděny s ohledem na minulé experimenty, tj. natolik malé, aby nebyly v protikladu s minulými experimenty (samozřejmě, nevymýšlíte přece novou teorii tak, aby byla neplatná už při svém zrodu). Tzn. že výsledek tohoto experimentu samozřejmě není žádným definitivním potvrzením, že Bornovo pravidlo, tak jak se vyskytuje v učebnicích kvantové teorie, je jediné možné. Výsledek tohoto experimentu pouze mohl vyloučit některá z těchto zobecnění a na ta ostatní naklást přísnější limity.
Vzorecek
Tomáš Brauner,2010-07-28 09:21:01
Nekdo tady volal po vzorecku, tak ho jen strucne doplnim. Mozna to osvetli, v cem spociva ta "interference tretiho radu", i kdyz vetsine diskutujicich uz je to asi jasne. Oznacime-li fA,fB,fC (komplexni) amplitudy pravdepodobnosti, ze foton prosel sterbinami A,B,C, pak zakladni pravidla kvantove mechaniky rikaji zhruba, ze pokud nedokazeme rozlisit, kterou sterbinou foton proletel, je jeho kvantovy stav na stinitku popsan souctem f=fA+fB+fC. V tomto souctu je skryty fakt, ze foton "proleta vsemi sterbinami soucasne". Pravdepodobnost dopadu na urcite misto stinitka pak bude dle Bornova pravidla dana kvadratem
|f|^2 = |fA|^2 + |fB|^2 + |fC|^2 + fA fB* + fA* fB + fA fC* + fA* fC + fB fC* + fB* fC.
(Hvezdickou znacim komplexni sdruzeni.) Protoze pocitame kvadrat vlnove funkce, budou interferencni cleny obsahovat vzdy soucin pouze dvou amplitud. To je ta absence "interference tretiho radu". Stale ale foton proleta vsemi sterbinami soucasne, coz je ostatne videt i z obrazku u clanku, nebot zmereny interferencni obrazec odpovidajici pruletu jednotlivych fotonu je stejny jako pro "spojite" zarici laser. Kazdy jednotlivy foton se tedy chova jako rovinna vlna.
Kdyby skutecne interferovaly jen dve mozne drahy, napriklad A a B (coz lze zaridit tak, ze budeme sledovat sterbinu C, zda ji foton neproletel), byla by vysledna pravdepodobnost dana vztahem |fA + fB|^2 + |fC|^2 a vysledek by byl pochopitelne jiny.
Takze ten experiment skutecne primo testuje, zda kvantova pravdepodobnost je dana kvadratem vlnove funkce a neobsahuje nahodou nejake cleny vyssiho radu. Souhlasim ovsem s Karlem S, ze se kolem toho experimentu dela prilisny humbuk. Anebo spis jde (jako v jinych pripadech) o sikovny marketing autoru. Ve skutecnosti je totiz Bornovo pravidlo zakladem, z nehoz vychazi vypocet jakekoli pozorovatelne veliciny v kvantove mechanice. Takze jeho testem - trebaze neprimym - je KAZDY experiment, jehoz interpretace se opira o kvantovou teorii. Spis by tedy bylo zajimave navrhnout experiment, ktery by Bornovo pravidlo dokazal overit s pokud mozno co nejvyssi presnosti. Takoveto prime mereni urcite nebude tou spravnou cestou a ma tedy spis jen pedagogicky vyznam.
Video ..
Antonín Holík,2010-07-27 18:26:31
Tak jsem si jeste pustil to video .. to je z 'what the bleep' ! Dobry ..
Karel Š,2010-07-27 20:10:29
To video je krásné, ale nepřesné. Ve skutečnosti je možné sledovat kterou štěrbinou foton prošel a interferenční obrazec nenarušit - nejsnáz tak že si nestoupnete ke štěrbině ale před stínítko, pokud vám pak foton přiletí do oka tak vidíte ze které štěrbiny to bylo. Skutečně už byly provedené příslušné experimenty a ty fungovaly, jeden z nejznámějších je Afshar(ův) experiment.
Pokud se chcete s problematikou seznámit hlouběji, vřele doporučuji sérii přednášek ze Stanford University o entanglementu (vyhledejte na youtube "Lecture 1 | Quantum Entanglements, Part 1 (Stanford)"), jsou velmi dlouhé ale podané tak aby to měl šanci pochopit i naprostý laik a opravdu vysvětlují o co tam jde.
Video zkresluje pojem pozorovatele
Bronte Harkaitz,2010-08-03 14:36:55
Problém je, že interpretace "What the bleep..." jsou neskutečně zkreslené a hozeny do magie new age.
Jim nešlo v principu o popularizaci vědeckého poznání, ale právě o propagaci jakéhosi newagescientismu. Pokud chce člověk populár tak sáhne k dokumentům od BBC.
Popis v ukázce od Dr.Quantum je moc pěkný a velmi výstižný - v podstatě jediný světlý moment v nesmyslu "What the..."
Ale i zde je vidět ona magie - Děda mluví o tom jak se chování částic změnilo tím, že ho vědci pozorovali. Interpretace naznačuje, že jde o interakci s vědomou myslí a to je samozřejmě zcela chybné. Jde o interakci tím, že se něco měří a tím se to pozmění - může to dělat i počítač. Naprosto nezávisí, že pozorovatel je Richard Feynman nebo moje kalkulačka, jde jednoduše o interakce hmoty a magie ohledně mysli sem zcela nepatří.
OK, pak prosim o vysvětlení - DĚKUJI
Dagmar Gregorova,2010-07-27 13:18:06
Fakt nemám vystudovanou teoretickou fyziku, takže PROSíM o vysvětlení následujících informací - poslední je z abstraktu článku (zejména by mě zajímalo vysvětlení odborně erudovaného pana Holíka):
In the case of three slits, the calculation produces three terms describing interference between waves travelling through the three possible pairs of slits. There are, however, no "third-order" terms involving waves travelling through all three slits.
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Born’s rule is one of the key laws in quantum mechanics, and it proposes that interference occurs in pairs of possibilities. Interferences of higher order are ruled out.
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Born’s rule predicts that quantum interference, as shown by a double-slit diffraction experiment, occurs from pairs of paths. A generalized version of quantum mechanics might allow multipath (i.e., higher-order) interference, thus leading to a deviation from the theory.
Antonín Holík,2010-07-27 16:59:30
V pripade tri sterbin se vypocet sklada ze tri clenu popisujicich interferenci mezi vlnami prochazejicimi skrze tri mozne pary sterbin. Neni zde ale zadny clen obsahujici vlny prochezejici skrz vsechny tri sterbiny.
Coz ovsem je diskutabilni. Protoze pokud se to vse sklada z takovych clenu, tak celek je sam clenem ktery obsahuje vsechny sterbiny. Vubec neni jasne co tim chteli rict, obavam se.
Vzorce samotne by mozna byly jasnejsi.
Karel Š,2010-07-27 17:29:38
Když si nalistujete Born's Rule na wikipedii zjistíte že se žádnými páry neoperuje. To je jen obecný mechanismus jak se kvantový stav převádí na "observable", což je laicky řečeno výsledný interferenční obrazec. Interferenční obrazec u dvou štěrbin vzniká proto, že se skládá kvantový stav, ne výsledné obrazy na stínítku a výsledný obraz je tedy zobrazením nové kvantové funkce vzniklé složením těch původních. "second order" tady znamená že tady existuje kvantový stav a výsledek na stínítku je jen jeho projekcí. To že neexistuje "third order" jen říká že třetí štěrbina do toho nevnese žádnou novou kvalitu a že si tedy vystačíme se stávajícím modelem kvantového stavu, stávající metodou jejich skládání a projekce.
Antonín Holík,2010-07-27 13:02:07
Nojo .. to neni poprve co je odborny clanek prelozen trochu neodborne ..
Dagmar Gregorova,2010-07-27 14:14:44
Mohli by jste prosím konkretizovat, který článek je "přeložen" a jaké jiné neodborně přeložené články máte na mysli? Kdybyste tušil, z kolika zdrojů je to uplácané... ale proč bychom si nekopli, že? A čím jste chtěl přispět do diskuze?
Antonín Holík,2010-07-27 16:44:05
To mela byt poznamka k prispevku Karla S. Pisete ze foton proleta dvema sterbinama, coz proste neni pravda.
Dagmar Gregorova,2010-07-27 17:03:32
...a jak tedy mám rozumět informacím uvedeným v nejvrchnějším diskusním příspěvku? Možná se mýlím, ale já je chápu tak, jak jsem to napsala v článku - a věřte, že jsem se nad tím dost zamýšlela - také jsem si myslela, že se foton chová jako rovinná vlna a tedy přechází všemi štěrbinami. Právě to, co jsem si přečetla, mě přesvědčilo, že tak asi není.
Diskusní příspěvek může být na oslu dost dlouhý na to, aby jste všem, nejen mně, poskytl srozumitelné vysvětlení. Nebo napsal krátký článek, který uveřejníme. Já totiž pořád chápu smysl pokusu v potvrzení/vyvrácení předpokladu, že existuje jenom interference mezi páry možných drah a ne mezi trojicemi.
Opakuji, připouštím, že se mýlím. Pak ale musím článek opravit, ale na to potřebuji vysvětlení, které by mě vyvedlo z omylu. Dopředu děkuji.
Foton samozřejmě prolétá všemi třemi...
Karel Š,2010-07-27 12:40:02
... a kromě toho letí ještě všemi ostatními možnými cestami jako úplně kolem překážky nebo dvakrát kolem zeměkoule a výsledný obrazec je součet všech těchhle cest, to je základ kvantové mechaniky.
Tady nejde o to že foton letí dvěma štěrbinami a tou třetí ne. Tady jde o to, že výsledek pokusu se dvěma štěrbinami se nedá popsat jako kombinace výsledků pokusu s jednou štěrbinou, zatímco tři štěrbiny (a více) už lze popsat jako kombinace výsledků pokusů se dvěma. Což je sice důležité, ale trochu mě udivuje ta sláva kolem toho. Každá difrakční mřížka je pokus s desítkami až tisíci štěrbin a kdyby tam bylo něco co odporuje teorii, myslím že by se na to už dávno přišlo...
Jsme holt borci.
Bronte Harkaitz,2010-07-27 10:57:14
Velice zajímavé. A co k té změně hmotnosti protonu? Těšil jsem se na skandální otřes a ono zatím nic :-)
Dagmar Gregorova,2010-07-27 11:57:42
;)
Také jsem si s potěšením přečetla zprávu o menším protonu a když jsem si uvědomila, že kolik jich tvoří mé „já“, okamžitě jsem si zkusila starší oblečení – to přece se musí projevit!
:( Hmmmm… tak nevím, asi se nezmenšily… :)
Ale vážně - kdybyste věděl, kolik je témat na psaní... Kdyby měl V. Wagner na nás více času a "neflákal" se :) po všelijakých experimentech rozbíjejících nejen atomy, ale i ty jejich drobné trosky! (A to fyzikové chtějí ještě výkonnější urychlovač! )
Menší proton neznamená menší atom, chtělo by to „dohledat“, co z těch – 4 procent vyplývá a nakolik se liší od možné chyby v současnosti dostupných měření. Nemám ráda informační "BOMBY".
Ale jsou i jiná „šokující“ :) témata: Například před asi 2 měsíci obíhala bombastická zpráva, že Fermilab objevil zvláštní typ nesymetrie mezi hmotou a antihmotou (Při rozpadu mezonů B0 dochází k jednoprocentnímu rozdílu mezi počtem vznikajících párů mionů a párů antimionů). A pak se objevila již nikým nepovšimnutá zpráva, že to jiný experiment vůbec nepotvrdil a jemu rozpad vyšel symetrický...
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce