Od března 2020 mají detekční systémy LIGO a VIRGO přestávku, která byla způsobena i epidemií COVID-19. Během ní se pracuje na vylepšení zařízení i metodiky jejich pozorování. Intenzivně se však pracuje také na analýze dat, která se získala v předchozím období jejich činnosti. Připomeňme, že zatím proběhly tři periody měření.
První se realizovala v období od 12. září 2015 do 19. ledna 2016 a podařilo se v ní zachytit tři případy splynutí černých děr. První zachycení gravitačních vln z takového jevu nastalo již 14. září 2015. Publikováno bylo v únoru 2016. Další případy pak následovaly.
Druhé období experimentování proběhlo mezi 30. listopadem 2016 a 25. srpnem 2017 Během něj se podařilo zachytit a identifikovat gravitační vlny ze sedmi případů splynutí černých děr a první případ splynutí neutronových hvězd. Ten byl velice blízký a byl zachycen i jako krátký záblesk gama, i v dalších oblastech elektromagnetického spektra. To umožnilo potvrdit předpokládanou souvislost mezi krátkými záblesky gama a splynutími neutronových hvězd i srovnat rychlost gravitačních vln s rychlostí světla.
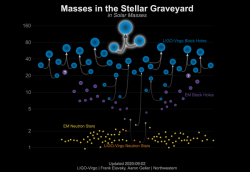
První dvě období experimentování tak umožnila získat první statistiku případů. Zjistilo se, že černé díry pozorované pomocí gravitačních vln mají mnohem větší hmotnost, než mají ty, které pozorujeme v binárních systémech v naši blízkosti. To je ale vysvětlitelné výběrovým efektem. Binární systémy jsou pozorovatelné a identifikovatelné našimi přístroji jen do určité omezené vzdálenosti. Protože je velmi hmotných černých děr o mnoho řádů méně než těch s nízkou hmotností, je pravděpodobnost, že by byly v blízkém okolí, velmi malá. Výskyt binárních černých děr a jejich splynutí je velice málo pravděpodobný jev a musíme pozorovat hodně velký objem prostoru, abychom je mohli zaznamenat. A ve velké vzdálenosti uvidíme jen splynutí černých děr s velkými hmotnostmi, které vyprodukují dostatečně intenzivní impuls gravitačních vln.
Třetí období detekce pak proběhlo od 1. dubna 2019 do 27. března 2020. Zatím se analýzou získaných dat podařilo identifikovat dvě splynutí černých děr, další splynutí dvou neutronových hvězd a případ splynutí černé díry s kompaktním objektem s relativně malou hmotností. A právě při jednom ze zachycení gravitačních vln, které proběhla 21. května 2019, došlo k pozorování gravitačních vln se splynutí zatím nejtěžších pozorovaných černých děr. Výsledky analýzy tohoto případu byly publikovány právě v těchto dnech. Je třeba ještě poznamenat, že ve všech třech popsaných obdobích pozorování byla kromě popsaných spolehlivě prokázaných případů zaznamenána i řada kandidátů a signálů, které byly blízko úrovně šumu.
Různé typy černých děr
Zatím se nám přímo podařilo pozorovat pouze dva typy černých děr. Prvním jsou hvězdné černé díry, které jsou konečnými stádii velmi hmotných hvězd. Jejich hmotnost je omezena na desítky hmotnosti Slunce. V principu mohou existovat hvězdy s hmotností svého jádra vyšší, ovšem před svým koncem se stávají velmi nestabilní a jejich jádro nekončí v černé díře. Existuje tak limita na možnou konečnou hmotnost hvězdného jádra, která omezuje i hmotnost hvězdné černé díry. Ta vede podle současných modelů k omezení hodnoty pro hvězdné černé díry okolo 65 hmotností Slunce.

Nepřímo jsou černé díry hvězdného typu pozorovány ve dvojhvězdách prostřednictvím rentgenovského záření a odhadu hmotnosti kompaktního objektu, který přesahuje limitu na hmotnost neutronové hvězdy. Přímo jsou pak pozorovány právě pomocí detekce gravitačních vln vyzářených při jejich splynutí.
Druhým známým typem jsou supermasivní černé díry v jádrech galaxií. Jejich hmotnosti jsou mezi statisíci až desítkami milionů hmotností Slunce. Nepřímo je lze pozorovat pomocí jejich gravitačního vlivu na blízké hvězdy nebo pomocí vysokoenergetických procesů, které způsobují v aktivních jádrech galaxií a kvasarů. Přímo pak byla tato supermasivní černá díra pozorována radioteleskopem v galaxii M87.
Předpovídá se však i existence středně hmotných černých děr, jejichž hmotnosti by byly mezi horní limitou pro hvězdné černé díry až tisíci hmotností Slunce. Jejich existence zatím prokázána nebyla. Existují sice náznaky, že by se mohly vyskytovat ve středu některých kulových hvězdokup, ale zatím nepříliš průkazné. A právě zmíněný případ zachycení gravitačních vln GW190521, který se uskutečnil 21. května 2019 by mohl být prvním případem pozorování takových černých děr. Ještě je třeba poznamenat, že by mohly existovat extrémně hmotné hvězdy, jejichž jádro má hmotnost přesahující 135 hmotností Slunce. Ty se vyhnou popisované nestabilitě a jejich jádro pak zkolabuje přímo do středně hmotné černé díry.
Detekce gravitačních vln GW190521
Stejně jako u ostatních pozorování splynutí černých děr trval záblesk gravitačních vln velmi krátce. Oproti těm předchozím však byl ještě mnohem kratší, trval méně než desetinu sekundy. I to indikovalo, že jde o splynutí černých děr s velmi vysokou hmotností. Analýzou signálů se ukázalo, že šlo o černé díry s hmotností 85 a 66 hmotností Slunce, které splynutím vytvořily černou díru o hmotnosti142 hmotností Slunce. Okolo 9 hmotností Slunce se vyzářilo právě v podobě gravitačních vln. Pochopitelně, že jsou tyto hodnoty hmotností zjištěny s jistou nejistotou. První hmotnost však určitě překračují hodnotu možnou pro hvězdnou černou díru a je nižší, než by vznikla přímým kolapsem do středně hmotné černé díry. Tato složka tak musela vzniknout předchozím splynutím méně hmotných černých děr. K události došlo ve vzdálenosti přesahující 10 miliard světelných let, tedy blízko samého okraje pozorovaného vesmíru
Toto pozorování se může stát zlomovým. Zatím nevíme, jak vznikají supermasivní černé díry v jádrech galaxií. Může jít o proces, při kterém postupně splývají hvězdné černé díry a posléze i středně hmotné černé díry. Takový jev může nastávat jen v prostředí, kde je vysoká hustota černých děr. Je tak pravděpodobné, že i námi pozorovaný případ proběhl v nitru nějaké kulové hvězdokupy, kde je vysoká hustota hvězd a následně černých děr. Zároveň pak musí existovat různá stádia jejich vytváření, tedy černé díry s hmotností mezi hmotností hvězdných černých děr a supermasivních černých děr. Jinou možností je zatím neznámý proces, který vede k okamžitému vzniku zárodku supermasivní černé díry.
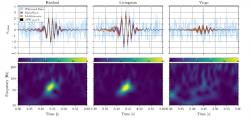
První pozorování splynutí černých děr, které mají větší hmotnost než hvězdné černé díry, je velmi důležitým krokem k vyřešení otázky vzniku supermasivních černých děr. Je velká naděje, že budoucí pozorování pomohou vyřešit záhadu vzniku středně hmotných i supermasivních černých děr. Podrobný rozbor tohoto pozorování byl publikován ve dvou článcích (zde a zde).
Hon na další takové události
Pravděpodobnost takové události, jako je splynutí černých děr s velkou hmotností je velmi malá. Proto je třeba je pozorovat do co největší vzdálenosti. Potřebujeme tak co nejvyšší citlivost detekce. Právě zlepšení citlivosti je cílem vylepšování, které probíhá během přerušení pozorování způsobené koronavirovou pandemií. Vylepšovat se budou i analyzační metody pro detekci a identifikaci co nejkratších signálů. Ty by měly přicházet právě od těch velmi masivních černých děr. Je tak vysoká šance, že se po obnovení pozorování dočkáme brzy dalších velmi zajímavých případů pozorování velmi masivních černých děr.
Závěr
Na závěr je třeba ještě zmínit, že interpretace detekce gravitačních vln GW190521 pomocí splynutí velmi hmotných černých děr je tou nejpravděpodobnější. Ovšem vysvětlit ji mohou i jiné mnohem exotičtější hypotézy, ve kterých mohou vystupovat i tak exotické objekty, jako jsou kosmické primordiální struny, které jsou pozůstatkem inflačního období našeho vesmíru.
Interpretace není úplně jistá ani u zatím posledního identifikovaného případu GW190814. V tomto případě šlo o splynutí černé díry s hmotností 23,2 hmotností Slunce a kompaktního objektu s hmotností pouhých 2,6 hmotností Slunce. Druhý objekt tak má hmotnost, která je v intervalu přechodu mezi jasnými hmotnostmi neutronové hvězdy a černé díry. Jde tedy o velmi zajímavou kombinaci, která je dalším příkladem nového typu případů. Podrobnější rozbor tohoto případu byl publikován zde.
Lze očekávat, že vylepšená zařízení LIGO a VIRGO v dalším období experimentování přidají další zajímavé případy a posunou naše znalosti vývoje vesmíru. Ty by mohly pomoci vyřešit řadu otevřených otázek spojených se současným kosmologickým modelem, viz přednáška:
Diskuze:
Trvání gravitačního záblesku
Zdeněk Mařík,2020-09-05 23:56:56
Dobrý den a díky za článek!
Jen mě překvapuje ta krátká doba záblesku/vlnění gravitačních vln. Jak jsem zatím všude četl, předpokládá se (především u dvojhvězd) poměrně šílená rychlost vzájemné rotace/oběhu než dojde ke kontaktu. Zmíněné ČD musely mít velmi orientačně Schwarzschildův poloměr cca 255 a 198 km (platí-li Rs =~3M). Jestli to byla původně dvojhvězda, pak kolem sebe musely rotovat poměrně dlouho, než došlo ke kontaktu horizontů událostí a vlnění prostoru muselo být již v té době veliké.
Ve kterém okamžiku předpokládá současná teorie, že dochází k onomu detekovanému záblesku gravitačních vln? Když se dotknou horizonty událostí nebo průběžně od kontaktu po dobu splynutí? Pokud by šlo o dobu splynutí horizontů událostí, znamenalo by to, že vše bylo vyřízeno na 0.1s (bez ohledu na to, co a jak dlouho se následně děje pod "novým" horizontem)?? Tj. za 0.1s vytvořen nový horizont událostí a vyzářeno 9M v podobě gravitačních vln??
Děkuji za odpověď.
Re: Trvání gravitačního záblesku
Pavel Brož,2020-09-06 15:33:49
Dobrý den, tam není žádný přesně definovatelný okamžik, během kterého dojde k tomu záblesku. Celý proces je spojitý, gravitační vlny jsou vyzařovány už milióny let před splynutím, díky tomu se k sobě ty černé díry přibližují, tím ještě více zesílí to vyzařování gravitačních vln, atd., až ve výsledku dojde ke splynutí horizontů. Ani během něj toho splynutí horizontů se co se týče vyzařování těch vln neděje kvalitativně nic jiného, než co se dělo celé ty milióny let předtím, pouze v jistém okamžiku nastane maximum to rozvlnění okolního prostoru, přičemž pro nás je to rozvlnění pozorovatelné pouze pár zlomků sekundy kolem toho maxima.
Ty horizonty událostí se ještě před tím splynutím deformují, a nakonec se spojitě slijí v jeden. V pár komentářích níže zazněla představa, že se na sebe budou ty černé díry svými horizonty lepit jako polystyrénové kuličky - není tomu tak, ten horizont událostí není žádná "skutečná" hranice, je to opravdu jenom horizont, tj. přeneseně nejzazší místo, kam až nekonečně vzdálený pozorovatel při pohledu směrem k černé díře "dohlédne", více přesněji řečeno kam až může zmapovat děje v okolí černé díry při použití svého souřadného systému. V určité vzdálenosti od středu černé díry mu vznikne souřadnicová singularita, a tu nazýváme horizontem událostí.
Pokud by ale ten pozorovatel padal do těch slévajících se černých děr, tak pokud by to byly opravdu gigantické černé díry, nepozoroval by nic zvláštního. Nejhmotnější gigantické černé díry nacházející se v jádrech velkých galaxií mají hmotnost přes deset miliard Sluncí, viz seznam zde https://en.wikipedia.org/wiki/List_of_most_massive_black_holes . Pozorovatel padající skrze horizont by zakoušel pouze slapové síly, protože gravitační zrychlení by se ve shodě s principem ekvivalence eliminovalo jeho volným pádem. Velikost slapové síly na horizontu by v případě černé díry o hmotnosti deseti miliard Sluncí a v případě dvoumetrového člověka padajícího nohama napřed byla několik stomiliardtin g, tedy naprosto zanedbatelná. I v případě pádu do slévajících se dvou takovýchto gigantických černých děr by ten padající pozorovatel nic zvláštního nezaznamenal, žádný horizont by během svého pádu nepotkal, akorát by nakonec bídně zhynul ve středu výsledné černé díry (pokud by měla hmotnost těch deset miliard Sluncí, padal by do jejího středu asi den a půl – pokud bychom to počítali bez zakřivení prostoru pod horizontem, vyšlo by nám že by padal jenom asi den, ale v důsledku toho zakřivení se délka té cesty do centra černé díry o něco prodlouží). Prostě lokální pozorovatel by žádný dotyk horizontů nezaznamenal, bez ohledu na to, jak by si načasoval svůj pád dovnitř, jestli by spadl pod horizont před slitím, nebo po něm, nebo přesně v okamžiku slití, prostě by žádný horizont neviděl. Teď se samozřejmě nebavíme o kvantových jevech, kde dodnes panuje nejednotnost názorů, jaké konkrétní kvantové jevy na horizontu mají z pohledu padajícího pozorovatele vznikat, jedni tvrdí, že tam bude zažívat ohnivé inferno, druzí tvrdí, že nic takového nezaznamená – každopádně tato otázka nijak nesouvisí s intenzitou odnášených gravitačních vln.
Takže ono to splynutí horizontů je jenom něco, co může definovat velmi vzdálený pozorovatel čistě jen v důsledku toho, že jeho souřadnice při popisu oblastí příliš blízkých středům těch černých děr selhávají. Pro lokálního pozorovatele sledujícího celou tu událost z první ruky přímo na místě – a v případě slévání gigantických černých děr by se mu přitom nic zvláštního nedělo, protože slapové síly by byly zanedbatelně malé – by se tam nikde nic neslévalo, protože by z jeho pohledu nebylo co by se mělo slévat. To rozvlnění okolního prostoru si můžeme zhruba připodobnit jako vlnění vodní hladiny při slévání dvou kolem sebe rotujících vodních vírů, ani tam nenajdeme nějaký konkrétní okamžik, který bychom přisoudili maximu těch vln, i když z logiky věci je samozřejmě jasné, že to maximum nastane někdy kolem toho splynutí.
Re: Re: Trvání gravitačního záblesku
Vladimír Wagner,2020-09-06 15:48:29
Díky Pavle za perfektní doplnění a vysvětlení i v dalších částech diskuze. Myslím, že to spoustě čtenářů pomůže v pochopení této problematiky. I pro mě je to velice inspirativní v tom, jak se to dá velice dobře a srozumitelně vysvětlit. Díky Tvým příspěvkům si spoustu věcí ujasním.
Re: Re: Re: Trvání gravitačního záblesku
Pavel Brož,2020-09-06 23:54:33
Není zač děkovat, diskuze tu jsou od toho, aby se téma co nejvíce vyložilo čtenářům, i s jejich pomocí :-)
Re: Re: Re: Re: Trvání gravitačního záblesku
Zita Šustová,2020-09-09 10:32:24
Zeptám se Vás pane Broži : jaký materiál je v ČD ?, jaký druh hmoty tam je ? jaké částice ? aby to dávalo pak hmotnost 30 Sluncí..., mají ty částice náboje ?, v jakém ne-plazmatickém stavu tam je ta hmota ? Díky. Pak se zeptám na druhou otázku : zda všechny ČD mají stejné "složení" hmoty, stejný druh částic a tedy když splynou zda jak vadí/nevadí různost hmoty těch dvou, aby vydaky gravitační vlny. Díky.
Re: Re: Re: Re: Re: Trvání gravitačního záblesku
Vladimír Wagner,2020-09-09 11:36:32
I když je dotaz směřovaný na Pavla Brože, pokusím se odpovědět já. Co je pod horizontem černé díry můžeme na jedné straně říci a na druhé straně ne. Závisí to na tom, v které části pod horizontem černé díry je a jaká je to černá díra. Takže bych se to snažil vysvětlit v několika bodech:
1) Pokud se objekt (částice) dostane pod horizont černé díry, už se nemůže z pod něj dostat (musel by dosáhnout rychlosti světla) a nezadržitelně padá do středu černé díry.
2) V jakém je stavu, závisí (jak už se v diskuzi psalo) na gradientu gravitačního pole v místě horizontu. Tedy pro supermasivní černou díru v centru galaxie by měl být gradient malý a objekt by neměl nic pozorovat (odhlédněme nyní od hledání kvantové teorie gravitace a kvantové jevy hypoteticky s ní spojené a popisující horizont) a bude mít tedy normální složení. U hvězdné černé díry toto neplatí, gradient gravitačního pole je velký a složení hmoty bude dáno tlaky a teplotami, které jsou vytvářeny právě tímto gradientem gravitačního potenciálu a hromaděnou hmotou v daném místě. U supermasivních černých děr je to hlouběji pod horizontem blíže jejímu nitru. Takže s růstem tlaku dostaneme postupně plazma (jako ve hvězdách), degenerovaný elektronový plyn (jako v bílých trpaslících) a neutronovou kapalinu či dokonce kvark-gluonové plazma (jako v neutronových hvězdách). Protože současná fyzika a standardní model hmoty a interakcí neobsahuje hmotu, která dokáže odolat tlaku kolapsu u černé díry, dosahují se nakonec v jejím nitru takové hustoty, které odpovídají hmotě ve stavu, který neznáme. Takový, který dokáží popsat jen obecnější teorie sjednocující popis interakcí a obsahují i kvantovou teorii gravitace. Tato hmota dokáže odolat tlaku v nitru černé díry a její nitro vytváří. Jaká je, zatím nevíme.
3) Ještě možná upřesnění. Pokud padá hmota k černé díře (ať už hvězdné nebo supermasivní), závisí její stav na průběhu dopadu a pokud při pádu do černé díry dosáhne velmi vysoké rychlosti a dochází k interakci s jinou hmotou, extrémnímu jejímu ohřátí (přemění se na plazma (pokud již jím nebyla)). Dochází tak k těm jevům, které u supernov nebo aktivních galaxií produkují výtrysky a vysokoenergetické záření. Ty závisí třeba i na tom, jak černá díra rotuje.
Re: Re: Re: Re: Re: Re: Trvání gravitačního záblesku
Zita Šustová,2020-09-10 07:24:53
Podle kvantové teorie pole ( tedy podle pana Brože, viz jeho příspěvek ) jsou totiž částice kvanty odpovídajících polí, tak např. foton je kvantum elektromagnetického pole, elektron či pozitron odpovídajícími kvanty spinorového pole popisujícího elektrony a pozitrony, gluon je kvantum pole silné interakce, atd.. A vzhledem k tmu co tu pan Brož řekl ( vzhledem i k tomu že řekl : diskuze tu jsou od toho, aby se téma co nejvíce vyložilo čtenářům, i s jejich pomocí :-), se ptám : a „z čeho“ jsou gravitační vlny ? jaká „kvanta“ nesou ty vlny, protože sám Brož říká, že „gravitační vlny odnáší energii“ a tedy nutně i nějakou formu hmotu, jakou ?, ptám se jakými částicemi je presentována hmota gravitačních vln ?? ( Ptám se s vědomím toho že se všude píše, že gr. vlny jsou jen !!!! zavlněním prostoru…takže : jak zavlnění prostoru může být energií ? )
Re: Re: Re: Re: Re: Re: Re: Trvání gravitačního záblesku
Pavel Brož,2020-09-10 12:04:34
Ano, paní Šustová, ačkoliv jsou nejen podle obecné teorie relativity, ale i podle drtivé většiny alternativních gravitačních teorií gravitační vlny "jenom" vlněním prostoru, tak přesto můžou přenášet energii. Současné detektory gravitačních vln jsou postaveny právě tak, aby detekovaly to vlnění prostoru, kdy se v jednom ze dvou směrů příčných k pohybu vlny vzdálenosti zkracují a v tom druhém prodlužují, a v opačné půlperiodě právě naopak. Konkrétnější představu, jak to funguje, si můžete udělat zde https://en.wikipedia.org/wiki/Gravitational_wave, doporučuji obrázky https://en.wikipedia.org/wiki/File:Quadrupol_Wave.gif a https://en.wikipedia.org/wiki/File:GravitationalWave_PlusPolarization.gif , a jak se toto střídavé prodlužování a zkracování vzdáleností využívá např. v detektoru LIGO viz zde https://en.wikipedia.org/wiki/LIGO , např. obrázek zde https://en.wikipedia.org/wiki/File:Gravitational_wave_observatory_principle.svg . Ta energie se tím vlněním prostoru přenáší právě tak, že to zkracování a prodlužování vzdáleností má dynamické důsledky na hmotu, kterou ta vlna prochází, a díky tomu můžeme tu vlnu detekovat. V případě LIGO tu detekci provádíme měřením interference světla po mnohonásobném průchodu ve Fabry-Perotově interferometru.
Co se týče kvant gravitačního pole, ta ještě nikdo nikdy jednotlivě nedetekoval. Jsme v situaci, v jaké byli fyzici na konci devatenáctého století, když uměli detekovat v různých částech spektra elektromagnetické vlny, ale neuměli ještě detekovat jejich jednotlivá kvanta, fotony. Teprve až Planck navrhl na začátku dvacátého století, že se elektromagnetické záření absorbuje a emituje v kvantech, díky kteréžto na svou dobu velice odvážné hypotéze vysvětlil vyzařování absolutně černého tělesa. O pár let později Einstein v souvislosti s objasněním příčiny fotoelektrického jevu přidal tvrzení, že elektromagnetické záření se v kvantech i šíří (kupodivu je to silnější tvrzení než Planckovo, protože v Planckově době byla představa, že i pokud má pravdu, tak že se při absorbci z elektromagnetické vlny, která sama může mít při pevné frekvenci energii spojitou, pouze ukrojí diskrétní kvantum energie, a při absorbci se zase diskrétní kvantum energie předá té spojité vlně, zatímco Einstein odmítl i tu představu elektromagnetické vlny mající při dané frekvenci libovolnou energii). Protože elektromagnetická vlna bez problémů interaguje s hmotou, netrvalo tak dlouho a byla detekována i jednotlivá kvanta elektromagnetického pole, pro která se ujal název fotony.
Analogicky s elektromagnetickým polem se předpokládá, že i gravitační pole má svá kvanta, která jsou nazvána gravitony, a která reprezentují šířící se gravitační vlnu analogicky jako fotony reprezentují vlnu elektromagnetickou. Typická elektromagnetická vlna, např. když ji zaznamenáváme prostým okem jako světlo, sestává z obrovského množství fotonů (v případě detekce okem jde až o statisíce biliónů fotonů za sekundu), pokud ale chceme detekovat jednotlivé fotony, vyžaduje to velice sofistikovaná zařízení, ve kterých se nejčastěji připravují zdroje světla tak, aby byla vysoká pravděpodobnost, že se v okamžiku detekce v detektoru nalézá jenom jeden foton, a toto zeslabené světlo se pak detekuje. Stávající detektory fotonů totiž neumí spolehlivě rozlišit mezi případem, kdy jimi prošel jeden foton nebo fotonů více, on ten detektor prostě vydá v případě detekce signál v obou případech, je tedy nutné to světlo dostatečně zeslabit pokud chceme detekovat jednotlivé fotony a ne skupiny mnoha fotonů.
No a dnes jsme s gravitačními vlnami v podobné situaci, jako když fyzici uměli detekovat makroskopické elektromagnetické vlny, ale ještě neuměli detekovat jednotlivé fotony. Na detekci jednotlivých gravitonů a tím i na jejich experimentální důkaz si ale počkáme velice dlouho, osobně pochybuji, že se to podaří do konce tohoto století, právě proto, jak strašně slabě gravitace působí na hmotu, pokud to poměřujeme silou ostatních interakcí. Detektor jednotlivých gravitonů prostě bude ještě hodně dlouho scifi, oproti tomu detektor jednotlivých fotonů je dnes běžnou součástí všech optických laboratoří.
Každopádně to, že by i gravitační pole mělo být kvantováno podobně jako je kvantováno pole elektromagnetické i všechna ostatní pole, je v dnešní době stále jen hypotéza. Z dnešního pohledu to vidíme tak, že to nemůže být jinak, že když všechna ostatní pole jsou kvantována, tak musí být kvantováno i pole gravitační, dokonce jsme si už vymysleli jméno pro to kvantum, graviton. Ovšem příroda už mnohokrát uštědřila vědcům lekci tehdy, když si byli něčím příliš jisti, a ukázala, že věci mohou být i jinak než jak se to v dané době jeví jako nejlogičtější. Navíc zde máme jisté podstatné rozdíly mezi gravitační interakcí a interakcemi ostatními - ostatní interakce mají lokalizovatelné energie, ale gravitační ne. Ostatní interakce nelze lokálně vynulovat přechodem do volně padající soustavy, ale gravitační ano. Ostatní interakce jsou renormalizovatelné, což znamená, že v odpovídajících kvantově polních teoriích vzniká jen konečný počet problematických členů rostoucích nade všechny meze (lidově řečeno nekonečen), se kterými si teorie musí poradit, aby byla schopna dávat měřitelné výsledky (přičemž každému takovému členu ve výsledku odpovídá ztráta schopnosti ho předpovědět a jeho hodnota musí být vzata z experimentu bez možnosti jej porovnat s teorií), nicméně gravitační interakce renormalizovatelná není, což znamená, že podobných členů je v odpovídající kvantové verzi nekonečně mnoho. Gravitace má také vliv na chod času a dilatace délek v gravitačním poli, ale ostatní interakce žádný takový vliv nemají. Prostě gravitace je v mnoha ohledech zcela jiná než ostatní interakce, a dokud nebudeme umět detekovat jednotlivé gravitony, což se nemusí podařit ještě dlouhé desítky let, tak nebudeme mít ani jistotu, že gravitační pole je stejně jako ostatní pole kvantované.
Re: Re: Re: Re: Re: Re: Re: Re: Trvání gravitačního záblesku
Zita Šustová,2020-09-11 08:16:12
Já Vám děkuji za tak rozsáhlou a obsáhlou odpověď. Která mi přecejen evokovala dalších několik otázek :
a) V podstatě říkáte, že gravitační vlny nesou-unáší-přenáší gravitony ( potažmo hmotu-energii) jen je nevidíme, ještě neumíme vidět-detekovat…; čili samotná vlna délkové dimenze ( kterou detekuje LIGO ) by nemohla být a není energií. Je to tak ?
b) Nese-li gravitační vlna, vlna pulzujícího prostoru gravitony, pak ty gravitony musely být i v té původní předsrážkové „díře“? Je to tak?
c) ČD vznikala ve vesmíru postupně, a tak než byla ČD plně hotová musela být z jiného materiálu než jsou gravitony (je to tak ?)…a tedy jaký materiál byl v té kouli, která se později stala černou dírou ? Jak se v ČD měnil materiál různorodý na gravitony ?
d) Když padají materiály různých hmot do ČD, která hltá jakýkoliv materiál i mnoho miliard let, jak se tento pestrý materiál změní v „díře“ na gravitony ?
e) mluví se o tom, že „z česné díry nemůže vyletět žádný foton“, jenže.. když v ČD žádné fotony nejsou, jen gravitony !!, tak ani vyletět nemůžou, že, logicky ?!?! Je to tak ?
f) Říkáte, že detektory detekují pouze zavlnění prostoru, nikoliv gravitony…to prý potrvá ještě 100 let než budeme moci detekovat gravitony, čili do té doby je to stále experimentem nepotvrzená hypotéza, matematicky navěky platná. Takže 100 let ještě nebudeme vědět „co“ je v černé díře za materiál !!
g) Říkáte, cituji : Ta energie se tím vlněním prostoru přenáší právě tak, že to zkracování a prodlužování vzdáleností má dynamické důsledky na hmotu, kterou ta vlna prochází, a díky tomu můžeme tu vlnu detekovat.“ Když se nad tím zamyslím, tak tu máme „nějakou energii“ ( balík energie ) a ta je p ř e n á š e n a = nesena vlnou délkové dimenze respektive vlnami tří dimenzí prostoru. Kdysi Einstein zakázal éter, že elmg. vlnění ho nepotřebuje, a…a nyní „nějaký balík energie z gravitonů“ potřebuje (?) na přenos energie někam vlnění samotného prostoru ?…,
h) Dále říkáte : “Co se týče kvant (gravitonů) gravitačního pole, ta ještě nikdo nikdy jednotlivě nedetekoval. Jsme v situaci, v jaké byli fyzici na konci devatenáctého století, když uměli detekovat v různých částech spektra elektromagnetické vlny, ale neuměli ještě detekovat jejich jednotlivá kvanta, fotony“ Pozor, tady odkláníte řeč na původní otázku. Otázky byly na vlny, na gr. vlny néé na gravitační pole. Anebo snad chcete říci, že „pole“ je totéž co „vlny“ ???? Proč gravitační pole detekujeme tak snadno a gravitační vlny jsme detekovali až po strašném úsilí ?
ch) Říkáte : „Navíc zde máme jisté podstatné rozdíly mezi gravitační interakcí a interakcemi ostatními“ Zeptám se : když se srazí dvě ČD je to také interakce ? gravitační interakce ?
i) Dále říkáte : „Ostatní interakce jsou renormalizovatelné, což znamená, že v odpovídajících kvantově polních teoriích vzniká jen konečný počet problematických členů rostoucích nade všechny meze (lidově řečeno nekonečen), se kterými si teorie musí poradit, aby byla schopna dávat měřitelné výsledky“. Zeptám se : my fyzikové abychom mohli „něco“ měřit musíme počkat na přírodu až ona si nějaké ty interakce zrenormalizuje ? Jinak : bez zrenormlizování rovnic ( fyziků na papíře, abstraktních ) příroda nemůže existovat a člověk nemůže nic měřit ? Dokud my nemáme zrenormalizované rovnice-teorii, tak je příroda špatně ?
j) Poslední otázka , říkáte :“ Gravitace má také vliv na chod času a dilatace délek v gravitačním poli, ale ostatní interakce žádný takový vliv nemají.“ Pro výklad STR je důležitý zahajovací „rovnoměrný přímočarý pohyb“ tělesa ( rakety nebo kvasahu u konce pozorovatelného vesmíru atd.) m .v Jakmile se změní tento rovnoměrný pohyb „m.v“ na „m.a“, ( působením jakékoliv interakce ) tedy na nerovnoměrný-zrychlený pohyb, pak to zrychlení je fyzikálně ekvivalentní gravitačnímu zrychlení. Ano ? Čili abychom v STR mohli vy-sledovat dilataci ( kontrakci) musí se véé malé postupně měnit na véé velké, až se blížící céé, pak začne být v té STR „čitelná“ dilatace (kontrakce ) Čili v STR se řada rychlostí v(1), v(2) v(3), v(4) až v(n) mění skokově na v(n) se blíží cééé pomocí zrychlení-zrychlování „a“…,což nemusí být jen „gravitační“ zrychlení…ano nebo ne ? STR je jen „stop-stavem“ ve zrychleném, neinerciálním pohybu, až se véé dostane k cééé, a pak pozorujeme dilatace. Proč má jen gravitace „vliv“ na vznik dilatace ?? Nelze těleso urychlit na véé se blíží cééé jinak než gravitací ?? Já sem jen hloupá holka, já se ptám chytrých.
Anti Sarlatan
,2020-09-11 09:23:28
Já sem jen hloupá holka, já se ptám chytrých - Nie, nie si 'hloupá holka'. Si Josef Navratil, stary stalker, co sa marne schovava za roznymi nickmi. Prestan otravovat svojimi prispevkami kazdu rozumnu diskusiu a strc si svoju HDV do dvojvelicinovej *****.
Pavel Brož
,2020-09-11 12:11:02
Jo tak takhle to je, pane Navratile, mě pořád vrtalo hlavou, odkud je mi ten Váš styl tak povědomý, a kdyby to tu nenapsal jiný komentátor, tak by mi to vrtalo hlavou ještě hodně dlouho. Není Vám to trapné, skrývat se pod nicky, zvláště když jsem Vám kdysi věnoval takového času v nekonečných emailových diskuzích, které ve Vašem případě stejně k ničemu nevedly? A mého kamaráda, který s Vámi strávil ještě více času, jste nakonec dotáhnul až k soudu.
Takže pane Navrátile, tuto diskuzi považujte za ukončenou.
černé díry
Pavel Ouběch,2020-09-04 08:18:08
Zajímavé (kromě mnoha dalších věcí) na tom všem je, že kdyby veškerá hmotnost černých děr nebyla pod jejich horizontem, ale nad ním, pozorovali bychom pravděpodobně úplně to samé.
Nebo existuje pozorování, které by tuto možnost vyloučilo ?
Re: černé díry
Pavel Hudecek,2020-09-05 10:27:34
Ano, např jakékoli pozorování splynutí ČD a vlastně i sama existence ČD, která je evidentně větší, než když vznikla. I kdyby se hmota nemohla nořit dovnitř a zůstávala na poloměru kam byla přisáta, bude se horizont přibývající hmotou zvětšovat, takže hmota pozřená podle Vaší myšlenky se bude nacházet v různých hloubkách, podle toho, kdy přibyla.
Kdyby to fungovalo podle Vás, musel by existovat mechanizmus, který by starou hmotu při růstu ČD tahal nahoru a udržoval na povrchu.
Re: Re: černé díry
Pavel Ouběch,2020-09-06 08:24:11
A co takhle moment hybnosti - resp. setrvačnost. Ten se ani při a po splynutí ČD ztratit ani zmenšit nemůže.
Re: Re: Re: černé díry
Pavel Hudecek,2020-09-06 11:18:56
Proto se tak nějak předpokládá, že všechny, nebo drtivá většina ČD ve vesmíru je rotujících. Tím pádem mají ke Swarchildově klidné kuličce dost daleko. Jsou to pak Kerrovy ČD, nad horizontem mají ještě ergosféru a tak je okolo nich poněkud živěji. Další argument proti idealizovanému lepení na povrch.
Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-07 11:29:45
To, že všechny ČD rotují, je celkem zřejmé. Dokládají to detekované gravitační vlny z jejich splynutí.
Naproti tomu Kerrovo řešení (které např. nezahrnuje rozložení hmoty nad horizontem) pro rotující ČD je pouhá neověřená hypotéza. Je to sice určité řešení rovnic OTR, která je v mnoha a mnoha případech ověřena, ale faktem je, že každá teorie má své limity. U OTR dobře známá limita neslučitelnosti s kvantovou mechanikou.
- O dalších nevíme, ale to neznamená, že neexistují. Proto se každá teorie - i OTR - musí ověřovat ve všech svých predikcích.
Proto u otázky, jestli je hmota ČD pro vzdálené pozorovatele (což jsme my a drtivá většina celého vesmíru) pod nebo nad horizontem vůbec nejde o (libovolnou) teorii, ale jen o pozorování.
Proto ta moje počáteční otázka.
Ještě k tomu horizontu. Faktem je, že podle zvolených souřadnic se může jeho průměr pro vzdáleného pozorovatele například posunout, ale to není z logiky věci nic divného. Neznamená to ale, že neexistuje.
Ale především. Žádné souřadnice nemají nic společného s fyzikální realitou !
Proto je například příspěvek pana Brože výše v některých směrech zavádějící. Je úplně jedno, jaké souřadnice si zvolím, jestli isotropní Weylovy nebo nějaké úplně jiné. V případě ČD záleží jen na tom, jestli jde o vzdáleného pozorovatele (= prakticky celý vesmír) nebo o pozorovatele padajícího do ČD.
Když pozorujeme splynutí černých děr, jsme vzdálení pozorovatelé. Rozhodující je vždy experiment.
Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-07 13:41:39
Pane Ouběchu, mě vždycky pobaví, když se k otázkám platnosti či neplatnosti těch kterých predikcí libovolné teorie kriticky vyjadřují ti, kteří tu teorii neovládají ani v té míře, aby z ní absolvovali vysokoškoloskou zkouškou, což je zrovna Váš případ. Dobře, ještě bych chápal, že ten dotyčný kritik sice nemá zkoušku z té teorie, ale dokonale jí ovládá. Jenže ani to není Váš případ, jak jste už prokázal vyslovením spousty nesmyslných tvrzení v diskuzi zde https://www.osel.cz/11216-co-kolem-ceho-obiha-opravdu-a-snad-i-skutecne.html .
Pokud máte svou vlastní teorii, která opravuje obecnou teorii relativity v jejích předpovědích pro distribuci hmoty ať už rotujících či nerotujících černých děr nad jejich horizontem, sem s ní. Včetně rovnic, ve kterých se tato teorie odlišuje od obecné relativity a z nich odvozených predikcí kolidujících s predikcemi OTR. Pokud takovouto teorii nemáte, tak je Vaše poznámka pouze na úrovni hospodských výroků, že ono je to stejně jinak, než ti odborníci tvrdí, přičemž se nedodá jak to teda je.
Aby nevznikla mýlka, obecná relativita je pouze teorie, o tom není sporu. Existuje neuvěřitelné množství jiných gravitačních teorií, o kterých bych zde mohl dlouze referovat, kde a v čem se shodují s OTR a kde a v čem ne. Uměl bych o nich referovat, Vy ne.
Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-07 14:48:23
Pane Broži, asi jste si mě s někým spletl. Moje otázka zněla (a zní), jestli lze pozorováním zjistit, zda se hmota ČD nachází pod nebo nad horizontem. Jde jen o moji zvědavost, žádné tvrzení.
- Bohužel, na to odpověď zatím nemám.
Když jsme u té minulé debaty - s jistým úsilím se mi podařilo knihu K.Kuchaře - základy OTR vypůjčit. Vztah, který jste z jeho knihy citoval pro GPS družice v grav. poli Země na oběžné dráze pan Kuchař odvodil pro neinerciální systémy - ne pro zakřivený časoprostor.
Jinak - na str. 184 pan Kuchař píše: "... položíme-li (hmotnou) kuličku zavěšenou na spirále do místa s nižším gravitačním potenciálem, hmota kuličky se zvětší ...."
- to se mi zdá velmi, velmi podezřelé, spíš nemožné.
Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-07 23:03:41
Co se týče toho, že se Vám zdá podezřelé či dokonce nemožné, že hmotnost tělesa se jeho umístěním do nižšího gravitačního potenciálu zvýší, tak toto je jeden z nejznámějších a dokonce nejvíce zpopularizovaných jevů obecné teorie relativity, dokonce i u českých hospodyněk to svého času zpopularizoval Jiří Grygar ve svém úchvatném seriálu Okna vesmíru dokořán. Pamatuji si, jak jsem poté všem ženským v široké rodině musel vysvětlovat, že jde o zanedbatelný efekt (s dvojsmyslným dodatkem, že v jejich případě to už vůbec nemá smysl řešit).
Každopádně toto zvýšení hmotnosti tělesa v nižším gravitačním potenciálu (tj. např. jeho přiblížením k jiné hmotě) plyne např. ze vztahu (III.15) na straně 131 oné Kuchařovy učebnice (máme oba stejné vydání, Karel Kuchař totiž po roce 1968 emigroval, takže žádné další vydání jeho učebnice za bolševika nebylo). Zmíněný vztah (III.15) lze odvodit dosazením za dt/dtau ve vztahu (III.14), a vztah dt/dtau (uveden explicitně také ve vztahu (III.13)) je odvozen dříve coby vztah (I.36) na straně 66, k jeho odvození včetně pochopení kontextu je nejlepší začít už od strany 50, nejpozději od strany 59, nebudu zde všechny ty stránky reprodukovat. Samotné odvození vztahu dt/dtau je formálně velice snadné, vyjde se z obecného tvaru prostoročasového intervalu ve tvaru ds^2=g_mí_ný*dx_mí*dx_ný (mí, ný jsou řecké prostoročasové indexy jako v té učebnici) – nejde ale jen o to formální odvození, jde i o to vědět, jaká je interpretace těch kterých výrazů, proto je tomu věnována celá kapitola „Prostoročasová měření v neinerciálních soustavách“.
Jinak co se týče té kapitoly, odkud citujete tu větu ze strany 184, konkrétně se jedná o kapitolu „Model ideálních hodin v obecné teorii relativity“, tak tam by se hodilo k tomu přidat pár poznámek. Z pohledu dnešní výuky obecné relativity (a nejen dnešní, ale i z pohledu výuky během mých studií před třiceti lety) je tato kapitola takový trochu muzeální kousek. Náš přednášející nám už tehdy říkal, že těmto věcem kolem konstrukcí ideálních hodin, ideálních měřítek atd., se už dávno nepřikládá takový význam, jako v prvních desítkách let rozvíjení obecné teorie relativity, protože nakonec převážil pohled algebraicko-geometrický, kdy se zdůrazňují spíše ty formální matematické konstrukty jako jsou diferencovatelné variety, Riemannovy a pseudo-Riemannovy prostory a jejich vlastnosti, rovnice struktury, diferenciální formy na křivých prostorech, atd.. Ten algebraicko-geometrický pohled sice má své výhody, zejména v okamžiku, kdy se hledají možná zobecnění obecné relativity schopná pokrýt i zbývající interakce (kdy se využívají i zobecnění na tzv. superprostory nebo na nekomutativní geometrii), protože hodně z těch formálních algebraicko-geometrických vztahů lze totiž opravdu zobecnit i na tyto exotické prostory. Nicméně zúžení té problematiky jenom na ten algebraicko-geometrický pohled má taky své nevýhody, např. tu, že není jasné, jak na těchto exotických prostorech prakticky realizovat měření délek a času. Na konci mého studia se pár mých přátel vrhlo právě na studium nekomutativní geometrie v očekávání, že tento obor v příštích lete zažije vědecký boom (nezažil). Nikdo z nich mi nebyl schopen odpovědět na otázku, jak se v prostoru, ve kterém součin šířky a výšky závisí na jejich pořadí (přičemž nejde jen o změnu znaménka), měří vzdálenosti, natož jak se v nekomutativním prostoročasu měří čas. Jednoduše tyto otázky odmítali s tím, že pro ně nejsou podstatné, že důležitější jsou ta formální zobecnění těch vztahů platících pro Riemannovy a pseudo-Riemannovy prostory.
Proto si osobně myslím, že ve skutečnosti ty dávno vybudované základy obecné relativity stojící na detailním rozboru problematiky měření délek a času v křivých prostoročasech – a v tomto je právě ta Kuchařova učebnice jedinečná, protože pochází z doby, kdy ten počáteční pohled stále ještě převažoval, dnes už ty učebnice OTR opravdu dávají důraz převážně na ty algebraicko-geometrické aspekty – jsou i v dnešní době velice aktuální. Mohu porovnávat mezi různými přístupy, tak např. učebnice Gravitation od Charlese W. Misnera, Kipa S. Thorna a Johna A. Wheelera, která vyšla v roce 1973, tedy jen šest let po vydání Kuchařovy učebnice, už dává důraz na něco úplně jiného než Karel Kuchař, a pokud člověk pokročí k ještě mladším dílům typu Spinors and Space-time od Rogera Penrose a Wolfganga Rindlera, tak tam už o nějaké měření délek a času nezakopne ani náhodou, tam už je to čistá geometrie, sice podaná ve velice atraktivním spinorovém hávu, nicméně to už má mnohem blíže k čisté matematice než k fyzice.
To jenom na vysvětlení toho, proč tyto kapitoly a také kapitola věnovaná formálnímu modelu ideálních hodin v obecné relativitě, kterou má ve své učebnici Kuchař, jsou z pohledu dnešní výuky dosti muzeální. Osobně si ale myslím, že jsou ve skutečnosti stále velice aktuální. Konkrétně třeba tu kapitolu popisující model ideálních hodin napsal Kuchař z toho důvodu, aby demonstroval, že předchozí formální popisy měření času jsou také fyzikálně realizovatelné. On to sám v úvodu té kapitoly píše, že předtím to měření délek a času popisoval z fenomenologického pohledu. Vznikl by ovšem docela trapas, kdyby se pak ukázalo, že hodiny s vlastnostmi odvozenými předtím fenomenologicky nejdou fyzikálně realizovat, resp. že pokud se zkonstruují hodiny, u kterých byl předpoklad, že budou dobrým přiblížením ideálních hodin, tak že budou odměřovat čas úplně jinak. Proto se v té kapitole věnuje taková pozornost důkazu, že hodiny, které mohou sloužit jako ideální hodiny v plochém prostoročase (konkrétně harmonický oscilátor), budou měřit čas takovým způsobem, který bude ve shodě s předtím fenomenologicky odvozenými vztahy. Vlastně to může být chápáno jako jakýsi test vnitřní konzistence té teorie, totiž že formálně odvozené časové dilatace jsou taktéž získány nikoliv jen na základě fenomenologického rozboru prostoročasových vztahů, ale také na základě řešení pohybových rovnic pro model ideálních hodin. Tento test vnitřní konzistence je z moderní výuky obecné relativity vypuštěn, což je podle mě škoda.
Ještě se zmíním k té Vaší poznámce, že vztah, který jsem citoval z té učebnice, Kuchař odvodil pro neinerciální systémy, ne pro křivý prostoročas. To je naprosto v pořádku, protože obecná relativita je postavená na principu ekvivalence, podle kterého je gravitace lokálně ekvivalentní setrvačnému zrychlení pociťovanému v neinerciální soustavě. Proto když se hledá obecně-relativistická forma fyzikálních zákonů, v drtivé většině případů stačí, když se najde jejich forma v neinerciálních soustavách, protože tím se najde i jejich forma lokálně platná v gravitačním poli, tedy v křivém prostoročase. V praxi se tato obecně-relativistická forma nejsnáze nalezne tak, že se vyjde ze speciálně-relativistické formy, a všechny parciální derivace se nahradí derivacemi kovariantními. Tento postup se také nazývá jako tzv. minimální vazba, čímž se míní, že se do fyzikálních zákonů pokud možno přidávají jen takové konstrukce z metrického tenzoru, které se dají vynulovat přechodem do padající soustavy, což je právě požadavek principu ekvivalence, aby se gravitační pole dalo lokálně vynulovat. Obecněji bychom totiž mohli speciálně-relativistické zákony zobecňovat na zákony platné v zakřiveném prostoročase nekonečně mnoha způsoby, tak např. bychom ke každému fyzikálnímu zákonu mohli přidat libovolné množství členů úměrných jakékoliv kladné mocnině křivosti prostoročasu - všechny tyto navzájem odlišné vztahy by samozřejmě v plochém prostoročasu přešly v jeden společný starý známý speciálně-relativistický vztah. Ovšem v křivém prostoročase bychom přechodem do volně padající soustavy nedostali tyto speciálně-relativistické vztahy, protože by tam stále byly navíc ty členy s křivostí, které se přechodem do padající soustavy nevynulují – jinými slovy, pak by neplatil princip ekvivalence, který žádá, aby soustava volně padající v gravitačním poli byla lokálně nerozlišitelná od soustavy inerciální. Takže princip ekvivalence je přesně ten důvod, proč je tvar fyzikálních zákonů v obecné relativitě formálně identický s tvarem fyzikálních zákonů v neinerciálních soustavách.
Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Marek Fucila,2020-09-08 02:35:41
Asi to nie je úplne k veci. Z rýchleho googlenia o nekomutatívnej geometrii som nezískal predstavu ako by taký svet vyzeral, ale pripomenulo mi to nedávne videá, ktoré som videl a možno by niekoho zaujímli.
Ako by vyzeral svet v sférickej geometrii:
https://youtu.be/yY9GAyJtuJ0
A ako v hyperbolickej:
https://youtu.be/pXWRYpdYc7Q
A ako by vyzerali relativistické efekty, keby sme sa pohybovali rýchlosťou blízkou rýchlosti svetla: https://youtu.be/udqihUBGuZ8
Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Marek Fucila,2020-09-08 02:40:39
A ešte som zabudol na staršie video, kde vytvoril ten neeuklidovský engine a ako to vyzerá, keď v geometrii záleží na tom, akým smerovm sa človek pohybuje:
https://youtu.be/kEB11PQ9Eo8
Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-08 12:33:52
Nevím, co všechno si myslí české hospodyňky :-) , ale myslím, že Ernst Mach by měl nezřízenou radost, kdyby se potvrdilo, že v blízkosti velkých hmotností je větší i klidová hmotnost pozorovatele.
Škoda, že se toho nedožil.
Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-08 13:28:11
No, myslím, že si Ernsta Macha poněkud idealizujete. Ony se sice dokonce občas konají i konference, na kterých se pějou oslavné ódy na filosofický přínos Macha, a sám Einstein se dlouho snažil na Machově principu postavit svou obecnou relativitu, než to finálně vzdal. Ernst Mach byl ve skutečnosti přesně taková názorová konzerva, jaké Einstein ještě coby mladý student bytostně nesnášel a s nimiž měl kvůli tomu na škole dost podstatné konflikty. Ernst Mach například do konce svého života tvrdohlavě odmítal existenci atomů, kteroužto myšlenku všemožně zesměšňoval. To, že se přesto zrovna Mach stal v Einsteinově dospělosti jeho oblíbencem lze pouze považovat za typický příklad ironie dějin.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-08 18:07:34
No, já to myslel tak, že ze změny chodu času při rozdílu grav. potenciálu automaticky neplyne změna hmotnosti. K té je ještě potřeba pohyb.
Jinak řečeno, vlastní hmotnost objektu se na různých potenciálních hladinách gravitačního pole nemění.
Řekl bych, že právě to je ten případ, kdy nejde využít principu ekvivalence. - To mi zatím pan Kuchař nevyvrátil.
Na obhajobu Ernsta Macha by bylo dobré zmínit, že on odmítal přijmout cokoliv, co nebylo možné přímo změřit. Někdy měl pravdu - odmítal Newtonův absolutní prostor, vůči kterému mělo rotovat vědro s vodou, ale bohužel odmítal atomy, které v té době byly nedetekovatelné.
Mimochodem, pokud bychom v experimentu s vědrem vody nepřijali Machovu myšlenku, vůbec netušíme, vůči čemu to vědro vlastně rotuje.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-08 22:01:31
Cílem Karla Kuchaře nebylo Vám něco vyvracet, nebylo to cílem ani Alberta Einsteina jakožto tvůrce obecné relativity, a není to obecně ani cíl ani povinnost autora žádné teorie cokoliv někomu vyvracet. Obecná teorie relativity je dobře etablovaná teorie, během více než sto let její existence tisíce odborníků zkoumalo, zda je jakožto teorie matematicky vnitřně konzistentní (bylo shledáno, že je), tisíce jiných odborníků participovalo na experimentech, které měly potvrdit či vyvrátit předpovědi OTR (všechny dosavadní testy dopadly ve prospěch této teorie). To je opravdu vše, co se od úspěšné teorie očekává, jednak její matematická vnitřní konzistence, jednak shoda jejích předpovědí s experimentem. Nic víc, nikomu není potřeba nic vyvracet.
Jedním z důsledků obecné teorie relativity je to, že hmotnost se mění nejen v důsledku rychlosti, což odvodila už speciální teorie relativity která gravitaci popsat neumí, ale také i v důsledku změny jeho umístění v gravitačním poli. S principem ekvivalence to souvisí tak, že ten nám říká, jaký je tvar fyzikálních zákonů v křivém prostoročase (že je totiž formálně stejný jako ve zrychlené soustavě), a do toho zákona pak dosadíme derivaci souřadnicového času podle vlastního času tělesa (výše zmíněné dt/dtau), který odvodíme ze tvaru prostoročasového intervalu v křivém prostoročase. Není potřeba nikomu nic vyvracet, stačí tu teorii znát a umět z ní odvozovat její predikce, není v tom žádné kouzlo, jenom znalost té teorie a potřebné matematiky.
Vědro rotuje vůči lokální inerciální soustavě. Není k tomu potřeba ani Newtonova absolutního prostoru, ani vzdálených hvězd a la Machův princip, je to lokální záležitost.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-09 10:22:26
Těžko mohlo být cílem Karla Kuchaře a Alberta Einsteina mi něco vyvracet, když mě neznali :-)
(Škoda, že jsem neměl možnost poznat osobně já je.)
- A samozřejmě, něco vyvrátit nemůže žádná teorie, ale jen experiment. Takže jen blázen by se pokoušel sestrojit teorii za účelem něco vyvracet.
V ostatních názorech výše se ale hluboce mýlíte.
Dilatace času a ostatní příbuzné efekty jsou v neinerciálních soustavách pozorovatelné jen proto, že lze každou neinerciální soustavu "rozsekat" na dostatečně malé soustavy inerciální, kde jsou tyto efekty popsány STR.
Zrychlení samo nemá na chod času, atd. žádný vliv. To je experimentálně ověřeno do a = 10E28 m/s2.
Proto se ani nemůže měnit hmotnost v závislosti pouze na hodnotě gravitačního potenciálu.
Mimochodem, gravitační potenciál je veličina poměrová, ne absolutní. Takže - pokud by jste měl vy a nejspíš i pan Kuchař pravdu, testovací objekt by měl zároveň mnoho různých hmotností, podle toho, jaký by byl rozdíl gravitačního potenciálu mezi objektem a pozorovatelem.
Ano, OTR je matematicky konzistentní a v mnoha směrech relevantní teorie. Jenomže při její aplikaci jde také o interpretaci. Tam se často dělají chyby.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-09 23:05:00
Pane Ouběchu, opět jako už v diskuzi zde https://www.osel.cz/11216-co-kolem-ceho-obiha-opravdu-a-snad-i-skutecne.html i nyní bohužel prokazujete podstatné neznalosti problematiky. Píšete cituji „Zrychlení samo nemá na chod času, atd. žádný vliv. To je experimentálně ověřeno do a = 10E28 m/s2“, jenže zapomínáte dodat to podstatné, že to platí pro pozorování v inerciální soustavě. Pokud pozorujeme dilatační efekty a vliv na setrvačnou hmotnost tělesa, tak v inerciální soustavě opravdu platí, že zrychlení tělesa nijak neovlivňuje tyto jevy. Tzn. že pro tyto jevy aplikujeme Lorentzův faktor 1/odm[1-v^2/c^2], ve kterém figuruje pouze rychlost tělesa v té inerciální soustavě, velikost té dilatace ale už nijak nezávisí na zrychlení tělesa.
Jenže tady se bavíme o soustavách neinerciálních, a v těch má metrický tenzor jiný tvar, než jaký má v inerciálních soustavách, a skrze něj se pak uplatňují dilatační efekty, ve kterých figuruje buď tvar toho gravitačního pole – to pokud je neinerciálnost té soustavy dána gravitací - anebo zrychlení té neinerciální soustavy vůči inerciální – to pokud je neinerciálnost té soustavy dána jejím zrychlením, event. může jít i o kombinaci gravitace a zrychlení.
Pojďme si ilustrovat, jak konkrétně se tato odlišnost mezi tím, že zrychlení nemá vliv na chod hodin v inerciální soustavě, kontra že naopak má vliv na chod hodin v neinerciální soustavě, projeví v případě řešení paradoxu hodin v rotující soustavě. Mimochodem, řešení toho paradoxu je popsáno na straně 148 té Kuchařovy učebnice. Připomenu podstatu toho paradoxu – máme pozorovatele stojícího v inerciální soustavě, a druhého pozorovatele umístěného na točícím se kolotoči, tedy v soustavě neinerciální. Předpokládáme, že kolotoč se točí natolik rychle, abychom byli schopni registrovat relativistickou dilataci času dvojicí hodin, jedněmi stojícími v inerciální soustavě, a druhými točícími se na kolotoči – mimochodem, v první polovině devatenáctého století to byla ještě naprosto nesplnitelná podmínka, nicméně v dnešní době, kdy disponujeme extrémně přesnými atomovými hodinami schopnými měřit čas s přesností lepší než 10^-14, už se to dá aspoň principiálně zařídit i u dostatečně pomalých rotací s obvodovou rychlostí nad 100 m/s, tak např. rotory ve velkých elektrárenských generátorech dosahují větších obvodových rychlostí (slovo principiálně je důležité, samozřejmě že v praxi nikdo neinstaluje špičkové atomové hodiny na rotor generátoru).
Paradox spočívá v tom, že stojící pozorovatel vidí, jak se vůči němu zpomalují hodiny točícího se pozorovatele, protože ten se vůči němu pohybuje rychlostí v=omega*r, kde omega je úhlová rychlost kolotoče a r je jeho poloměr. Stojící pozorovatel tedy vidí, že v důsledku relativistické kontrakce se chod hodin na kolotoči zpomalí faktorem odm[1-v^2/c^2], tzn. že za n sekund podle hodin stojícího pozorovatele uplyne na kolotočových hodinách pouze n*odm[1-v^2/c^2] sekund. Rotující pozorovatel sice zažívá i zrychlení, ale stojící pozorovatel na toto zrychlení nemusí brát zřetel, protože V INERCIÁLNÍ SOUSTAVĚ NEMÁ ZRYCHLENÍ TĚLESA VLIV NA CHOD JEHO HODIN. Napsal jsem kapitálkami slova, která jsou v tom tvrzení nezbytná pro jeho platnost. Stojící pozorovatel ale usoudí, že stejně tak, jako on vidí, že pozorovatel na kolotoči se kolem něho pohybuje po kružnici, tak stejně tak se z pohledu pozorovatele na kolotoči pohybuje po kružnici on, takže tím pádem by pozorovatel na kolotoči mohl udělat úplně stejný výpočet a dojít k úplně stejnému závěru, totiž že se naopak musí zpomalovat hodiny stojícího pozorovatele. Jenže ony se ve skutečnosti zpomalují jenom jedny hodiny, a to jsou ty, které jsou na kolotoči, a dokonce i točící se pozorovatel to může zjistit díky tomu, že opakovaně míjí hodiny stojícího pozorovatele. A v tom je právě ten paradox, protože pokud bychom brali v potaz jenom tu relativistickou kontrakci a nic jiného, dospěli bychom k závěru, že oba pozorovatelé vidí, jak se hodiny toho druhého vůči jeho vlastním zpomalují - jenže toto ve skutečnosti nenastává, logicky ani nemůže (v okamžiku, kdy se hodiny míjí, tak se jednoznačně zjistí které se zpomalily).
Takže ten stojící pozorovatel bude chtít vědět, jak mu to ten točící se pozorovatel vysvětlí, že z kolotoče vidí, že hodiny mimo kolotoč se vůči kolotočovým nezpožďují, ale naopak předbíhají. Vysvětlení je následující – soustava kolotoče je soustavou neinerciální, a díky tomu v ní vypadá jinak metrika prostoročasu. Tato metrika je popsána po provedení 3+1 rozkladu prostoročasu na straně 148 dole v té Kuchařově učebnici, nebudu ji zde opisovat, protože tu učebnici máte, jenom upozorním na to, že složky této metriky závisí na úhlové rychlosti omega, která udává i velikost zrychlení té neinerciální soustavy. V neinerciálních soustavách působí na chod hodin nejen rychlost tělesa, ale také složky té metriky, a výsledkem je to, že místo toho, aby se hodiny mimo kolotoč vůči kolotočovým hodinám zpožďovaly, budou se naopak předbíhat. Příslušné odvození je na straně 149.
Takže v tomto to je - zrychlení tělesa sice nemá vliv na chod jeho hodin, ale toto platí pouze při pozorování v inerciální soustavě. Proto stojící pozorovatel pozoruje, že se hodiny na točícím se kolotoči zpožďují. Tvrzení, že zrychlení nemá vliv na chod hodin, ale neplatí v soustavě neinerciální, protože v neinerciální soustavě má metrika jiný tvar než v soustavě inerciální a díky tomu se uplatní i jiné vlivy na chod hodin, které se v inerciální soustavě uplatnit nemohou. Jak konkrétně metrika ovlivní chod hodin se odvozuje v kapitole I.3 „Prostoročasová měření v neinerciálních soustavách“ v té Kuchařově učebnici. Vliv metriky vede ke zpožďování hodin buďto ve zrychleně se pohybující neinerciální soustavě, anebo v neinerciální soustavě způsobené přítomností gravitačního pole – připomínám, že podle principu ekvivalence jsou oba tyto vlivy lokálně rovnocenné.
Takže toto bylo ohledně Vašeho tvrzení, že zrychlení samo nemá vliv na chod času, a proto se ani nemůže měnit hmotnost v závislosti na gravitačním potenciálu. Ve skutečnosti zrychlení nemá vliv na chod času pouze když pozorujeme zrychleně se pohybující těleso v inerciální soustavě, jenže v inerciální soustavě žádný gravitační potenciál není. Pokud ho pozorujeme v gravitačním poli, tak v něm pro změnu neexistuje inerciální soustava (připomínám, že přechodem do volně padající, tedy do lokálně inerciální soustavy, gravitaci lokálně vynulujeme).
Nyní k Vašemu dalšímu tvrzení, a to že gravitační potenciál je veličina poměrová, nikoliv absolutní, takže pokud by hmotnost testovacího tělesa závisela na gravitačním potenciálu, mělo by toto těleso zároveň mnoho různých hmotností. Inu, opět prokazujete, že tu obecnou teorii relativity vůbec neznáte. Vycházíte totiž z vlastností Newtonova gravitačního potenciálu, ten má opravdu tu vlastnost, že k němu lze přičíst libovolně velkou konstantu, přičemž pohyb těles v těchto potenciálech bude v Newtonově teorii gravitace totožný, jinými slovy, ten potenciál není v Newtonově teorii gravitace jednoznačně určen. Jenže gravitace v Einsteinově obecné teorii relativity není Newtonova gravitace, mj. v žádném případě nemůže být popsána jediným potenciálem, tak jako je tomu v Newtonově gravitaci. V obecné teorii relativity je gravitace obecně popsána hned deseti složkami symetrického metrického tenzoru. Pouze ve velmi speciálních případech, jako jsou slabá gravitační pole a zároveň nerelativistické rychlosti těles, plus pokud navíc předpokládáme asymptoticky plochý prostoročas (protože předchozí dvě podmínky jde v principu splnit i v exoticky zakřivených prostoročasech, např. v prázdném vesmíru s vysokou křivostí), tak lze tyto složky metrického tenzoru vyjádřit s použitím jedné jediné funkce, která asymptoticky přechází v Newtonův gravitační potenciál. Teprve v tomto přiblížení potom můžeme přejít k tomu, že zanedbáme drobné křivosti prostoročasu a prostoročas budeme brát jako plochý, a veškerá působení metriky potom přepíšeme jako vliv Newtonovy gravitační síly. Teprve potom se nám objeví ta vlastnost, že k Newtonovu potenciálu můžeme libovolně přičíst konstantu, protože v Newtonově teorii gravitace se to opravdu neprojeví. Žádnou takovou konstantu ale nelze přičíst ke složkám metrického tenzoru v obecné relativitě, ani nikde uvnitř funkcí, pomocí kterých jsou ty složky metrického tenzoru vyjádřeny. Což si lze snadno ověřit např. při pohledu na Schwarzschildovu metriku viz první rovnice zde https://cs.wikipedia.org/wiki/Schwarzschildova_metrika , kde sice vidíme, že v ní formálně figuruje Newtonův potenciál GM/r, nicméně k tomuto potenciálu nelze žádnou konstantu přičíst, protože bychom tím dostali metriku, která už není řešením Einsteinových rovnic gravitačního pole pro statické sféricky symetrické těleso (jinými slovy bychom dostali nesmysl). Tedy to přičítání konstanty ke gravitačnímu potenciálu lze provádět v Newtonově teorii gravitace, nikoliv v obecné teorii relativity.
Pane Ouběchu, mám pro Vás návrh. V diskuzi zde https://www.osel.cz/11216-co-kolem-ceho-obiha-opravdu-a-snad-i-skutecne.html jste vzpomenul pana profesora Petra Kulhánka, nabyl jsem dojmu, že ho osobně znáte, pokud jde o dojem mylný, tak se omlouvám. Pokud ho ale opravdu znáte, zkuste ho požádat, jestli by nebyl tak ochotný a k těm Vašim omylům zde se nevyjádřil. Oni by si totiž i jiní čtenáři, kteří nejsou fyziky, rádi udělali obrázek, jak to teda je. Pan profesor by bezesporu byl velice překvapen nad tvrzeními, která zde šíříte.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-11 19:54:22
No ano, je to asi nedostatek mé představivosti. Nenapadlo mi, že v jedné neinerciální soustavě může být víc nesoumístných objektů, jeden z nich pozorovatel. Takže máte pravdu, dilatace času UVNITŘ neinerciálních soustav je. Jak jste napsal, není při pohledu z inerciální soustavy.
Pokud jde o hmotnosti v různém gravitačním potenciálu, jejich změna se rozhodně netýká vlastní hmotnosti (pozorovatele). Bohužel jsem to v textu zmínil jen jednou, víc jsem psal o hmotnosti klidové. Ale to nestačí.
Že má metrický tenzor více - díky symetrii 10 - složek, to není podstatné. Podstatné je, že neznáme homogenní gravitační pole. V něm by - i podle OTR - byl gravitační potenciál stejně relativní (určený až na libovolnou konstantu) jako v teorii Newtonově. Nejen to, mohly bychom zavést globální inerciální soustavu. - Ale dokáži si dost dobře představit reálné fyzikální podmínky, za kterých je homogenní grav. pole možné.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-11 20:03:10
P.S.: Respektive nejen já si to umím představit. Pánové Lens, Thirring to uvnitř rotující duté kulové slupky dokonce z OTR spočítali.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-11 20:48:53
Pane Ouběchu, opět píšete o věcech, které neznáte a kterým nerozumíte. Ani uvnitř rotující duté kulové slupky nemá gravitační pole libovůli v přičítání libovolné konstanty ke gravitačnímu potenciálu. Vnější pole rotující duté kulové slupky je dáno Kerrovou metrikou viz zde https://en.wikipedia.org/wiki/Kerr_metric , a vnitřní řešení je plně určeno podmínkami spojitosti pro přechod mezi slupkou a oblastí pod jejím vnitřním poloměrem. Žádná libovůle v přičítání aditivní konstanty zde není, ta metrika uvnitř slupky je rovnicemi OTR určená jednoznačně.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-11 22:10:13
Pane Broži, píšete o věcech, které neznáte a kterým očividně nerozumíte.
Uvnitř rotující hmotné kulové slupky (duté - jak jinak ?) je rotující Minkovského geometrie.
Mohu vám jen doporučit oprášit své znalosti relativity a nespat na letitých vavřínech.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-11 23:16:09
Pane Ouběchu, napsal jste cituji:
"Že má metrický tenzor více - díky symetrii 10 - složek, to není podstatné. Podstatné je, že neznáme homogenní gravitační pole. V něm by - i podle OTR - byl gravitační potenciál stejně relativní (určený až na libovolnou konstantu) jako v teorii Newtonově. Nejen to, mohly bychom zavést globální inerciální soustavu. - Ale dokáži si dost dobře představit reálné fyzikální podmínky, za kterých je homogenní grav. pole možné."
a dodal jste cituji:
"Respektive nejen já si to umím představit. Pánové Lens, Thirring to uvnitř rotující duté kulové slupky dokonce z OTR spočítali."
Nyní píšete:
„Uvnitř rotující hmotné kulové slupky (duté - jak jinak ?) je rotující Minkovského geometrie.“
Takže nyní Vám stačí ukázat, jak je ta rotující Minkowského geometrie coby řešení OTR pro vnitřek rotující slupky určená až na aditivní konstantu jako v teorii Newtonově. V Newtonově teorii je gravitační potenciál opravdu určen až na aditivní konstantu, o tom není pochyb, ale to platí v Newtonově teorie, ne v OTR. Vy teď máte možnost dokázat svá tvrzení a ukázat, kde se ta aditivní konstanta dá přičíst v řešení OTR popisující vnitřek té kulové slupky, tak, abychom stále měli platné řešení OTR pro daný problém. Moc se těším co z Vás vypadne, předpokládám, že to se to zase budete snažit zamluvit jinými svými výroky, jako v diskuzi zde https://www.osel.cz/11216-co-kolem-ceho-obiha-opravdu-a-snad-i-skutecne.html#poradna_kotva (mimochodem, stále trváte na tom, že bez globální Lorentzovy symetrie se spin fotonu může změnit z 1 na 0, jako jste tvrdil v tamní diskuzi?)
Všimněte si, jak jsem Vám to zjednodušil, buďto ukážete kde se na řešení OTR pro ten případ dá aplikovat ta aditivní konstanta, anebo to nedokážete. Pokud to nedokážete, tak naopak ukážete, že tady pouze plácáte nesmysly a snažíte se předstírat znalosti, které nemáte, podobně jako s tou údajnou změnou spinu fotonu z 1 na 0 při absenci globální Lorentzovy symetrie.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Ouběch,2020-09-12 12:20:47
Nejprve - když jsme u toho, čeho jsem si všiml, tak hlavně způsobu, jakým odvádíte pozornost od věcí, kde jste se zmýlil (ev. je dost neznáte), ale které jsou podstatné - přičemž z téhož viníte mne. Zajímavé.
Když se ale vrátím k meritu věci.
1) Uvnitř rotující hmotné kulové slupky je rotující Minkowského metrika. Nepočítal jsem to, ale o některých tvrzeních autorit (včetně toho, že to lze matematicky odvodit z OTR) v daném oboru nepochybuji. Hlavně v těch případech, kdy je to v souladu s logikou věci. Popřením této skutečnosti (Minkowského metriky uvnitř) jste se dopustil omylu.
2) Pokud je kdekoliv gravitační potenciál určený až na libovolnou konstantu, je velmi jednoduše možné, při splnění dalších podmínek, vynulovat působení gravitace, tedy přejít do Minkowského časoprostoru. Ty podmínky, za kterých je to možné jsou splněny právě uvnitř (rotující) kulové slupky.
3) Přestože je kvantová teorie pole založena na (lokálních) symetriích a další základní zákony fyziky jsou určeny (nelokálními) symetriemi, shoduji se a souhlasím se s mnoha autoritami, že úloha symetrií je ve fyzice zatím nedoceněna.
V konkrétním případě - Když nebude vesmír prostorově a časově homogenní, nebude se zachovávat hybnost a energie. Většinou se to interpretuje tak, že by se mohla hybnost nebo energie v určité třídě jevů nebo na určitých škálách nezachovávat a na ostatních ano. (Mluví se o energii, o hybnosti snad nikdo dnes už nepochybuje - i když byla doba, kdy se všeobecně tvrdilo, že se hybnost ve vertexech F. diagramů nezachovává. Nicméně myslím, že hybnost a energie jsou spojité nádoby - ale to jen na okraj, nikomu to nevnucuji.)
To je ale logická chyba. Kdyby nebylo těchto symetrií, nebyl by ani žádný důvod, aby se zákony zachování porušovaly jen někde nebo jen na některých škálách nebo jen málo. To by musela existovat jiná - neskonale složitější- symetrie, která by tyto specifické podmínky řídila. Ale o žádné takové nevíme.
No a obdobné je to s Lorentzovou symetrií a se spinem.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: černé díry
Pavel Brož,2020-09-12 14:11:21
Pane Ouběchu, nečekal jsem nic jiného než opět Vaše mlžení a překrucování, takže mě Vaše odpověď nepřekvapila.
Takže ad Váš bod 1, nikde jsem nepopíral, že uvnitř rotující hmotné kulové slupky je rotující Minkowského metrika. Ptal jsem se jak je ta rotující Minkowského geometrie coby řešení OTR pro vnitřek rotující slupky určená až na aditivní konstantu jako v teorii Newtonově. Já to řešení znám. Takže máte tam tu rotující Minkowského metriku, ta je řešením OTR pro vnitřek té slupky, a nyní na tuto metriku aplikujte tu aditivní konstantu, což podle Vás i v OTR jde. Jenže v OTR to ve skutečnosti nejde, což Vy nevíte.
Ad Váš bod 2, deset gravitačních potenciálů h_ij má v OTR tento vztah k metrice: g_ij = eta_ij + h_ij, kde g_ij je metrický tenzor toho prostoročasu, eta_ij je Minkovského metrika a h_ij jsou ony gravitační potenciály. Pokud v nějaké části celkového řešení OTR přechází metrika na Minkowského metriku, což je případ např. vnitřku rotující kulové slupky, kde akorát ještě musíme přejít do rotující soustavy, tak je tato metrika určena jednoznačně. To slovo jednoznačně je klíčové. Takže pokud je v dané oblasti a soustavě metrika g_ij = eta_ij, tedy pokud je tam h_ij=0, nemůže tam být zároveň g_ij=eta_ij+const_ij, kde aspoň jedna z konstant const_ij je nenulová. V té rotující soustavě je h_ij=0, a neexistuje žádná libovůle, aby se kterýkoliv z deseti gravitačních potenciálů nahradil libovolnou nenulovou konstantou, a to ani potenciál h_tt, který v limitě malých rychlostí a slabých polí přechází do gravitačního potenciálu Newtonovy teorie. Gravitační potenciály v OTR nemají tu libovůli, jakou má ten Newtonův gravitační potenciál, nelze k žádnému z nich přičíst libovolnou konstantu, jako to lze v Newtonově gravitaci, a to protože rovnice OTR jsou rovnicemi nelineárními, zatímco rovnice popisující v Newtonově teorii Newtonův gravitační potenciál je rovnice lineární. Tzn. že pouze v té limitě, kdy v rovnicích OTR zanedbáme všechny nelinearity a získáme rovnici Newtonovy gravitace, objeví se tam ta libovůle přičítat konstantu ke gravitačnímu potenciálu, ale tato libovůle v OTR není. Což díky Vašim neznalostem samozřejmě nevíte.
Ad Váš bod 3, tam jste si rozepsal filosofickou etudu, kterou končíte myšlenkovým skokem „No a podobné je to s Lorentzovou symetrií a spinem“, zřejmě ve snaze obhájit Vámi dříve vyřčený nesmysl, že bez globální Lorentzovy symetrie se spin fotonu může změnit z 1 na 0. Inu nemůže, globální Lorentzova symetrie v našem vesmíru přítomna není, a spin fotonů se opravdu nemění z 1 na 0, prostě proto, že jednotkovost spinu fotonu plyne z toho, že elektromagnetické pole je polem vektorovým, nikoliv skalárním, takže nemůže mít spin 0. S existencí globální Lorentzovy symetrie tato vlastnost nijak nesouvisí.
Takže pane Ouběchu, jste pouze diskuzní troll šířící naprosto nesmyslná tvrzení v oboru, ve kterém máte flagrantní neznalosti, sice vzdělanější než jiný diskuzní troll pan Jozef Navrátil, nicméně nesmysly Vámi zde šířené jsou v mnoha ohledech srovnatelné s nesmysly šířenými panem Navrátilem alias paní Šustovou.
gravitační vlny
Milan Bačík,2020-09-04 00:50:23
Zajímalo by mě, zda energie, která se proměnila na gravitační vlny se múže nějakým zpúsobem změnit opět na jiný druh energie, nebo zda již navždy zústane v této podobě. A pak by mě zajímalo zda samotné gravitační vlny něco váží a zda se s nimi počítá při hledání temné hmoty nebo energie.
Re: gravitační vlny
Vladimír Wagner,2020-09-04 10:52:27
Že to jde, je vidět, že jí můžeme detekovat. Při detekci se část energie z gravitačních vln transformuje na jiné druhy energie ve hmotě tohoto detektoru. Na druhé straně pravděpodobnost interakce gravitačních vln je extrémně malá. Proto k této transformaci energie z gravitačních vln na jinou formu energie dochází v zanedbatelném množství. Z hlediska stáří vesmíru je tak jejich existence téměř nekonečná. Je však třeba říci, že hustota toku gravitačních vln (v případě jejich existence, počtu gravitonu) ze zdrojů hvězdných (jejich konečných stádií) je velmi malá oproti kosmologickým gravitačním vlnám (gravitonům). Je to podobné, jako srovnání záření hvězd a reliktního mikrovlnného záření nebo neutrin z kosmických zdrojů a reliktních neutrin.
Re: Re: gravitační vlny
Petr Slachta,2020-09-04 16:06:26
Ja si treba myslel, ze pokud se jedna o pravidelne zmeny samotneho prostorocasu (vlneni), tak se to snad ani neda povazovat za energii v tom smyslu jak se ji bezne chape.
Re: Re: Re: gravitační vlny
Vladimír Wagner,2020-09-04 17:58:58
Gravitační vlny odnášejí energii a také ji nesou a mohou ji předat. Pokud jsou správné základní představy o tom, že by měla existovat i kvantová teorie gravitace, tak energie gravitonu bude dána vlnovou délkou gravitačních vln. A graviton ji při interakci předá, jako každá jiná částice, třeba foton.
Re: Re: Re: gravitační vlny
Pavel Brož,2020-09-05 00:51:20
Jenom doplním Vladimíra, ta problematika energie gravitačních vln, potažmo energie gravitačního pole, je v obecné teorii relativity docela složité téma, tento můj příspěvek je pouze náčrtkem tohoto problému, přičemž samozřejmě není možné v rozumném rozsahu obsáhnout všechny jeho důležité aspekty, byly o něm totiž napsány tisíce odborných prací.
Základním rozdílem mezi energií gravitačního pole a energií polí ostatních interakcí, jako je interakce elektromagnetická, slabá nebo silná, je v tom, že energie gravitačního pole není lokalizovatelná, zatímco energie těch ostatních polí lokalizovatelná je. Souvisí to s tím, jak v obecné teorii relativity popisujeme účinky gravitačního pole. Obecná teorie relativity je totiž postavená na tzv. principu ekvivalence, podle kterého je účinek gravitačního pole lokálně nerozlišitelný od účinku zrychlení. Tzn. že když stojíme na povrchu Země, působí na nás tíhové zrychlení g=9,81 ms^-2, a podle principu ekvivalence zde všechny fyzikální zákony probíhají lokálně stejně, jako by probíhaly v mezihvězdném prostoru uvnitř rakety, kterou by motory urychlovaly stejným zrychlením 9,81 ms^-2. Slovo lokálně je zde velice důležité, protože když v Česku i v Austrálii pustíme ve stejnou dobu těleso, budou se tato puštěná tělesa vůči sobě navzájem pohybovat se zrychlením 2g=19,62 ms^-2, a to se nám v té raketě nijak nepodaří napodobit. Pokud se ale omezíme na lokální děje, tak podle principu ekvivalence budou v té raketě probíhat naprosto identicky, jako zde na povrchu Země. Důsledkem principu ekvivalence je i známý fakt, že účinek gravitačního pole můžeme lokálně vynulovat přechodem do volně padající soustavy, např. volně padajícího výtahu, ale může to být třeba i orbitální stanice ISS, která vlastně při svém kruhovém pohybu kolem Země stále volně padá v jejím gravitačním poli (podobně jako volně padá vodorovně vržený kámen, akorát že v tomto případě nikdy nedopadne, protože byl vržen dostatečně velkou rychlostí).
Princip ekvivalence má i další důsledky, např. že všechna tělesa musí v gravitačním poli padat se stejným zrychlením. Pokud by tomu tak totiž nebylo, nemohlo by platit, že účinek gravitačního pole můžeme lokálně napodobit zrychleným pohybem, protože pokud se vůči původně volně se vznášejícím tělesům uvnitř rakety začne tato raketa pohybovat zrychleně, tak samozřejmě se všechna začnou pohybovat se stejným zrychlením (se kterým nakonec dopadnou na vnitřní stěnu rakety). Proto nepřekvapí, že testy obecné teorie relativity spočívají i v neustále zpřesňovaném ověřování faktu, který jako prvý popsal už Galileo Galilei, tedy že tělesa nestejné hmotnosti padají se stejným zrychlením, což je dnes ověřeno s relativní přesností až deset na minus patnáctou.
A nyní k tomu podstatnému – energie negravitačních polí je popsána jako složka tzv. tenzoru energie hybnosti, který udává hustotu energie toho pole, dále hustotu toku energie, dále hustoty hybnosti a dále hustotu toku hybnosti. Nebudu se zde pouštět do popisování, co konkrétně tyto pojmy znamenají, to co je důležité, je to, že pokud je ten tenzor energie-hybnosti v daném bodě nenulový, je v tom bodě nenulový bez ohledu na to, jakou pozorovací soustavu používáme. Tato vlastnost plyne z té „tenzorovosti“ té veličiny pro negravitační pole, je to matematický důsledek toho, jak je ta veličina definovaná, nebudu zde zabíhat do detailů. Podstatné je to, jaký to má důsledek pro kvanta toho pole, tj. pro odpovídající částice. Podle kvantové teorie pole jsou totiž částice kvanty odpovídajících polí, tak např. foton je kvantum elektromagnetického pole, elektron či pozitron odpovídajícími kvanty spinorového pole popisujícího elektrony a pozitrony, gluon je kvantum pole silné interakce, atd.. Skutečnost, že je v nějakém bodě nenulová hustota energie nějakého pole, znamená, že v tomto bodě s nenulovou pravděpodobností můžeme to kvantum čili tu odpovídající částici nalézt. Její energie sice může záviset na tom, jakou soustavu použijeme - tak např. energie elektronu je nejnižší v jeho klidové soustavě, zatímco v jiných je vyšší, podobně energie fotonu závisí na výběru pohybové soustavy (zde je důležité vědět, že ale neexistuje fyzikálně přípustná soustava pohybující se rychlostí světla) – nicméně tato energie nemůže být vynulována přechodem do nějaké jiné soustavy. Pokud je tedy tenzor energie hybnosti v daném bodě nenulový, tak v žádné soustavě se nám nestane, že by pravděpodobnost nalezení částice byla v tom bodě pro tu soustavu nulová. Jinými slovy, pokud v nějaké soustavě částice v daném bodě je, byť jen s nějakou pravděpodobností, tak se nemůže stát, že v jiné soustavě ta částice v témž bodě není, tzn. nemůže se stát, že pouhou změnou soustavy ta částice v daném bodě zmizí.
Nyní to porovnejme s gravitačním polem. Gravitační pole lze lokálně vynulovat přechodem do volně padající soustavy. Matematicky tomu odpovídá skutečnost, že neexistuje žádný tenzor energie-hybnosti gravitačního pole, pokud by totiž existoval, tak by nenulová hodnota tohoto tenzoru v nějakém bodě nešla vynulovat přechodem do jiné soustavy, jenže gravitační pole přechodem do volně padající soustavy lokálně vynulovat lze. A s tím souvisí i důsledek, že pokud budeme mít v nějakém bodě graviton jakožto kvantum gravitačního pole, tak pouhou změnou pozorovací soustavy umíme docílit toho, že pozorováno z té nové soustavy tam ten graviton nebude. Prostě pouhou změnou soustavy docílíme toho, že nám ten graviton v daném bodě zmizí. A přechodem nazpět do původní soustavy se v tom bodě zase objeví.
Tato právě popsaná vlastnost je jedním z vícero problémů způsobujících to, proč pro kvantování gravitačního pole zcela selhávají osvědčené postupy, které nám umožnily vytvořit úspěšné kvantové verze ostatních, tj. negravitačních polí.
Pro gravitační pole tedy neexistuje tenzor, který by byl protějškem tenzoru energie-hybnosti negravitačních polí, dá se zkonstruovat pouze pseudotenzor energie-hybnosti gravitačního pole (navíc nejednoznačně, tj. dá se definovat celá řada vzájemně odlišných pseudotenzorů energie-hybnosti gravitačního pole), který má tu vlastnost, že se dá lokálně vynulovat. Nicméně skutečnost, že energii gravitačního pole nelze lokalizovat, neznamená, že by gravitační pole nemohlo měnit energii hmoty. Tak např. gravitační pole Země zcela určitě mění energii na ní padajících těles. Nicméně musíme mít také na mysli to, že v klidové soustavě těch padajících těles pozorovatel žádnou změnu energie toho tělesa nezaznamená. Stejně tak i gravitační vlna coby měnící se křivost prostoročasu mění pohybový stav těles okolo kterých prochází, nicméně i v tomto případě v klidové soustavě těch těles samotných k žádné změně nedochází.
I v tomto případě, tak jako v předešlých, je jádro pudla skryto v té lokálnosti. Přibližme si to na hypotetickém příkladu, kdy bychom kolem jednoho tělesa nechali procházet obří gravitační vlnu, jejíž vlnová délka by byla mnohem větší, než je rozměr tělesa. Pokud bychom se nacházeli v klidové soustavě toho tělesa, tak bychom lokálně nic nezaznamenali, i v té procházející vlně bychom stále byli v té volně padající soustavě. Zjistili bychom ale pozorováním vzdálených hvězd dalekohledem, že jejich obraz by se nám během průběhu té vlny zavlnil. Jenže to je nelokální efekt.
Nyní nechme naší laboratoří procházet gravitační vlnu s mnohem menší vlnovou délkou, než je rozměr naší laboratoře (dejme tomu, že laboratoř se volně vznáší v mezihvězdném prostoru). V tomto případě zjistíme, že během průchodu gravitační vlny se nám tělesa v laboratoři začnou k sobě navzájem střídavě přibližovat a oddalovat. Pokud by navíc při nezměněné vlnové délce byla ta gravitační vlna extrémně intenzivní, popraskala by nám např. velká křehká tělesa, např. čočka v dalekohledu atd.. Popraskala by proto, že v dostatečně hodně se měnící křivosti prostoru neexistuje stabilní krystalová struktura – malé odchylky od Euklidovské geometrie se dají absorbovat malými deformacemi té mřížky, nicméně při překročení kritické míry těch deformací to praskne. Prasknutí té pevné křehké struktury je opět příkladem toho, že přestože lze energii gravitačního pole lokálně vynulovat, globálně jeho působení vynulovat nelze. Prostě v okamžiku, kdy na daných měřítkách nelze zanedbat nelokální gravitační efekty (např. slapové efekty), tak potom už můžeme spolehlivě detekovat energii předávanou gravitačním polem. Lokálně to ale nelze. Tu energii lze nelokálně detekovat i jinak než pomocí praskání těles, i u slabých gravitačních vln, kdy nic nepraská, ji lze detekovat např. jako oscilace dvou dostatečně vzdálených těles, což je zrovna případ, jak se gravitační vlny detekují v LIGO, jak už výše zmínil Vladimír Wagner.
Opačný extrém nastává naopak na kosmologických škálách, kdy musíme vzít v potaz rozpínání vesmíru. V tomto případě máme velmi vzdálené galaxie, které se od sebe v důsledku rozpínání vesmíru vzdalují, navíc během toho jak vesmír stárne, čím dál rychleji – teď nemám na mysli efekt zrychleného rozpínání vesmíru, ale čistě jen to, že tím rozpínáním se od sebe ty galaxie dostávají během miliard let dále a dále, tedy do vzdáleností, na kterých probíhá rozpínání rychleji než na počátečních vzdálenostech. Hypoteticky bychom mohli to čím dál rychlejší vzdalování vzdálené galaxie považovat za projev toho, že gravitační pole celého vesmíru jí předává energii. Takováto konstrukce sice vždy udělat lze, nepřináší ale nic užitečného, protože gravitační energii na kosmologických škálách nelze v principu vůbec nijak převádět na energie jiných typů (v čemž je rozdíl oproti příkladům s praskajícími tělesy výše), pouze bychom tedy uměle zkonstruovali veličinu popisující gravitační energii vesmíru tak, aby kompenzovala to pozorované rozpínání. Rozpínání vesmíru přitom plyne přímo z Einsteinových rovnic gravitačního pole, řešení popisující rozpínající vesmír z nich dostaneme pokud hledáme kosmologické řešení vyhovující požadavkům homogenity a izotropie vesmíru na velkých škálách. Na kosmologických škálách se proto s konceptem energie gravitačního pole nepracuje, je tam zbytečný, protože dynamika vzdálených galaxií plyne sama z toho rozpínajícího se prostoru.
Zrazka 2 ciernych dier?
Peter Fidler,2020-09-03 17:03:48
Ja by som mal tiez jednu laicku otazku. Ako je vobec mozne, ze vieme pozorovat zrazku ciernych dier? Zo vsetkych pop.-naucnych knih, ktore som na tuto temu cital som bol pouceny, ze samotny pad cohokolvek (uz ani nehovoriac o dalsej CD) sa pre vzdialeneho pozorovatela v case spomaluje, spomaluje az prakticky a efektivne zamrzne tesne pred kontaktom s horizontom.
Viem si predstavit, ze gr. vlnenie sa vyzaruje uz pocas padu, pri nejakych zbesilych obehoch (napriek tomu pre nas z dialky spomalenych) obidvoch CD okolo seba, a teda nieco pozorovat mozeme. Ale k samotnej udalosti splynutia by pre nas malo dojst az v nekonecnej buducnosti, nie?
Bol by som velmi vdacny, keby mi toto niekto kompetentny pomohol objasnit.
Re: Zrazka 2 ciernych dier?
Vladimír Wagner,2020-09-03 18:30:42
Je to dáno tím, že při této události nepozoruje vnější pozorovatel žádné děje na horizontu černé díry nebo pod ním. Ať už se to týká horizontů splývajících černých děr nebo nově vytvořeného horizontu černé díry vzniklé splynutím. Jak správně píšete, i ty gravitační vlny vznikají při přibližování černých děr a narušení okolního prostoročasu splynutím. Nenesou informaci z pod horizontu.
Podobné je to s pozorováním záření hmoty dopadající na černou díru. Toto záření také vzniká nad horizontem. Vnější pozorovatel nevidí dopad hmoty na horizont a cestu pod něj.
Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-03 21:50:16
Dakujem za odpoved.
Je to potom tak, ze my principialne nie sme schopni nikdy pozorovat finalny produkt kolizie 2 CD - novu, vacsiu CD? Ak by to bolo hypoteticky mozne a tieto kolidujuce diery by sa dali nejako zobrazit, aj potom co LIGO a VIRGO spozoruju ich "splynutie", po namiereni dalekohladov by sme na hviezdnom pozadi videli 2 cierne gule tesne vedla seba? (Ak si odmyslime vselijake deformacie a bizarnosti...) Ak je to takto a nemylim sa, ako mame spravne chapat tvrdenie typu "z 2 povodnych ciernych dier o hmotnosti 30 a 40 vznikla nova o hmotnosti povedzme 60"? Ta nova, jedna CD predsa nikdy nebude pre nas existovat, stale to budu dve (aj ked asi menej hmotne, kedze cast svojej hmoty postracali gravitacnym vlnenim pri spiralovani k sebe) cierne diery..?
Ked to takto premyslim do dosledkov, vlastne ma zaraza, ako vobec mozeme hocijaku ciernu dieru vo vesmire pozorovat? Nemali by sme vidiet iba vesmir plny kompaktnych objektov, niektorych viac, niektorych menej tesne nad kritickou hranicou (ako sa postupne "zhora" blizia k svojmu horizontu, ale stale viac spomaluju)? Takyto objekt by dokonca mohol veselo ziarit a my by sme ho na nejakych dalekych radiovych vlnach mohli stale pozorovat (t.j. nie len akrecny disk v strede s tajomnou ciernou oblastou, ale aj priamo z tejto oblasti by k nam stale malo prichadzat ziarenie, predpokladam, ze uz len radiove...).
Re: Re: Re: Zrazka 2 ciernych dier?
Peter Somatz,2020-09-03 22:25:26
Ked sa 2 masivne telesa hmotnosti CD priblizuju k sebe po spirale, tak v casopriestore vznikaju gravitacne vlny - a to este ovela skor, ako sa dotknu ich horizonty udalosti. LIGO a VIRGO to detekuju a na zaklade signalu vedia urcit ake 2 objekty sa zlucili.
CD neemituje elmag ziarenie, takze ju priamo nikdy nemozme vidiet. Len krivi okoloiduce ziarenie - ktoreho sa vase zastavenie casu netyka.
Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-04 08:21:08
>> Ked sa 2 masivne telesa hmotnosti...
Ano, ja netvrdim nic ine, akurat ze v nasom vesmire (pre nas, lokalne) k ziadnemu kontaktu ploch horizontu udalosti 2 ciernych dier nikdy nepride, a to je vec, na ktoru poukazujem a na ktoru sa tu pana Wagnera (pripadne aj inych, fundovanych) pytam.
>> CD neemituje elmag ziarenie...
No samotna CD nie, ale zase, v nasom vesmire sa my nikdy nedockame vzniku CD (tolko teda tvrdi moja laicka hypoteza :) a ten kompaktny, kolabujuci ale v case zamrznuty objekt este nie je ciernou dierou, preto vyzaruje a to ziarenie by sme v principe mohli prijimat ako nejake radio vlny (?)
Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Somatz,2020-09-04 14:32:21
Povedal by som ze na "pozorovanie skutocnosti" treba pouzivat spravnu metodu. Metoda "pozerania sa pomocou svetla" jednoducho pri CD dava zle vysledky - a nase extrapolovanie danych vysledov nas moze viest k chybnym zaverom ze "dana udalost sa stala v nekonecnom case". Tu je spravna metoda detekcia gravitacnych vln, ktora nam povie kedy, mozno aj kde, a ake objekty sa zrazili. Je to podobne ako ked ide okolo Vas auto a jeho motor vydava zvuk o nejakej frekvenciu, avsak kvoli vlastnostiam vzduchu pocujete vyssi, alebo nizsi ton - cize pouzivate nespravnu metodu. Podobne pri vzdalujucej sa stihacke, ktora prekroci rychlost zvuku, mozte teoreticky nespravne extrapolovat, ze stihacka zrychlila na nekonecnu rychlost. (Toto je asi blbost - ale, len ako priklad.)
Ak hodite do CD nejaky predmet a zasvietite si nan, resp. predmet sam ziari, tak budete pozorovat zmensujuci sa uhlovy rozmer predmetu, nacervenavanie (zly vysledok - predmet v skutocnosti nemeni farbu) a nakoniec jeho zmiznutie. Ak si prehrate zaznam zo superrychlej kamery, mozno zistite, ze sa pad "akoby spomaloval" a na zaklade toho extrapolujete, ze prakticky by ste ho nikdy nemali vidiet padnut. Ale raz jednoducho musia prist posledne odrazene, resp. emitovane fotony svetla predmetu. CD nespokytuje zaseknute ziarenie, ako vecnu pamiatku kazdeho predmetu, ktory do nej padol.
Re: Re: Re: Zrazka 2 ciernych dier?
Marek Fucila,2020-09-04 04:10:58
Zaujímavá úvaha. Ak si zoberieme, že horizont udalostí má tvar gule, potom pri splynutí dvoch čiernych dier by to pre nás mohlo zamrznúť v tvare dvoch prilepených gúľ. Ďalej by sa k sebe lepili ako nabité polystyrénové guličky, až bz supermasívna čierna diera mala tvar veľkej polystyrénovej gule (nezahladenej). Ak teda vznikla zlúčovaním čiernych dier.
Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-04 08:23:23
Ja by som si dovolil oponovat ze 2 ODDELENYCH gul (opat, pri zanedbanych deformaciach), ktore by sa k sebe limitne blizili, ale dotkli by sa az v pre nas nekonecne vzdialenej buducnosti.
Je vsak mozne a celkom pravdepodobne, ze sa s mojim laickym pohladom pochadzajucim mozno viac z klasickej fyziky mylim, a preto to sem pisem. Uz dlhsiu dobu ma trapia tieto myslienky.
Re: Re: Re: Zrazka 2 ciernych dier?
Vladimír Wagner,2020-09-04 11:04:33
To, že nemůže vnější pozorovatel pozorovat průchod objektu padajícího do černé díry skrze horizont událostí, neznamená, že nemůže vidět pohyb černých děr (pomocí signálů přicházejících z oblastí, které nejsou pod horizontem a nad ním. Také to neznamená, že by nemohl pozorovat splynutí černých děr a vytvoření nové černé díry. A to zase pomocí dějů probíhajících vně horizontu.
Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-04 11:25:12
No moment. Ja sa na nemoznost splynutia (z nasho pohladu, z dialky) 2 ciernych dier neodvolavam z toho dovodu, ze to nemozeme vidiet, ale ze efektivne (opat - pre nas, pozorujucich dianie z velkej vzdialenosti) k tomu splynutiu ani nedojde. Pre tie cierne diery lokalne ano, pre nas nie. Aspon tolko k tomu ako intuitivne chapem udalosti odohravajuce sa v blizkosti horizontu.
Ako mozem ja ako vzdialeny pozorovatel pozorovat efekty udalosti (splynutie 2 cd), ktore v mojom vesmire este nenastalo a nastane az v nekonecne vzdialenej buducnosti? To sa mi akosi nezda. Pozorovat predsa mozem iba udalosti (a nimi vyvolane nasledne udalosti) ktore sa uz odohrali, a teda v pripade ziarenia vychadzajuceho z oblasti nad horizontom priblizujucich sa dier musim stale pozorovat iba efekty neustale spomalovaneho priblizovania sa.
Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Vladimír Wagner,2020-09-04 12:08:52
Proč si myslíte, "ze efektivne (opat - pre nas, pozorujucich dianie z velkej vzdialenosti) k tomu splynutiu ani nedojde"? Z toho, že z pohledu vnějšího pozorovatele dojde k průchodu hmoty horizontem černé díry v nekonečném čase, nic takového neplyne. Stejně tak z toho neplyne, že vnější pozorovatel nepozoruje vznik a existenci černé díry.
Re: Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-04 12:39:51
Myslim si to preto, ze to je sposob ako som pochopil deje prebiehajuce v blizkosti horizontu pri pozorovani z velkej vzdialenosti. Vyplyvaju mi potom z toho napriklad taketo paradoxy a zatial som nenasiel nikoho fundovaneho, kto by mi to vysvetlil, preto som dufal, ze azda tu by som sa dockal :)
Ak teda jedno neplynie z druheho, ako ste napisali, mohli by ste mi to objasnit? Co z toho faktu teda plynie pre 2 priblizujuce sa cierne diery? Ak sa nam cela scena pri postupnom priblizovani sa 2 ciernych dier k sebe postupne v case zadrhava, ako mozem ja pozorovat vznik novej ciernej diery z dvoch povodnych? Ved toho sa predsa nikdy nedockam.
Re: Re: Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Vladimír Wagner,2020-09-04 14:14:49
Jak vypadá pozorování vzdáleného pozorovatele v elektromagnetickém oboru splynutí černých děr na pozadí bohaté hvězdné oblohy ukazuje následující simulace:
https://www.ligo.caltech.edu/video/ligo20160211v3
Vidíte, že žádné zaražení pohybu černých děr a splynutí horizontů do jednoho horizontu vzniklé černé díry nenastává. Simulace, jak to v tomto případě vypadá s vyzařováním gravitačních vln, je na následujícím videu:
https://youtu.be/_fjoVtATkkE
Samotné černé díry, jejich pohyb nebo jejich horizonty nezamrzají. To, že nevidíme pod horizont a že nemůžeme vidět průlet ničeho horizontem k tomu nevede.
Re: Re: Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Pavel Hudecek,2020-09-04 14:39:25
Když je někde paradox, znamená to, že něco důležitého bylo opomenuto. V případě pádu objektu do ČD:
(předpokládejme velkou ČD, aby u horizontu nebyly slapové jevy)
1. Padající kosmonaut pozoruje, že "normálně zahučel pod horizont" a ještě k tomu se v průběhu volného půdu nic zvláštního nedělo.
2. Nekonečně vzdálený pozorovatel pozoruje, že kosmonaut se, v důsledku dilatace času, čím dál tím pomaleji blíží - lepí na horizont, až je z něj infinitezimálně tenká samolepka, v důsledku kontrakce délek, infinitezimálně připláclá na horizontu.
ad 2: To se vždycky velmi líbilo odpůrců ČD, hlasatelům teorie gravastaru, ale je dobré si uvědomit, že se jedná o úvahu typu fyzika ZŠ, tedy se zanedbáním všech vlivů kromě probíraného jevu a tak jsou tam nějaké dodatečné, často nereálné předpoklady. V tomto případě je dodatečný předpoklad infinitezimální zanedbatelnost padajícího objektu vůči ČD. Reálný padající objekt, obzvláště pak srovnatelná ČD, tento předpoklad nesplňuje.
Horizont je jakási ekvipotenciální plocha, kde je úniková rychlost rovna c. Její tvar tak závisí na rozložení hmoty v okolí. Padajícímu kosmonautovi tak vyjde vstříc a "pozře" ho ještě před teoreticky infinitezimálním přiblížením. Takže srážka ČD obnáší plynulé splynutí horizontů.
Alespoň tak jsem to vždycky chápal já, prosím p. Wagnera o odpověď, zda je to správně.
Re: Re: Re: Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Vladimír Wagner,2020-09-04 18:03:32
Děkuji za moc pěkné doplnění. Je třeba překonat úvahy podobné těm, které vedou k závěru, že Achilles nemůže dohnat želvu. A to je přesně ten případ.
Re: Re: Re: Re: Re: Re: Re: Re: Zrazka 2 ciernych dier?
Peter Fidler,2020-09-05 21:47:42
OK, to znie zaujimavo. Dakujem za odpoved.
Re: Zrazka 2 ciernych dier?
Zita Šustová,2020-09-09 09:07:54
Aj ja by som bol velmi vdacny keby mi niekto kompetentný pomohol objasnit ( skvor jako do 40 rokov ) zda Hubbleho rozpínání vesmíru axiálně ( vedoucí do jednoho singulárního bodu – velkého třesku, vzniku z Ničeho ) není jinak, zda to nemůže být r o z b a l o v á n í čp, rozbalovávání křivostí dimenzí vesmíru a tím pádem těch singularit bude nekonečně mnoho, budou všude kolem nás na planckových délkách, a tedy v celém vesmíru se čp rozbaluje z každého bodu čp postupně do velkoškálových rozměrů.
Re: Re: Zrazka 2 ciernych dier?
,2020-09-11 07:22:10
Pozor na nick Zita Šustová - jedna sa o nelieceneho psychopata a stalkera Josefa Navratila. Tento tazky schizofrenik je posadnuty svojou retardovanou hypotezou kde 1+1=0 a kazdeho, kto poukaze na jeho skolacke chyby v matematike, je schopny zazalovat a posielat na neho udavacske dopisy domov a do prace. Tento uchylny paranoik je taktiez byvaly spolupracovnik STB.
Četnost srážek
Bohumil S.,2020-09-03 09:36:05
Dobrý den, děkuji za čtivý přehled posledních výsledků z LIGO + VIRGO.
Jako úplného laika mě překvapuje ta četnost srážek detekovaných pomocí LIGO + VIRGO. Kdysi jsem četl popularizační článek, kde byla kalkulace, jak moc je pravděpodobné, že se Slunce střetne s nějakou další hvězdou v Mléčné dráze. Kalkulace počítala s newtonovskou fyzikou, geometrickým rozměrem hvězd a jejich rychlostí. Pravděpodobnost, že Slunce překříží dráhu nějaké jiné hvězdy autoři spočítali na 6x10^11. Zároveň by načasování muselo být tak "nešťastné", že obě hvězdy dorazí do bodu křížení drah ve stejnou chvíli. Pravděpodobnost takové situace je ještě o dalších mnoho řádů nižší. Na základě výpočtu z článku lze odvodit, že nejen srážka Slunce s nějakou jinou hvězdou, nýbrž srážka jakýchkoliv dvou hvězd náhodně se potulujících Mléčnou dráhou je dost nepravděpodobná.
V souvislosti s černými děrami mám tyto předpoklady a otázky:
1.) Uvažovatelný geometrický rozměr ČD je mnohem menší než u hvězdy. Pravděpodobnost srážky náhodně se potulujících ČD je proto o dalších několik řádů nižší.
2.) Ve vesmíru je mnohem více běžných hvězd než černých děr. Pravděpodobnost srážky dvou ČD je proto mnohem nižší než pravděpodobnost srážky dvou hvězd.
3.) Černé díry se nemusejí nacházet přímo na kolizních drahách. O přiblížení se postará zpomalování způsobené vyzařováním gravitačních vln. To hraje ve prospěch četnosti srážek. Ale jak moc?
4.) Jestliže je možné, aby v binárních systémech ČD "spadly do sebe", stává se to i běžným dvojhvězdám? Předpokládám, že statisticky to musí být o několik řádů pravděpodobnější než splynutí dvou ČD v binárním systému.
5.) Předpokládá se snad, že ve vzdáleném vesmíru je hustota kosmických těles včetně ČD v prostoru o mnoho řádů vyšší, než co známe z Mléčné dráhy?
6.) Jsou nějaké další faktory, které mohou dostat ČD na kolikzní dráhy?
Jako úplný laik bych si myslel, že srážky dvou ČD budou v celém pozorovatelném vesmíru naprosto raritními událostmi. Na základě výsledků z LIGO + VIRGO mám ale spíš dojem, že k nim dochází prakticky každý pozemský den (máme omezené detekční možnosti, takže reálný počet srážek může být aspoň o řád vyšší). Dokáže se někdo znalejší vyjádřit k některým mým připomínkám a otázkám? Předem díky.
P.S.
Výpočet o pravděpodobnosti srážky Slunce pochází z knihy 220 záludných otázek z astronomie.
Re: Četnost srážek
Bohumil S.,2020-09-03 09:43:12
Ještě oprava: U toho čísla 6x10^11 nejde samozřejmě o pravděpodobnost, ale o průměrnou dobu vyjádřenou v pozemských letech, za kterou by k nějakému překřížení mělo statisticky dojít.
Re: Četnost srážek
Vladimír Wagner,2020-09-03 10:00:59
To je velice dobrý dotaz a téma. A jeden z nejdůležitějších cílů a významu pozorování gravitačních teleskopů je právě statistika různých typů událostí a hmotnosti černých děr. Dovolil bych si k tomu zatím pár poznámek:
1) Všechny pozorovaná i předpokládaná splynutí probíhají ve vázaném systému (tedy dominantně dvojhvězda složená z kompaktních konečných stádií).
2) Už pozorování dvojhvězd s kompaktní složkou a tím více binárních pulzarů a jejich četností bylo tak trochu překvapením. Nečekalo se, že výbuch supernovy přežije dvojhvězda ve vázaném stavu.
3) Splynutí dvou černých hvězd se nerealizuje srážkou volných černých děr, ale splynutím dvojhvězdy ze dvou černých děr, které ztrácejí energii postupně vyzařováním gravitačních vln.
4) Vázání volných černých děr do vázaného binárního systému je docela problém. Nestačí k tomu dvě tělesa, ale musí jich být více. Takže se předpokládá, že tyto dvojhvězdné systémy s černých děr jsou v takových oblastech galaxií, kde jsou vysoké hustoty hvězd a tedy i černých děr. Třeba právě zmiňované nitro kulových hvězdokup, nebo jádro galaxie.
Re: Re: Četnost srážek
Bohumil S.,2020-09-03 22:19:04
Děkuji za odpovědi. Ještě by mě tedy zajímalo, jak významné je vyzařování gravitačních vln u běžných dvojhvězd. Je možné, aby se k sobě vlivem vyzařování postupně přiblížily a nakonec splynuly? Případně v jakém časovém horizontu? Nebo je to tak, že dvojhvězdy sice gravitační vlny nezanedbatelně vyzařují, ale tlak vyzařovaných částic (slunečního-hvězdného větru) působí proti jejich přiblížení?
Re: Re: Re: Četnost srážek
Pavel Brož,2020-09-04 00:18:45
Pro běžné dvojhvězdy je vyzařování gravitačních vln zanedbatelné. Vzoreček najdete např zde https://en.wikipedia.org/wiki/Gravitational_wave#Binaries . Pro dvě hvězdy hmotnosti Slunce (tj. každá 2*10^30 kg) ve vzdálenosti 10 jeho průměrů (tj. ve vzdálenosti 10 miliónů kilometrů) vyjde něco přes tři bilióny let, tj. více než dvěstěkrát delší čas, než je stáří vesmíru. Ve skutečnosti nad efektem způsobeným vyzařováním gravitačních vln mohou často převážit jiné efekty. Tak např. Měsíc se od Země dlouhodobě vzdaluje, ačkoliv soustava Země-Měsíc samozřejmě také ztrácí energii vyzařováním gravitačních vln. Důvod je ten, že toto vzdalování jde na vrub zpomalování rotace Země, kdy Země je díky slapovým silám deformována, a protože rotuje rychleji než jakou rychlostí kolem ní obíhá Měsíc, tyto lokální deformace předbíhají Měsíc a tím ho urychlují ve směru jeho pohybu a v důsledku tím i posunují na vyšší a vyšší dráhu.
Naopak u velice kompaktních objektů typu neutronové hvězdy je ta ztráta energie vyzařováním velice podstatná a dokonce i pozorovatelná, viz rozpad dráhy Hulse-Taylorova binárního pulsaru zde https://en.wikipedia.org/wiki/Hulse%E2%80%93Taylor_binary .
Re: Četnost srážek
Pavel Nedbal,2020-09-05 14:05:49
Máte v podstatě pravdu.
Vzájemné pohlcení ČD je možné jen tehdy, když kolem sebe obíhají dvě, vzniklé postupným hvězdným vývojem, v malé vzdálenosti, aby doba vyzáření gravitační energie nepřekročila stáří vesmíru. To může být tak, že ve stadiu obra druhá složka, již zhroucená, spiráluje, ale ještě před sloučením ta okolo které obíhá, bouchne jako supernova (a neodstřelí ten kompakt). Jiný mechanismus na blízké oběhy si nelze představit.
Pak obdržíme to sloučení ČD, které aparatury sledují.
Ale další možné slučování je prakticky nemožné, jak již zmíněno, náhodná setkání vedoucí k přímé srážce =0, připojení pomocí třetího tělesa velmi nepravděpodobné, zejména, mělo -li by dojít k těsnému připojení (ta třetí složka by musela odnést nepředstavitelnou energii.
Takže soudím, že geneze středně - i velmi - masivních ČD musí probíhat jinými mechanismy, jako třeba akrecí v husté mlhovině, nebo jsou to objekty ze samých začátků, kdy se velmi hustá oblast zhroutila přímo.
Re: Re: Četnost srážek
Bohumil S.,2020-09-05 22:47:57
Děkuji za odpověďi Vám i panu Brožovi výše.
Ta poslední zmíněná možnost - zhroucení v době velmi mladého vesmíru jitří moji fantazii. Znamenalo by to, že vůbec nemusíme mít tušit kolik a jak velkých primordiálních děr se může vesmírem potulovat. Akrece z mlhoviny se ale zdá být přirozenějším vysvětlením vzniku masivních ČD.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



