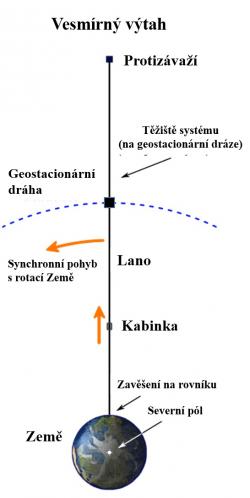
První návrh takového zařízení, a v tomto případě se jednalo právě o kosmickou věž sahající z povrchu Země do vesmíru, pochází od Konstantina Ciolkovského z roku 1895. V roce 1959 navrhl leningradský inženýr Jurij N. Arcutanov koncept klasického kosmického výtahu. Ten vznikne rozvinutím dlouhého lana z družice na geostacionární dráze ve výšce 35 800 km, která zdánlivě visí nad jedním místem na rovníku. Jedna část lana je z geostacionární dráhy až na zemský povrch. Druhá míří opačným směrem a musí být delší. Pokud jsou obě části správně nastavené, vyrovnává rostoucí gravitační sílu na konec blížící se k zemskému povrchu rostoucí odstředivá síla působící na konec, který se od Země vzdaluje. V konečné konfiguraci silnější přitažlivá síla na konci lana visícího nad povrchem Země je vyrovnána větší odstředivou silou na konci za geostacionární dráhou. Při ukotvení konce u povrchu Země na rovníku a přesně nastaveném směru a délce lana za geostacionární dráhu by se dosáhlo, že celý systém má těžiště na geostacionární dráze, bude obíhat okolo Země za jeden den ve shodě s její rotací a bude tak viset nad příslušným místem ukotvení na rovníku. Inženýr Arcutan doporučoval i postupné zužování lan, aby se se v něm nezvyšovalo napětí. Největší průřez by lana měla mít na geostacionární dráze. Článek o vesmírném výtahu publikoval v nedělní příloze sovětských novin Pravda 31. července 1960.
Jeho práce nebyla z pochopitelných důvodů na západě zaznamenána. Zde se idea o výtahu vytvořeném tenkými lany, které by se odvíjely opačným směrem z družice na geostacionární dráze, poprvé nezávisle objevila v roce 1966 v článku skupiny amerických oceánografů pod vedením Johna D. Isaacse v časopise Science. Důvodem zájmů oceánografů bylo, že měli zkušenosti s dlouhými lany zatěžovanými vlastní vahou. Ovšem i tentokrát prozatím zapadla.
Do obecného povědomí dostal kosmický výtah Jerome Pearson, který pracoval pro výzkumné laboratoře NASA v rámci programu Apollo a od roku 1971 pro Air Force Research Laboratory. V roce 1975 publikoval v odborném časopise Acta Astronautica článek o vesmírném výtahu. Později navrhl i měsíční vesmírný výtah, který by využíval Lagrangeovy librační body soustavy Země a Měsíce.
S ním konzultoval Arthur C. Clark principy a technologie tohoto zařízení při psaní románu Rajské fontány, který je asi nejznámějším popisem vesmírného výtahu ve vědecké fantastice. Později se objevuje v řadě sci-fi děl, klíčovou roli hraje třeba v trilogii o kolonizaci Marsu Kim Stanley Robinsona Rudý Mars, Zelený Mars a Modrý Mars.
Základní schéma klasického vesmírného výtahu a klíčové problémy
Základní součástí klasického vesmírného výtahu je základna ve formě družice na geostacionární dráze ve vzdálenosti 35 800 km od povrchu Země, ze které se začnou v opačných směrech konstruovat lana. Jedno směrem k zemskému povrchu a druhé od něj pryč. K lanu je pak připojen systém, většinou na elektromagnetický pohon, který umožňuje pohyb kabinek po něm. Rozvinutý a dokončený výtah pak může pomocí kabinek velmi efektivně a s nízkými energetickými náklady dopravovat materiál i lidi ze zemského povrchu na různé orbity okolo Země.
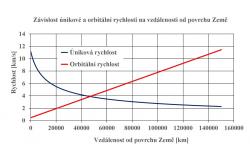
Úhlová rychlost pohybu okolo Země je u všech částí výtahu stejná. Orbitální rychlost pak závisí na vzdálenosti od jejího středu. Pokud jde o nízké oběžné dráhy, je potřeba, aby případný výtahem dopravovaný budoucí satelit uvolňovaný na vybrané oběžné dráze měl pohonné jednotky, které zvýší orbitální rychlost z velikosti menší než 3,1 km/s, která je na geostacionární oběžné dráze, na až 7,7 km/s, která je na drahách nejblíže k zemskému povrchu. V případě drah za tou geostacionární se orbitální rychlost musí zmenšit. Pokud dopravíme náklad po laně do vzdálenosti 47000 km od povrchu Země, umožníme mu opustit zemskou přitažlivost a vydat se na meziplanetární dráhu. V každém případě se náklad dostane na cestu k Měsíc a k planetám s menšími energetickými nároky. I když rovníková dráha není ideální start pro cestu k Měsíci či planetám. Vždy je pak potřeba změna roviny dráhy s příslušnými energetickými nároky.
Na vzdálenějším konci se doporučuje mít protiváhu o dostatečné hmotnosti, které umožňuje snížit délku této části lana. Jestliže lano k povrchu Země má délku 35 800 km, tak druhá část směrem od Země by měla mít větší délku, aby se odstředivé a gravitační síly správně kompenzovaly. Celková délka výtahu tak musí být zhruba 144 000 km. Ta se dá zkrátit právě pomocí protizávaží úměrně jeho hmotnosti. Jako protizávaží je možné využít různý vesmírný odpad z vyřazených družic, zařízení využívané pro výstavbu výtahu nebo zachycená planetka.
Samotná družicová základna na geostacionární dráze je gravitačním středem systému a musí mít navijáky, které umožňují manipulovat s délkou lan a udržovat systém v rovnováze a správné poloze. A bude kompenzovat i změny těžiště způsobené pohybem nákladů či některými vnějšími vlivy. Předpokládá se, že bude obsahovat také zařízení pro nakládku a vyložení kosmických lodí a další vybavení. Případně i obyvatelný prostor, možná v podobě rotující struktury s umělou gravitací.
Při cestě ze zemského povrchu na geostacionární dráhu a ještě dále se jedná o vzdálenosti v řádu desítek tisíc kilometrů, kabiny se tak musí pohybovat velmi rychle. Proto se uvažuje o elektromagnetickém pohonu a bezkontaktních systémech typu maglev, které umožňují v realitě rychlosti mnoha stovek a v principu i tisíců km/h. V tomto případě je možné také část energie spotřebované na urychlení kabiny získat zpět při jejím brždění. Podle odhadů má mít doprava nákladu na orbitu velmi nízké energetické nároky, něco okolo 14,8 kWh/kg.
Superpevné materiály pro lana
Základním problémem je získání dostatečně pevného a lehkého materiálu pro lano. Čím těžší materiál je, tím větší síly vznikají. Zároveň musí lano vydržet obrovské namáhání. Naděje se v tomto případě upínají ke grafenovým nanotrubičkám, případně k nanotrubičkám z nitridu bóru či diamantovým vláknům. Dostatečně pevný a lehký materiál lana je tím nejkritičtějším místem projektu. Pevnost materiálu lze zhodnotit podle tržné délky lana, která udává, při jaké jeho délce by v gravitačním poli Země došlo k přetržení. Pro současné limitní materiály, jakými jsou kevlar nebo speciální plasty, je tržná délka mezi 100 až 300 km. Pro srovnání, pro kovy jako titan, ocel nebo hliník je to mezi 20 až 30 km, Zmíněné budoucí materiály z nanotrubiček například grafenu by mohly mít tržnou délku i 5000 až 6000 km.
Grafen je materiál z uhlíku, který se rád spojuje a vytváří i velice komplikované prostorové struktury. V daném případě se dají vytvářet destičky a nanotrubičky o tloušťkách v řádu rozměru atomu. V dané vrstvě jsou atomy uhlíku uspořádány do šestihranné mřížky. O podobné struktuře se uvažovalo a náznaky jednovrstevných struktur uhlíku byly zkoumány již v minulém století. Teprve v roce 2004 však poprvé vyrobili grafen ve větším množství dva fyzikové ruského původu Andre Geim a Konstantin Novoselov, kteří za tento objev dostali v roce 2010 Nobelovu cenu. Modul pružnosti je u něj extrémně velký, jako u diamantu, zároveň však je možné grafen roztáhnout o čtvrtinu jeho délky, jako je tomu třeba u gumy. Grafen je až zhruba 200 krát pevnější než nejpevnější ocel.
Výhodou grafenu jsou jeho různorodé elektrické vlastnosti. Lze jej připravit v podobě vodiče, polovodiče i nevodiče. Lze například využít toho, že na dlouhém lanu z vodivého materiálu, které se pohybuje v magnetickém poli Země, se generuje elektrické napětí a proud. Ještě více se tyto vlastnosti využijí v řadě aplikací v elektronice.
Postupně se zefektivňují metody výroby různých forem grafenu a zlepšují jejich vlastnosti. Dnes už se nanotrubičky produkují ve velkém množství a dobré kvalitě. Přesto je však výroba superpevných lan grafenu se zmiňovanou extrémní tržnou délkou zatím ještě daleko. Přiblížit by jej měl intenzivní výzkum vlastností grafenu a vývoj nových postupů při jeho výrobě. Různé metody umožňují v současné době vyrobit dvojrozměrný film o rozměrech několik centimetrů a atomární tloušťce.
Často se při jeho studiu a hodnocení kvality vyrobeného grafenu využívají i jaderně analytické metody a této oblasti se věnuje třeba i skupiny v Ústavu jaderné fyziky AV ČR.
Ke zlepšení mechanických vlastností by mohlo přispět dosažení optimální třírozměrné konfigurace dvojrozměrné struktury. Zatím jsme na této cestě na začátku. Při konstituování třírozměrné struktury s využitím dvourozměrných šupinek se využívá tlak a vysoké teploty. Dostávají se tak materiály se stále lepšími mechanickými vlastnostmi. Tovární produkce lan se stabilními a zaručenými vlastnostmi však ještě není možná. Další zlepšení by mohlo přinést zabudování grafenové struktury do niklové matrice nebo úplně nové typy materiálů.
Reálné testy dlouhých kabelů a lan ve vesmíru
Připravovala se řada projektů testů platforem vypouštěných z družic na různě dlouhých lanech. Používají se zatím klasické materiály, třeba zmíněný kevlar. Z nich několik se již podařilo s rozdílným stupněm úspěšnosti realizovat. Často byly zaměřeny na studium magnetického pole Země a toků částic. Další uvažované využití má blíže k vesmírnému výtahu. Jde o možnost odstraňování odpadu z ISS pomocí snížení jeho rychlosti a přesun na nižší oběžnou dráhu, kde je hustší atmosféra. Délka lana by v tomto případě byla 100 km. Na dlouhém laně by mohly viset i družice zkoumající atmosféru Země na velmi nízkých oběžných drahách, kde samostatné družice kvůli odporu zbytků atmosféry nemohou obíhat. Možné je také využití toků v plazmě ionosféry ke generování energie pro zajištění jemného manévrování a stabilizace vesmírných objektů. Stejně tak se dá využívat síla, která působí na vodič, v němž teče proud a zároveň se pohybuje v magnetickém poli Země.
Podívejme se na některé projekty podrobněji. Několik realizovala NASA ve spolupráci s dalšími výzkumnými institucemi a využíval se raketoplán nebo stanice ISS. Prvním větším experimentem byl projekt s Italskou vesmírnou agenturou TSS (Tethered Satellite System Mission). V jeho rámci se vypustily dvě sondy. Družice TSS-1 byla vynesena při letu raketoplánu Atlantis (STS-46) začátkem srpna 1992. Délka kabelu se satelitem na konci, která se měla odvinout, byla 20 000 m. Bohužel se však podařila rozvinout pouze 255 m. Pak se lano zaseklo. Experiment měl ukázat, jak se systém s dlouhým lanem chová v gravitačním poli Země a otestovat dynamické vlastnosti takové sestavy. Krátká délka lana neumožnila uskutečnit většinu testů s produkcí elektřiny pomocí vodivého lana. Generované napětí, proud a síly měly totiž příliš malou hodnotu.

Opakování experimentu se uskutečnilo o čtyři roky později v únoru 1996 při letu raketoplánu Columbie (STS-75). Při letu TSS-1R se podařilo rozvinout lano do délky 19,7 km. Tedy téměř úplně, protože celková délka byla 20,7 km. Pak došlo k poškození kabelu pravděpodobně zkratem v místě s poškozenou izolací a satelit se uvolnil. Přesto se ještě před odtržením satelitu podařilo uskutečnit řadu měření interakce magnetického pole a plazmy v okolí Země s takovou soustavou s dlouhým vodivým kabelem. Měření začala v době, kdy se odvinulo 6 km lana. Generovaná hodnota proudu byla 480 mA, což bylo 200krát více než v případě TSS-1.
V letech 1993 a 1994 proběhlo vypuštění tří sond v rámci projektu SEDS (Small Expendable Deployer System). Sondy SEDS I a SEDS II se uvolnily na laně délky 20 km z druhého stupně rakety Delta-II. V prvním případě se testovalo pouze rozvinutí lana a po jednom oběhu byla zátěž odpojena. V případě SEDS II došlo k odtržení po necelých čtyřech dnech po rozvinutí. U družice PMG (Plasma Motor Generator) mělo lano délku 500 metrů. Poprvé se tak ověřila práce systémů s kilometrovými lany, jejich mechanické i elektrodynamické vlastnosti. Právě družice PMG testovala produkci elektřiny.
V roce 1996 byla vypuštěna sestava TiPS (Tether Physics and Survivability Experiment), která se skládala ze dvou těles s označením Ralph a Norton propojených lanem o délce 4000 m. Experiment fungoval až do července 2006, kdy došlo k přetržení lana. Získal se značný soubor experimentálních dat o chování sestavy. Ukázalo se, že systém vydrží řadu let a že brzké odtržení v případě SEDS II bylo spíše nešťastnou událostí.
Japonský projekt KITE (Kounotori Integrated Tether Experiments) je zaměřen na využití vodivého kabelu pro generování elektřiny a síly pro systémy, které by čistily vesmírný prostor v okolí Země od větších kusů odpadu. Jeho úkolem je právě studium reálného elektrodynamické chování systému s dlouhým vodivým kabelem. Délka lana, na jejímž konci je těleso o hmotnosti 20 kg, se předpokládá 700 m. V tomto případě probíhá rozvinutí lana z přístrojové plošiny vypuštěné ze stanice ISS. Kounotori 6 byla dopravena na stanici ISS v prosinci 2016, samotné uvolňování plošiny proběhlo koncem ledna 2017. Rozvinout lano se však nepodařilo.
Je vidět, že prozatím se podařilo realizovat pouze první krůčky v testech lan. Ty jsou zatím velmi krátká a i zátěže na jejich konci jsou většinou velmi lehké. Částečné úspěchy však potvrzují předpoklady a naznačují, že technologie, které se mají využívat v případě vesmírného výtahu, jsou perspektivní a dosažitelné.
Pozemní stanice, případně věž do vesmíru
Velkou výzvou je i základna, kde by byl vesmírný výtah ukotven. Problémem jsou udržení stability celého systému a také způsoby, jak bude systém čelit katastrofickým jevům v atmosféře, jako jsou velké bouře, vichřice a další události. Zde je výhodou, že na rovníku, kde by měl vesmírný výtah končit, je takových katastrofický zvratů v počasí méně.
Jednou z možností je, že by základna na pozemském konci byla mobilní, například velké plavidlo umístěné v rovníkových částech oceánu. Další výhodou mobilního zařízení je, že se zjednoduší vyhýbání kosmickému smetí. Výhodnou polohou na pevnině by byl vysoký kopec.
Pozemní stanicí by mohla být i velmi vysoká věž. To by mohlo zjednodušit situaci s ukotvením lana i jeho ochranou a stabilitou, neprocházelo by hustými vrstvami atmosféry. O věžích, které by dosahovaly výšky až 20 km a tím až za hranice nejhustších vrstev atmosféry, se uvažuje i při ulehčení startu raket a snížení ceny vynesení nákladu do vesmíru. Připomeňme, že v současnosti je nejvyšší budovou na světě Burdž Chalífa v Dubaji s výškou 828 m. Ve výstavbě je Jeddah Tower v Saudské Arábii s výškou 1008 m. Z klasických materiálů dnes dokážeme v principu postavit budovu o výšce i několik kilometrů. Současné omezení výšky je dáno smysluplností velmi vysokých budov a ekonomickými důvody, nikoliv nemožností jejich postavení. Nové materiály a technologii by v budoucnu mohly umožnit stavět snadno budovy o výšce desítky i stovky kilometrů. V tomto případě je velmi důležitý poměr mezi základnou a výškou. I v současné době lze v principu vybudovat i extrémně vysoké budovy při dostatečně širokých základech.
V některých úvahách se předpokládá na několika takových věžích vybudovat půloblouk končící ve výšce 15 km. S využitím elektromagnetického pohonu maglev by se získala část potřebné rychlosti a nosič by se dopravil do výšky nad 83 % zemské atmosféry. Ulehčilo by se tak dosažení nízké oběžné dráhy okolo Země.
Pohon výtahu
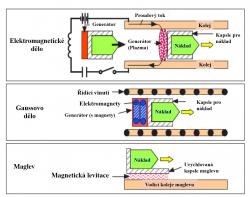
V principu lze i u vesmírného výtahu využít mechanického mechanismu pro vynášení nákladu, jako je mají výtahy klasické. Nevýhodou u nich je, že musí mít kola, koleje a možné jejich rychlosti jsou omezené. Proto se uvažuje o některém z elektromagnetických principů pohonu. Ten umožňuje bezdotykový pohyb kabiny a tím i velmi vysoké rychlosti. Vysoká rychlost je velmi důležitá u klasického vesmírného výtahu, kde je třeba překonat vzdálenosti v řádu tisíců kilometrů. Pro přepravu s menším zrychlením do 3 g se předpokládá využití systémů maglev, které jsou vhodné pro přepravu osob a křehkého nákladu. K mnohem rychlejší přepravě odolného nákladu by mohl sloužit systém elektromagnetického děla, kdy se dosahuje vysokých zrychlení. Výhodou elektromagnetického pohonu je i to, že část energie použité na urychlování kapsle lze opět získat při brždění.
Systémy typu maglev využívají levitaci na magnetickém polštáři vytvářeném nejčastěji supravodivými magnety zabudovanými v trati i ve vozidle. Pohon je zajištěný lineárními indukčními motory. V pozemské praxi se testuje a už i využívá pro rychlou dopravu, která by mohla postupně konkurovat letecké. JR-Maglev je provozován na zkušební trati v Japonsku a v Německu fungovalo podobné zařízení M-Bahn v letech 1984 až 1991. V reálném provozu je od roku 2004 německý systém Transrapid v Šanghaji. V provozu dosahuje 420 km/h, při testech přes 500 km/h a překonal i 600 km/h. Cesta na letiště dlouhá 30 km tak trvá celkově 8 minut. Druhý čínský maglev ve městě Changsha byl uveden do provozu v roce 2016. Jde o pomalý typ s rychlosti do 120 km/h. V Japonsku byl v rámci Světového Expa postaven relativně pomalý maglev Linimo. V roce 2016 začal v Jižní Koreji pracovat systém Incheon Airport Maglev, jehož operační rychlost je 110 km/h.
Maglev může dosahovat rychlostí až několik 1000 km/h v případě, že by se pohyboval v tunelu se sníženým tlakem vzduchu. Hlavním problémem je totiž aerodynamický odpor. Při využití tunelu by měl tento systém konkurovat letecké dopravě. Na stejném principu jako maglev může být založeno zařízení, které bude dopravovat náklad a lidi ne v horizontálním, ale vertikálním směru. Systém by umožňoval dopravu nákladu do velkých výšek až nad zemskou atmosféru. Zařízení nemusí mít příliš velké zrychlení, protože dráha pro urychlení je relativně dlouhá. V tomto případě by dosahované rychlosti mohly být i vyšší než u klasického maglevu. Na systému využívajícího elektromagnetický pohon dosahujícího rychlosti až 1000 km/h v tunelu se sníženým tlakem vzduchu pod názvem hyperloop pracuje i Elon Musk. Jeho společnost Hyperloop One dokončuje první testovací moduly a připravuje testovací dráhu.
Další možností, která by se dala využít v případě odolného nákladu, jsou systémy s intenzivním urychlováním. V tomto případě je zrychlení mnoho g a systém nelze použít pro přepravu lidí. Použil by se princip elektromagnetického děla (railgun), někdy označovaný jako kolejnicové elektromagnetické dělo. Další možností je Gaussovo dělo (coil gun), které se také označuje jako elektromagnetická puška nebo pulsní urychlovač feromagnetických projektilů. Zbraňová terminologie je v tomto případě využívána proto, že na konci urychlovacího systému má urychlované těleso rychlost srovnatelnou s rychlostí náboje opouštějícího ústí děla či pušky. V tomto případě se tak vracím k cestě na měsíc s využitím děla, které popsal ve své knize Jules Verne.
K urychlování se ovšem využívá elektromagnetické pole, takže v tomto směru je situace podobná urychlovači částic, jen urychlovaný objekt je o mnoho řádů těžší. Elektromagnetické dělo využívá Lorentzovy síly, která působí na pohybující se náboj a tedy i vodič, ve kterém teče proud, v případě, že jsou umístěny v magnetickém poli. Velký proud v jednotlivých kolejnicích hlavně elektromagnetického děla teče opačným směrem a mezi nimi se vytváří téměř homogenní magnetické pole, které intenzivní Lorentzovou silou působí na proud tekoucí v plazmě od jedné kolejnice ke druhé. Plazma pak žene urychlovaný objekt. V případě Gaussova děla je střela z magnetického materiálu urychlována elektromagnetickou indukcí pomocí elektromagnetických cívek.
V poslední době nastal v této oblasti hlavně díky zájmu americké armády značný rozvoj. Ta má zájem využívat děla na tomto principu k vystřelování nábojů s extrémními rychlostmi, takže by prorážely pancíře a ničily díky své vysoké rychlosti a kinetické energii. Při testech s elektromagnetickým dělem dosahují vystřelené náboje běžně rychlosti přes 6 000 km/h, podařilo se překonat hranici 7000 km/h, to už je téměř 2 km/s, a dosáhnout pro náboj o hmotnosti 3,2 kg i rychlosti 9000 km/h, což je 2,5 km/s. A například úniková rychlost z povrchu Měsíce je jen 2,36 km/s. Taková elektromagnetická děla by se tak v principu dala využívat k dopravě materiálu z povrchu Měsíce do kosmu. Menší hmotnosti už současné technologie dokáží urychlit i na vyšší rychlosti a v budoucnu jsou v principu dosažitelné i rychlosti 10 km/s.

Základní problémy, na které se naráží, je velmi vysoké mechanické a tepelné namáhání kolejnic. Působí na ně elektrický oblouk a jeho plazma vytvořené tokem proudu mezi kolejnicemi. Zároveň také urychlovaný náboj, který už v hlavni dosahuje extrémních rychlostí. Elektromagnetické dělo potřebuje velmi vysoký výkon. To je důvod, proč se v prototypových verzích objevuje až v posledních letech a jeho zavedení do výzbroje se teprve připravuje a je možné pouze na lodích s jaderné zdroje energie, které jsou schopné zajistit dostatečný elektrický výkon. Větší kapsle, které budou potřeba u vesmírného výtahu, budou klást ještě vyšší nároky.
Provoz přepravního systému vesmírného výtahu tak bude mít značné nároky na elektrický výkon. Nejjednodušším zdrojem elektřiny by mohly být fotovoltaické panely. Lano kosmického výtahu by se dalo využít i pro dopravu elektřiny vyrobené velkými fotovoltaickými elektrárnami na oběžné dráze na zemský povrch. Další možností získání dodatečného zdroje elektřiny je využití plazmy v okolí Země a pohybu dlouhých vodičů v magnetické poli Země.
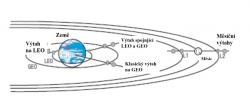
Výtah mezi různými oběžnými drahami
Kromě klasického vesmírného výtahu využívajícího základnu na geostacionární dráze existují i jednodušší varianty těchto zařízení. Menší typ vesmírného výtahu může spojovat oblast těsně nad hranicemi hustších vrstev atmosféry a relativně nízké oběžné dráhy. V tomto případě je centrální stanice a gravitační střed systému na relativně nízké oběžné dráze. Od něj by pak vybíhalo jedno lano směrem k zemskému povrchu a jedno směrem opačným.
Při využití přepravy nákladu zachyceného koncem lana blízko povrchu Země se sníží orbitální rychlost, kterou je potřeba udělit tělesu při vypouštění. Takový výtah by se v principu mohl vybudovat už s využitím současných materiálů jen s pomocí rozšiřování tloušťky lana směrem k družicové základně. Výtah by pravidelně prolétal nad daným místem a zde by k němu byl ze zemského povrchu vypouštěn náklad. Byl by zachycen a přepraven na druhý konec výtahu. V tomto případě lze spojit využití vystřelování nákladu pomocí elektromagnetického děla a jeho přenesení na vyšší orbitu pomocí vesmírného výtahu.
Měsíční i marsovský výtah
Pro lehčí tělesa ve Sluneční soustavě, jako je například Měsíc, nemusí být lano až tak pevné a požadované vlastnosti už mají současné materiály. Jde například o kevlar s hustotu 1440 kg/m3. Měsíc je navíc velmi blízko Země. Pokud suroviny z něj budou uplatnitelné ve vesmíru, tak je jejich velmi přirozeným zdrojem. Je tak možné, že měsíční vesmírný výtah předběhne ten pozemský. Na druhé straně máme ovšem pro dopravu materiálů z měsíčního povrchu více konkurujících možností. Už bylo zmíněno elektromagnetické dělo, u něhož se už nyní daří dosahovat potřebných rychlostí projektilů a s výhodou se využije toho, že na Měsíci je vakuum.
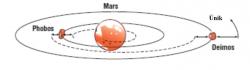
Dalším tělesem, u kterého se nejen ve sci-fi uvažuje o vesmírném výtahu, je Mars. Zde je opět nejzajímavější výtah za základnou na synchronní dráze, tentokrát na aresynchronní. Takový je například popsán právě v cyklu Kim Staleye Robinsona o kolonizaci Marsu.
Další možností by byly kratší nesynchronní výtahy, jejichž základny by byly na měsících Marsu Phobosu a Deimosu. Ty by umožňovaly postupný efektivní přesun nákladu mezi různými orbitálními drahami okolo Marsu a nakonec doprava mezi povrchem Marsu a různými orbitami kolem něj.
Některá rizika a jak jim čelit
První možnost ohrožení se týká pozemní základny a vlivu katastrofických jevů vznikajících při prudkých změnách počasí, zemětřeseních nebo vlnách cunami. Z tohoto hlediska je výhodou to, že pro kosmický výtah je důležité mít pozemní stanici na rovníku. Rovník je totiž z hlediska povětrnostních výkyvů a dramatických událostí spíše stabilnější. Oceánské rovníkové proudy se většinou pohybují z východu na západ, kromě výjimky těsně u povrchu, kde protéká teplý rovníkový protiproud, který teče od západu na východ.
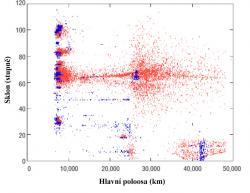
V rovníkových oblastech je i rychlost větrného proudění nižší a stabilnější. Teploty se tam také nemění v příliš velkém rozsahu. Pochopitelně, že mrazivé počasí a ledové krystalky či pokryv jsou i zde možné ve výškách 4 až 5 km. Konstrukce tak na to musí být připravena. Postupnou degradaci materiálů může způsobit atomární kyslík, ionosférické plazma, nabité částice v různých vzdálenostech od Země a také ultrafialové záření. Je však třeba připomenout, že s tímto jsme se dokázali vypořádat u řady současných družic a vesmírných sond. Vesmírný výtah by měl fungovat velmi dlouhou dobu, takže je potřeba počítat s jeho údržbou.
Jedním z největších rizik je kosmické smetí na oběžných drahách okolo Země a meteority. S rostoucí intenzitou využívání družic Země přibývá hlavně na nižších oběžných drahách velký počet menších i větších těles. V současné době se sleduje téměř deset tisíc objektů větších než 10 cm. Z nich je pouze něco mezi 300 až 400 fungujících zařízení. Zbytek jsou nefungující družice, zbytky nosných zařízení a pozůstatky různých srážek.
Malých kousků materiálů s průměrem menším než 1 mm je nespočetně. Mohou však způsobovat pouze postupnou erozi povrchu různých částí zařízení. Již zmíněná tělesa z rozměrem nad 10 cm lze sledovat a dostatečně včas lze před nimi varovat. Největším nebezpečím tak jsou právě tělesa mezi 1 mm až 10 cm. Jsou těžko pozorovatelná současnými technikami a mohou způsobit v případě srážky masivní poškození komponent vesmírného výtahu.
Konstrukce vesmírného výtahu je velmi masivní a představuje tak velkou plochu vystavenou riziku srážky se zmíněnými objekty. Před jeho stavbou tak bude potřeba vyřešit problém s čištěním nízkých oběžných drah od vesmírného odpadu.
V případě aktivních družic bude potřeba počítat s jejich koexistencí s vesmírným výtahem. Družice i vesmírný výtah tak musí mít možnost se aktivně kolizím vyhýbat. Družice na nižších oběžných drahách totiž kříží rovník několikrát za den. Lze předpokládat, že v budoucnu zvláště třeba s rozvojem GPS a vesmírných komunikací navíc jejich počet poroste a bude dosahovat tisíců. Vesmírná stanice ISS má například oběžnou dobu zhruba 90 minut a rovník kříží každých 45 minut, to znamená zhruba 32krát za den a 11 680krát za rok. Je tak jasné, že plánování různých vesmírných aktivit je třeba koordinovat. Znamená to, že dráhy družic a výtahu je třeba znát s vysokou přesností a na dlouho dopředu, aby bylo možné velikost nutného aktivního vyhýbání snížit na rozumnou míru. Celá konstrukce tak nesmí být úplně pevná a tuhá, ale musí umožňovat pohyb části konstrukce, případně jeho kmity, které umožní nejen zmíněné vyrovnávání posunu těžiště, ale také předcházení kolizím s družicemi a jinými tělesy.
Problémy spojené s riziky kolizí by měly být řešitelné. Je však třeba přesto počítat i s katastrofální destrukcí systému. Hlavně kabiny přepravující lidi by měly mít dostatečné rezervy v zásobování energií i vzduchu v případě uvolnění. Jejich autonomní záchranná pohonná jednotka by měla umožnit zakotvení na oběžné dráze okolo Země. To znamená zabránit zvýšením orbitální rychlosti nekontrolovanému pádu kabin, které budou ve vzdálenosti do 25 000 km od zemského povrchu, do zemské atmosféry. Tyto kabiny mohou být konstruovány tak, že dokáží samotné řízeně přistát nebo se usadí na dostatečně stabilní dráhu, aby vydržely do příletu záchranné mise. Vzdálenost kabiny od povrchu mezi 25 000 km a 47 000 km znamená, že zůstane na zemské orbitě. Kabiny ve vzdálenosti od povrchu větší než 47 000 km musí být naopak schopny snížit rychlost, aby se usadily na dráze vhodné pro záchrannou misi a neopustily zemské gravitační pole.

Závěr
„Ale všechno se zdálo probíhat tak dobře, jak jen si bylo možno přát; a v příštích hodinách skutečně neměl nic lepšího na práci než kochat se stále se šířícím rozhledem. Dosáhl už výše třiceti kilometrů a neslyšně a rychle stoupal tropickou nocí dál. Měsíc nebyl nad obzorem, ale zemský povrch pod ním se prozrazoval mihotavými souhvězdími svých měst a vesniček.“
A. C. Clark: Rajské fontány
Vesmírný výtah by byl jedním z největších konstrukčních děl, které jsou pro současnou civilizaci v principu v dosahu. Pokud by se realizoval, mohl by dramaticky snížit náklady přepravy materiálů na různé oběžné dráhy okolo Země i ven z jejího gravitačního pole. Tato doprava by byla na úrovni podobné železniční dopravě na zemském povrchu. Potřebný pokrok technologií pro jeho realizaci je sice značný, ale je dostupný v relativně blízké budoucnosti.
Obrovskou výhodou je, že většina potřebných technologií má uplatnění i v jiných oblastech a jejich vývoj neprobíhá jen kvůli vesmírnému výtahu. Superpevné materiály, jako je grafen, mohou znamenat zlom v konstrukcích i pozemských staveb. Maglev, elektromagnetické dělo a další elektromagnetické dopravní systémy by mohly znamenat zlom i v pozemské dopravě. Extrémně vysoké budovy a konstrukce jsou stále častější významnou součástí některých metropolí a řada architektů představila i velmi odvážné plány na celá města v jedné výškové budově. Velmi důležitý je i rozvoj schopností budovat velké vesmírné konstrukce na oběžné dráze.
Kosmický výtah není sice systémem, který umožňuje dopravu k nejbližším hvězdám. Je však jasné, že se budoucí hvězdolety budou stavět ve vesmírném prostoru a nelze o nich uvažovat bez vyřešení problému s dopravou materiálu ze Země a dalších těles Sluneční soustavy do vesmíru. I z tohoto důvodu je článek součástí cyklu, který se zabývá možností mezihvězdného cestování. Další články jsou zaměřeny na využití jaderných zdrojů, slunečních plachetnic, gravitačního praku, mikrovlnného pohonu, slunečních baterií, klasickým raketových motorů a ochraně před radiací.
Psáno pro servery Osel a Kosmonautix.
Doporučená literatura
D.V. Smitherman Jr.: Space Elevators, An Advanced Earth-Space Infrastructure for the New Millennium, NASA/CP-2000-210429, 2000
M. L. Cosmo, E. C. Lorenzini: Tethers In Space Handbook, third edition, prosinec 1997, také předchozí vydání z roku 1989
DODATEK
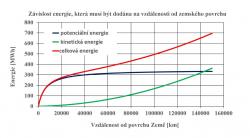
Všem účastníkům děkuji za zajímavou a dlouhou diskuzi. Zvláště pak Pavlu Brožovi, který v obsáhlých, trpělivých a velice srozumitelně napsaných vysvětleních objasnil řadu problémů a nejasností u čtenářů. Pomohl mi tak korigovat i některé nepřesnosti a neobratnosti v textu článku, kterých jsem se dopustil. Hlavně jej však doplnil pro vážnější zájemce v řadě oblastí o přesnější fyzikální a matematický rozbor. A také hodnoty, které ukazují poměr sil, napětí a energií. Je tak možné si udělat lepší představu, co a jak bude pohyb výtahu a jeho parametry ovlivňovat. Na závěr bych si ještě dovolil doplnit graf ukazující, jakou energii je třeba dodat kabině o hmotnosti 20 tun, aby se dostala do různých částí výtahu. Tuto energii by měla kabina získávat ze svého elektrického pohonu a částečně také z rotace Země (ovšem tato energie je vůči celkové hodnotě energie rotace Země zanedbatelná).
A na úplný závěr bych chtěl zdůraznit. Vesmírný výtah je zatím v oblasti vědecké fantastiky. Ani já a ani Pavel Brož nevíme, jestli jej nakonec někdy v spíše daleké budoucnosti bude možné realizovat, nebo se ukáží nepřekonatelné technologické překážky v jeho konstrukci. Na druhé straně je to velmi zajímavý koncept a vize, která se dotýká řady technologických výzev zajímavých pro řadu oborů. Například i v našem ústavu (Ústav jaderné fyziky AV ČR) se zabýváme studiem vlastnosti grafenu pomocí jaderných analytických metod a snažíme se pomoci při hledání cest pro jeho výrobu v masivním měřítku pro využití jeho zajímavých vlastností.
Výsledky vesmírných výtahových her pro rok 2009
Autor: Jan Bílek (13.11.2009)
Vesmírný výtah – proč tu již není?
Autor: Jan Bílek (25.01.2010)
Vesmírný výtah – proveditelnost z pohledu pevnosti lana a výkonu zdviže
Autor: Jan Bílek (28.02.2010)
Vesmírný výtah – pokus o odpovědi na otázky
Autor: Jan Bílek (21.04.2010)
Gravitačním prakem střílíme do mezihvězdného prostoru
Autor: Vladimír Wagner (19.08.2016)
Raketové nosiče – pořád trochu sázka do loterie (+ aktualita Tiangong 2 )
Autor: Vladimír Wagner (15.09.2016)
Jak vypadá situace okolo mikrovlnného (EM) pohonu
Autor: Vladimír Wagner (29.11.2016)
Stratosférický balón - let Fík 2
Autor: Vladimír Wagner (15.03.2017)
Diskuze:
Lano Vesmírného Výtahu bude sadomasochisticky bičováno mikrometeory energie větší než 140 J cca 10x denně
Josef Hrncirik,2017-09-12 21:44:15
podle fig. 26 p.26 z odkazu NSA/CP-2000-210429
,který mylně předpokládal lano tloušťky 1 mm, s pevností (nosností) 10 t.
Při pevnosti (napětí v tahu) 100 GPa by tržná délka lana byla cca 6000 km. Pokud by se počet lan po polovině tržné délky zdvojnásobil, aby to dole uneslo 10 t, hmota lana k GSO by ale musela být cca 6 ti násobná a průměrný průřez tedy cca 3 násobný a lano by se tedy bičovalo cca 30x denně (ev. při nesení 15 t cca 42x).
Energie 140 J dokáže roztavit 3 mm3 graf(itu(enu)(délku 1,4 mm lana průměru 1,4 mm nesoucího 15 t.
140 J nese meteor průměru 0,7 mm pomalý 20 km/s.
Na přeražení grafenu určitě stačí mnohem menší energie a smrtelné bičování tedy bude mnohem častější než po půlhoďce odpočinku.
Bude bičované lano Vesmírného Výtahu Atilla (Flagellus Dei) vypráskávající orbity?, nebo jen jednorázový Fulmen Dei?, či až 5000 s svítící Edisonova uhlíková žárovka?
Josef Hrncirik,2017-09-13 09:29:10
Z knihy sovětských vědců vylepšujících ablativní návratové štíty MIRV k dokonalosti
(na Scihub pod DOI) 10.1007/978-3-319-21349-1
"Uhlík při vysokých teplotách" je zcela zřejmé, že diamanty ani graf-en;it ničím nenahradíš, rozhodně ani karbidy či výpomocí s kovovou matricí.
V Institu elektroexplozí, který vyvinul k dokonalosti iniciaci sférické imploze jaderných bomb; explozivně zahřáli, roztavili a vypařili mnoho grafitu a odpovědně konstatují, že grafit je látka s nejvyšším bodem tání (trojným bodem) a kritickou teplotou a žádné zázračnější materiály být nemohou.
Není šance připravit carbyn či cumulenová či kovová vlákna z uhlíku.
Grafen natažený k mezi pevnosti 140 GPa má při modulu pružnosti E = 1 TPa protažení e = 14%, tj. 0,14 relativně.
Absorbuje tedy deformační (elastickou, využitelnou) práci 1/2*E*e**2=5*10**11*0,14**2=9,8 GJ/m3=9,8 GJ/2200 kg = 4,5 MJ/kg = nesporně výbuchová energie 1 kg TNT.
Tato energie sice zahřeje po svém uvolnění svého nositele (grafit) na 2 700K, ale protože grafit je nejméně těkavá látka, tlak par uhlíku je max. jen cca 20 Pa a je mnohem menší něž atmosférický a ke klasické explozi tlakem plynu nemůže dojít.
Při minulém výpočtu jsem tam numericky opomněl vynásobit druhou mocninou deformace, (jen první) a proto mi vyšly jasné exploze energií 32 MJ/kg, kdy je uhlík roztaven vysoko nad trojným bodem 4900K při tlaku páry 10 MPa a ohřát na taveninu až 10000K s tlakem par 200 MPa, kdy pak noha parou (karbonu) cválá lépe než s pouhým CL-20.
K této superexplozi tedy dojde jen v grafenových setrvačnících rozfofrovaných na pevnost grafenu 140 GPa ;
Tam podle vztahu hustota uložené energie = pevnost/hustota = 140GPa*m3/2200 kg = 38 MJ/kg = určitě 7kg TNT, i kdyby 2,5 kg TNT zůstaly ve žhavém uhlí 5000K o tlaku par pouhých 10 MPa. Tak to bude vidět i Báňský úřad.
Pokud bude našponovaný konec lana při diverzní akci uvolněn láskyplně, něžně, a plynule s nezbytným bržděním, šlehající lano by se mohlo stát Chladným Bičem Božím, alespoň pro první část kmitu či první kmity.
Pokud se však porušení lana bude více podobat iniciaci nárazem (rozbuškou) lano si vzpomene na pád řady dominových kostek (či spíše na řetězovou reakci následných implozí řady dotýkajících se baněk evakuovaných k mezi pevnosti po iniciaci jedné z nich).
Lano půjde do kompromisu.
Cca 1/3 energie tj. řekněme 1,5 MJ/kg přejde do kinetické energie trosek lana tj. rychlosti 1700 m/s, tj. měrného impulzu 1700 N.s cca střelného prachu;
2./3 energieohřeje trosky na cca 1000°C a zbytek energie zůstane v poruchách struktury mřížky trosek.
Explozí tedy bude lano svítit příjemně oranžovým teplým světlem táboráku.
Domnívám se, že grafen není natolik houževnatý aby ustál bez křehkého lomu první fázi nárazu od urvaného konečku rychlostí cca 2,9 km/s (z poč. 4,5 MJ/kg) vyvolané z uvolněného tahu přesně do kolizního směru s neuvolněným grafenem.
Detonační tlak 43 GPa se šíří reakcí ve výbušnině CL-20 rychlostí cca 10 km/s bez problémů, přestože musí dojít k fyzikálnímu přeskupení atomů a vytvoření nových vazeb. U grafenu jde jen o uvolnění pnutí do vibračního kmitu a tlakový skok nejméně 140 GPa z uvolněného pnutí pevnosti.
Nelze tedy předpokládat, že po laně poběží pokojná tepelná vlna 2700°C a lano bude svítit jako zakázaná kryptonová žárovka bez destrukce lana a po vychládnutí bude pouze vydezinfikované.
vliv Měsíce
Jakub Beneš,2017-08-27 14:42:25
chybí mi tam zmínka o gravitaci Měsíce, který bude přece celou soustavu každý den vychylovat do různých stran, ne?
Mně osobně by se nejvíc líbil výtah, který be nebyl pevně ukotven na povrchu, ale pouze zavěšen v nějaké výšce, kam ještě doletí letadla. tam by se přesedalo. (předpokládám výtah pouze pro lidi, neživé náklady by se vystřelovaly elektomagnetickým dělem a nezatěžovaly zbytečně výtah) nepochopil jsem nikdy, proč je nutné to spojení s povrchem, kromě toho, že to ulehčí nakládku.
Re: vliv Měsíce
Pavel Brož,2017-08-27 15:14:17
Ten náklad se vynáší do výšky 35800 km, zatímco letadla dostoupají do dejme tomu 20 km výšky, těch ušetřených 20 km je tedy z hlediska celkové energie potřebné na vynesení nákladu zanedbatelná úspora, které nestojí za ty šílené komplikace při překládání nákladu vyhozeného z letadla na tu kabinu výtahu.
Ano, Měsíc samozřejmě bude působit ochylky od přesně kruhové dráhy, působí tak samozřejmě i na stávající geostacionární družice. Odchylka od přesné kruhové dráhy působená gravitací Měsíce bude v řádu několika málo stovek metrů (z hlavy mi to vychází kolem dvou set metrů), a řádově stejně velká bude i pro vychylování stanice a protizávaží do stran. Vzhledem k těm vzdálenostem půjde o extrémně malé úhlové odchylky v řádu desetitisícin stupně při pohledu ze zemského povrchu.
Mimochodem ale to lano ukotvené dole opravdu bude užitečné v některých případech uvolnit a nechat vytáhnout o cca dvacet kilometrů nahoru. Např. v situaci, kdy se do oblasti ukotvení bude blížit hurikán, ona sice ta oblast kolem rovníku je mnohem klidnější než jiné oblasti, to ale neznamená, že by v ní minimálně prudká bouře nemohla čas od času vzniknout. Vytáhnutí lana nahoru a jeho opětovné spuštění po bouři je mnohem jednodušší a rychlejší operace, než složité manévrování s ukotvenou plovoucí základnou, nehledě na problém vzniklý např. tehdy, kdy by se bouře nedejbože stočila právě směrem, kterým se jí ta plovoucí základna pokouší vyhnout. To vytažení lana o dvacet kilometrů a jeho pozdější spuštění se opět dá kompenzovat příslušným přitažením a pozdějším uvolněním toho druhého lana k protizávaží.
Re: Re: vliv Měsíce
Milan Krnic,2017-08-27 16:39:17
Jenže ono to i dle vizualizace NASA nebude lano, jen se to jako lano zjednodušuje.
No a navíjejte na něco trubku :)
Re: Re: Re: vliv Měsíce
Pavel Brož,2017-08-27 17:43:48
Ona to opravdu nebude trubka, bude to lano. I velmi tlusté lano můžete navíjet, pokud je správně spleteno z jednotlivých pramenů, navíjejí se i velice tlustá ocelová lana. O trubku opravdu nepůjde.
Navíc ta vizualizace koresponduje s opravdu obřím výtahem, kdežto ze začátku se bude realizovat něco mnohem skromnějšího. Asi takový úplně nejskromnější výtah by měl mít hmotnost spodního lana kolem 750 tun a provozní hmotnost kabiny s nákladem kolem 20 tun. Při požadované pevnosti 100 GPa vychází ta tloušťka lana při kruhovém průřezu řádově v milimetrech.
Wigner effect
Josef Hrncirik,2017-08-26 11:24:21
Při akumulaci 2,7 MJ/kg pnutím v grafitu se může po malém impulzu uvolněnou energií zahřát až na 6780°F.
Pro grafen wiky píše:
pevnost 130 GPa; modul pružnosti v tahu 1 TPa; hustota tajná (asi cca grafit, tj. 2,3);
odtud: protažení při přetržení 13%; akumulovaná elastická energie 65 TJ/m3 = 28 MJ/kg,
tj. 10x více než max. Wigner effect.
Ekvivalentní max. W.e. je pnutí (v laně) 40 GPa.
4 MJ/kg TNT by odpovídalo pnutí 49 GPa.
Vzhůru na orbity.
Re: Wigner effect
Vojta Ondříček,2017-08-26 11:59:05
Elasticita, budiž pružnost, je pro výtahové lano do Vesmíru krajně nevhodnou vlatností. V případu Vesmírného výtahu by narůstající mechanické napětí toto lano prodlužovalo, což by vedlo nárůstu napětí a k podélným oscilacím. A to i v případu aktivního posouvání protizávaží. Bez regulačního zásahu by nastala katastrofa.
Jeden z Murphyho zákona zní "co se může pokazit, tak se někdy pokazí".
Takže, jak píšete, efekt napnutých šlí a utrženého knoflíku na šli.
Re: Wigner effect
Josef Hrncirik,2017-08-26 21:45:51
Při napnutí v (zásadě jakéhokoliv očekávaného lana) na pnutí 100 GPa uváděné jako již technicky přijatelná pevnost pro výtah,
pak 1 kg takto našponovaného lana má naakumulovanou energii odpovídající 4 kg TNT (energie roste s kvadrátem pevnosti).
1 kg lana pak je schopen v zásadě explozivní rychlostí uvolnit energii odpovídající 2 kg nejsilnější klasické výbušniny CL-20 či 3 kg RDX.
Detonační vlna se šíří rychleji než rychlost zvuku ve zplodinách.
Určitě tedy bude rychlejší než rychlost zvuku v napjatém grafenu 20 km/s a rychlost zvuku v diamantu ?cca při 6000°C (v tabulkách se neuvádí).
Proto se chemici DARPA snaží připravit metastabilní (napnuté) modifikace uhlíku jako supervýbušninu (?kraken).
Pochopitelně jako u každé výbušniny pro dosažení maxima detonační rychlosti výbušnina musí mít dostatečný průměr a hustotu.
Jinak se detonace nerozvine max. rychlostí či dojde k podzvukovému šíření (8 km/s jako max. hexogenu) či deflargaci (hoření) ? řekněme 1-5 km/s.
K roznětu trhacích prací se běžně používá a postačuje 2 g rozbuška č.8, hexogenová je nejlepší.
Nejspíš bude stačit i trocha termitu či plamen či stlačení prudkým nárazem mezi 2 kovovými povrchy.
Grafen, zejména napnutý je křehký.
Některé kovy (slitiny) mají plastickou deformaci při přetržení i 100% a odpor proti růstu trhlin i řádově větší než grafen, pevnost a modul ale mají řádově nižší a hustotu asi 3x větší.
Na kvalitní lano-výbušninu jako u napnutého grafenu tedy nemají a DARPA nezajímají.
Změna záporného tlaku (tah) na tlak po scuknutí či i na jen atmosferický v zásadě odpovídá tlakovému skoku v detonační vlně TNT, navíc má příhodnější směr přímo do kolize s novým materiálem bez výrazného rozletu do okolí a ztráty impulzu do patřičného směru.
Bojím se, že straším.
Re: Re: Wigner effect
Vojta Ondříček,2017-08-26 22:19:34
S akumulovanou energií v napnutém lanu nejsou žádné žerty.
Dost možná, že prasklý vypínací drát skeletu vzducholodi Hindenburg proťal při přistávycích manévrech v Lakehurstu poslední vodíkový balon a unikající vodík elektrostatickým výbojem vzplanul.
Re: Re: Re: Wigner effect
Milan Krnic,2017-08-27 09:56:38
Kromě toho třeba ta hypotetická konstrukce výtahu nebude pouze lano, viz obrázek první.
Zjednodušení je na prd. Jak níže uváděl pan Wagner, cituji "Ve vesmíru se začíná testovat".
Tedy uvidíme.
(to bude zas smetí)
To nebude tak zlé
Vojta Ondříček,2017-08-27 13:43:18
Testuje se na nízkých orbitech a tam to "smetí" nevydrží dlouho.
Na konci lanka musí být tak jako tak nějaká jednotka s reaktivním pohonem na jeho "vytažení" ze zásobníku a na aspoň prvotní stabilizaci. Čet jsem kdysi o takovém pokusu (nevím už jestli to bylo na ISS), to lanko se začalo chaoticky chovat a muselo být "odhozeno".
Re: To nebude tak zlé
Milan Krnic,2017-08-27 16:32:15
A pokud se i v rámci tohoto něco "nepodaří", bude v záloze Sandra Bullock a 4K 3D kamera (když už zde probíráme hypotézy). :)
kratší nesynchronní výtah na zemi
Petr Ženč,2017-08-26 01:20:29
Děkuji za velice zajimavý a podnětný článek, stejně jako podnětnou diskuzi.
V textu jste se zmíňil o kratších nesynchronních výtazích na marsu z měsíců ..že by tyto výtahy byly proveditelné již se současnými materiály lan.
Uvažuje se, že by podobný systém byl předchůdcem vesmírného výtahu na zemi?
Příjde mi, že takový demonstrátor na geostacionární dráze země - pokud by byl ekonomicky smysluplný - bude jedním z dalších kroků.
Re: kratší nesynchronní výtah na zemi
Vladimír Wagner,2017-08-26 23:00:32
Vesmírný výtah, o kterém se dominantně uvažuje, je kotvený a synchronní. A přesně ten se intenzivně rozebírá v článku a diskuzi. Ve vesmíru se začíná testovat a plánuje se řada jednodušších konstrukcí. Třeba družice visící na dlouhém laně připojeném ke stanici na vyšší orbitě, které dlouhodobě zkoumají podmínky na relativně nízkých oběžných drahách s velkým odporem vzduchu. Nebo konstrukce využívající moment hybnosti a rotaci rozsáhlé konstrukce pro nahrazení gravitace. A také pro dopravu nákladu mezi orbitami. Ekonomika takových systémů závisí na podmínkách, které jsou potřeba pro jejich provoz, a dostupných technologiích. V každém případě se při jejich postupném rozšiřování otestují technologie potřebné pro vesmírný výtah.
Web s dalsim info
Petr K,2017-08-25 08:44:43
Neni spatny nasledujici web:
http://www.zadar.net/space-elevator/
Spousta zajimavych informaci, cisel, grafu :) Napr. ze na Marsu na stavbu vesmirneho vytahu kevlar bohate staci.
ad strašení Coriolisovou silou
Pavel Brož,2017-08-24 15:22:09
Protože to tady zaznělo, je vhodné uvést na pravou míru i onen mýtus o tom, jak Coriolisova síla působící na vynášený výtah všechno zhatí. Takže mějme lano ukotvené u zemského povrchu nataženého ze stanice na geostacionární dráze ve výšce 35800 km nad tímto povrchem. Nad geostacionární stanicí je nataženo protizávaží, které vytváří (při kabině už zavěšené na laně) nadbytek tahu ekvivalentní pozemské tíze 3 tuny, tj. cca 30 kN. Předpokládejme hmotnost kabiny 20 tun, a její rychlost směrem nahoru 1000 km/h. Při této rychlosti bude Coriolisova síla působící na kabinu rovna F_c=2*m*omega*v, kde m je hmotnost kabiny (20000 kg), omega je úhlová rychlost Země (omega=2*pi/86400=7,272*10^-5 s^-1) a v je ona rychlost kabiny (v=1000 km/h=278 m/s). Dostaneme tedy Coriolisovu sílu rovnou F_c=808 N. Toto je tedy ona boční síla působící na kabinu a tím i lano v plné rychlosti 1000 km/h.
Tato boční síla působící na lano se složí s přebytkem tahu 30 kN, takže máme výslednou sílu s radiální složkou 30000 N a tangenciální složkou 808 N. Výsledná síla bude odkloněna od kolmice o úhel 1,54° směrem na západ.
I kdyby tato síla působila na lano po neomezeně dlouhou dobu (ona ve skutečnosti bude působit pouze po dobu 35,8 hodin potřebných k vynesení té kabiny nahoru, protože na geostacionární dráze se kabina zastaví a spolu s tím zmizí i tangenciální Coriolisova síla na ni působící), tak jediným "hrůzostrašným" výsledkem by bylo, že geostacionární stanice by zůstala vychýlena o těch 1,54° směrem na západ od kolmice vedené z bodu ukotvení lana, to je všechno. Názornou představu si lze udělat na základě obrázku zde:
https://en.m.wikipedia.org/wiki/File:Space_elevator_balance_of_forces--circular_Earth--more_accurate_force_vectors.svg
(nenechte se pouze zmást tím, že úsečka nad kabinou míří viditelně jiným směrem, než původní kolmice, je to dáno pouze zveličením zakřivení Země na tom obrázku - úsečka nad kabinou samozřejmě bude mít směr radiály vedené ze středu Země nahoru)
Takže i kdyby ta Coriolisova síla působila neomezeně dlouhou dobu, tak jediný důsledek bude, že geostacionární stanice bude trvale vychýlena o 1,54° směrem na západ, toť vše. Ve skutečnosti ta síla se zastavením kabiny v cíli cesty zanikne, tím pádem se vychýlená geostacionární stanice i s protiváhou začne (díky tomu přebytku tahu) vracet do původní polohy, tedy přesně kolmo nad bod ukotvení lana dole na Zemi. Uvažujeme-li hmotnost lana 750 tun, stejnou hmotnost protizávaží, hmotnost stanice 1000 tun, tak se dá spočíst, že doba kmitu bude cca 106 hodin (ve výpočtu je přitom nutné zohlednit rozložení těch celkových 2500 tun mezi lano, stanici a protizávaží s využitím známého integrálního výrazu pro výpočet momentu setrvačnosti).
Můžeme se ještě podívat, jak hrůzostrašné přepětí toho lana ta Coriolisova síla způsobí. Takže bez ní musí lano kromě své vlastní váhy umět udržet i tu kabinu o hmotnosti 20 tun a ten přebytek tahu ekvivalentní 3 tunám. Kromě napětí potřebného k udržení vlastní tíhy bude tedy lano s kabinou vystaveno dodatečnému tahu 23 tun, tedy 230 kN. K této radiální složce přidáme tedy tangenciální složku působenou Coriolisovou silou o velikosti 0,808 kN, snadno tedy spočteme, že nově bude lano vystaveno tahu 230,0014 kN, tedy o 1,4 N vyšším než při zastavené kabině, kdy Coriolisova síla nevzniká.
Jinými slovy, ani s přepínámím lana v důsledku Coriolisovy síly žádný problém nevzniká, veškeré nekompetentní připomínky typu lano není žádný nosník atd. jsou tedy úplně mimo.
Co se týče energie potřebné k urychlení na nové oběžné dráze, tak toto není nic co by bylo třeba řešit nad rámec energie potřebné pro stoupání kabiny. Autonomní pohon v kabině zajistí stoupání nahoru, urychlení v tangenciální směru jde na úkor nepatrného zmenšení rotační energie Země, tuto energii není potřeba dodávat (rotační energii Země se tato zapůjčená energie zase vrátí po opětovném snesení stejně těžkého nákladu dolů).
Takže to je asi tak vše, co je možné říct k otázce údajných katastrofálních účinků Coriolisovy síly působící během vynášení kabiny na lano.
Premazane?
Radoslav Porizek,2017-08-24 00:19:03
Pozeram, ze moj predchadazajuci prispevok nejak zahadne zmizol.
.
Takze pochvala atomovemu fyzikovi, ze sa takto pekne zasnival o vesmirnom vytahu.
Mne osobne pride fascinujuce, ze vieme, ze existuje struktura (nanorurky), z ktorej by sa dalo spravit dostatocne pevne lano pre kozmnicky vytah, ale bohuzial ju zatial nedokazeme vyrobt. A to sa snazime uz par desatroci, takze je celkom realne, ze ju nevyrobime v dostatocnom mnozstve a kvalite nikdy.
.
Co sa tyka inych technickych pripomienok k vesmirnemu vytau, tak cca. pred 20 rokmi, ked sa verilo, ze sa nam lano s nanotrubok podari v dohladnej dobe vyrobit, tak sa tieto problemy vedecky riesili a verilo sa, ze sa daju tecnicky zvladnut. Dokonca si spominam na naprojektovanu cenu cca. 500 USD za vynesenie cloveka na obeznu drahu vesmirnym vytahom ( sucasnoti je cena za 1kg zhruba porovnatelna z cenou zlata)
Re: Premazane?
Juraj Chovan,2017-08-24 12:06:38
Nazdar Rado,
rad Ta stretavam na oslovskej diskusii :)
Mas pravdu, pamatam sa ako sme pred tymi 20 rokmi debatovali ze mame prve nanotrubky, do par rokov to budeme vediet komercne vyrabat a potom bude aj ten vytah...
Mam z toho podobny dojem ako z jadrovej fuzie, kde je 30 rokov do realizacie konstantou uz pomaly 3/4 storocia...
Kazdopadne je to tema ktora ma nadchynala vtedy a nadchyna ma aj teraz - zeby dalsia konstanta? :)
Trocha matiky
Jiri Matus,2017-08-22 19:46:37
Tak jsem si spočítal tu boční sílu.
z nuly na 3,1 km/s horizontální rychlosti za 35 hodin (=35*60*60 sekund).
v = a * t
3100 = a * 35*60*60
a = 0.025 m/s^2
při hmotnosti nákladu řekněme 10t = 10000 kg
F = m * a
F = 10000 * 0.025
F = 250 N
tedy boční síla 25 kg
Možná mám někde špatné jednotky, prosím o kontrolu.
A ještě jedna věc, někde dole se řešilo teplo... myslím, že ta dodaná energie (14kWh) se přemění ne na teplo, ale hlavně na potenciální energii, ne?
Ale hlavně díky za skvělý článek a podnětnou (i když vyčerpávající) diskuzi.
Re: Trocha matiky
Vojta Ondříček,2017-08-22 20:26:27
V podstatě OK, až na to, že těleso na rovníku má už kruhovou rychlost 0,47km/s, takže na ty 3,1km/s na GEO zrychluje jen o 2,6km/s.
Nosné lano, v konstrukčním příkladu, který jsem uved nížejc, disponuje podél své délky stoupajícím "napnelismem" vrcholícím na GEO v hodnotě 570kN (odpovídajíc zhruba tíže hmoty 57 tun na rovníku.) Platí pochopitelně jen pro klidový stav.
Coriolisova síla vámi vypočtená na 250N je v poměru k "napnelizmu" lana od ukotvení 10kN po maximum 57kN celkem malá, (2,5% až 0,44%).
Omluva
Vojta Ondříček,2017-08-22 23:48:41
za překlepy:
Coriolisova síla vámi vypočtená na 250N je v poměru k "napnelizmu" lana od ukotvení 100kN po maximum 570kN celkem malá, (0,25% až 0,044%). Přesto "vytlačí" tu stanici na GEO tak desítku km západním směrem. Na velikost síly v nosmém lanu to nebude mít prakticky žádný vliv (zlomek procenta).
Děkuji za pochopení, stresovaný V.O.
Trochu oleje na rozbouřenou hladinu.
Vojta Ondříček,2017-08-22 19:36:07
Pro pana Nováka.
To nosné lano výtahu do Vesmíru musí být
1. ukotveno někde na rovníku (nebo poblíž) a
2. musí mít vysoko nad GEO (Geostationary Earth Orbit) protizávaží, které zaručí nějakou minimální sílu v bodu ukotvení. Navrh bych kotvící sílu 100kN pro systém transportující masu 10t ("kabiny").
Když se začne pohybovat "kabina" od povrchu ke GEO, tak, jak správně poznámenáváte, změnou výšky "kabiny" se vybudí Coriolisova síla. Ta způsobí jak prohnutí napjatého nosného lana, tak změnu výšky a pozice protizávaží nad povrchem Země a tím pokles napínací síly nosného lana. Je jasné, že nesmí dojít ke stavu, kdy síla lana v bodu ukotvení na povrchu se přiblíží nule. Dejme, že jí povolíme hodnotu 50kN, tím že regulujeme rychlost "kabiny" (platí samozřejmě jak pro směr nahoru, tak dolu).
Lano i protizávaží se tedy vychýlí z původní stabilní polohy a jakmile se "kabina" zastaví, bude se vše vracet do původní polohy a překmitne. A zde nastává zřejmě problém s kmitající soustavou, neboť nejsou kmity samy od sebe tlumené. Proto existují přestavy o pohyblivých protizávaží, které by měly aktivně změnou své vertikální polohy ony kmity kompenzovat. Další netematizovaný problém může být v elesticitě lana a tedy i v podélných kmitech.
A snad ještě poznámky (pro všechny a asi zbytečné).
1.
Jakékoliv těleso na oběžné dráze má energii potencionální, danou výškou na gravitačním těžištěm a kinetickou danou rychlostí (jeho momentální trajektorie).
Těleso vypuštěné na jakémkoliv výškovém bodu našeho výtahu se bude pohybovat po eliptické křivce. Bude-li místo vypuštění zhruba pod dvacítkou tisíc km nad povrchem, protne tato dráha zemský povrch. (odkoukal jsem z jednoho grafu). Chtěli bysme umístit těleso na kruhovém orbitu, řekněme 500km nad povrchem (Hubbleteleskop), musíme mu po vypuštění z výtahu změnit dráhu reaktivním pohonem.
2.
Na GEO se to hemží satelity pro televizní přenos a na takzvaném "hřbitovním" orbitu o kousek výš, vysloužilými satelity. A míň jich nebude. Pro kmitající "základnu" vesmírného výtahu asi nelibá situace.
3.V tabulkovém kalkulátoru mi při kotvícím tahu 100kN, "kabiny" o hmotnosti 10t a užitné pevnosti lana 100GPa a celkové délce 100 tisíc km vyšla masa protiváhy na konci lana skoro 690tun a celková hmotnost lana 1100tun - to vše musí být nějak vyneseno na GEO, nelehký úkol.
To nepomůže.
Jiří Pospíšil,2017-08-21 21:16:59
Fakt si to namalujte a pak natáhněte jedno z těch dvou lan do trojúhelníku do boku jak tětivu, což udělá stoupající náklad bez bočního stálého zrychlování, třeba raketou zcela zákonitě. A čistě fyzikálně, abyste dostal těleso na dráhu, kde by letělo s tou geostacionární stanicí lanovky současně, v ní, vedle ní, u ní, potřebujete furt stejně energie, ať tam letí raketa nebo co. Nebo popojíždí po výtahu. Každá, sebemenší boční síla vychýlí bočně i protizávaží. Bude působit se strašlivým momentem. A do boku nedrží to protizávaží nic. Přijatelné jsou jen malé přísně po laně jdoucí síly, které zvýší nebo sníží napětí lana, které bude napínáno odstředivou silou. Ony i pohyby zemské osy, které vedou k tomu, že místo na rovníku není pořád na rovníku s tím protizávažím docela zacvičí. A navíc ve směru kolmém k silám, kterými bude na lano působit stoupající nebo klesající kabina. Nějaká protikabina nebude mít taky smysl, protože jednak nebude vždy stejně těžká, jednak nebude působit ve stejném místě a už vůbec ne stejným momentem na protizávaží. Lano takové délky nemůže mít žádnou boční tuhost. Fyzika se moc oblafnout nedá. Abyste něco dostal na oběžnou dráhu, tak tomu musíte dodat první kosmickou rychlost. Ne nahoru, ale tečně do boku. To jenom tady furt panuje představa, že rakety létají nahoru. Tak jen startují, aby při startu nedrhly o kosmodrom. Jde o rychlost ve vztahu k zemi doboku. Přitažlivost zařídí, aby satelity létaly dokola.
A o těchto banálních maličkostech se tady nějak furt nemluví, nikdo neprovádí výpočty a po těch letech mám obavy, že většina přispívajících ani neví, s čím to furt otravuji a o čem to sakra píšu. Ale každý si může udělat to, co jsme dělali jako malí kluci. To se vezme klacek, k tomu se přiváže na dlouhý špagát šutr a točí se s tím nad hlavou. A pak se vezme druhý klacek a strčí se nahoru, aby zbrzdil ten špagát a dějí se věci. Ten šutr nesmí být velký, protože ten švunk, s kterým se nakonec přiblíží tomu středu otáčení by mohl i ubížit.
Re: To nepomůže.
Juraj Chovan,2017-08-22 11:13:02
Pán Pospíšil, mám dojem že pán Wagner Vám neodpovedá uspokojivo lebo nie celkom pochopil Vašu otázku. Ak som ju pochopil správne ja, pýtate sa, aká zázračná sila má "z boku" pôsobiť na kabínu, lebo ak žiadna, tak kabína bude tým "druhým klackom" ktorý spôsobí že sa celý výťah omotá okolo zemegule.
Ale uvedomte si, že príklad "s klackami a šutrom" funguje ako popisujete iba vtedy ak ten druhý klacek je naozaj masívny klacek (alebo malý ktorý však pevne držíte v ruke). Ak namiesto veľkého klacku použijete steblo trávy alebo tenkú halúzku, nestane nič kritické: šnúrka sa v mieste kontaktu trošku ohne a dľa zákona akcie a reakcie sa ohne aj halúzka.
Pointa je že hmotnosť kabíny je zanedbateľná voči hmotnosti lana s protizávažím na konci. Áno, máte pravdu že zotrvačný pohyb kabíny spôsobí ohnutie lana (takže úsek lana "pred" kabínou nebude v tej istej priamke ako úsek lana "za" kabínou). A práve toto malé ohnutie vygeneruje tú zázračnú bočnú silu ktorá Vám chýba a ktorá spôsobí že kabína bude aj v bočnom smere zrýchľovať. Keďže je však odstredivá sila lana s protizávažím oveľa väčšia ako zotrvačná sila kabíny, nie je pravda že výťah sa v dôsledku pôsobenia kabíny zamotá.
Čo sa týka Vašich poznámok že lano v bočnom smere nemá žiadnu pevnosť, nie je to nosník atď...: To samé sa vzťahuje na systém klasických lanoviek ktoré vidíme v lyžiarskych strediskách. Sedačka s lyžiarmi taktiež pôsobí na lano lanovky v priečnom smere, nie v pozdĺžnom. A napriek tomu sa zatiaľ žiadna lanovka kvôli tomuto priečnemu pôsobeniu nezrútila a jej lano sa neprethlo. Áno, v mieste kde je sedačka na lane zavesená tak tam je lano mierne ohnuté, ale to neznamená že to spôsobí nejakú divergentnú nerovnováhu kvôli ktorej systém skolabuje. A podobne je to aj s vesmírnym výťahom: Je pravda že kabíny pôsobia na lano, ale zároveň aj lano pôsobí na kabíny, takže vo výsledku je ten systém síce dynamický ale zároveň aj stabilný.
Re: To nepomůže.
Vladimír Wagner,2017-08-22 11:53:36
Pane Pospíšile, většinu už Vám odpověděl pan Chovanec, takže já jen doplním. Pokud chcete dostat těleso na geostacionární dráhu, tak mu nemusíte dodat k zemi do boku rychlost první kosmickou (7,9 km/s), stačí pouze několikrát zde uvedených 3,1 km/s. Pochopitelně mu musíte dodat celkovou energii, která je dána potřebnou změnou potenciální a kinetické energie. Teď jen záleží na tom, jestli to uděláte optimálním způsobem ještě s přispěním příspěvku energie odebrané z energie rotačního pohybu Země (z hlediska její velikosti zanedbatelný, ale z hlediska Vašeho malého nákladu už ne), nebo ne. A právě vesmírný výtah by tento optimální způsob mohl umožnit.
Marek Sysel,2017-08-21 19:14:54
Dobrý den, tuším, že pan Hrncirik zde zmiňoval nunchaku a bolasa, čímž mi vnukl myšlenku... Mluví se vždy o výtahu ukotvenem v jednom místě. Nic ale přece nebrání (kromě materiálu) ukotvit ho na dvou místech, na rovníku, a využít tak stabilizacnich vlastnosti trojúhelníku,s výtahem v jeho výšce.
Ale už teď, jak to píšu, predstavuji si spodní konec výtahu, jak pochoduje z V k Z a zpět a to zběsilé nakládání za pochodu... :D
Další článek, který nedbá toho,
Jiří Pospíšil,2017-08-21 17:35:27
že soustava země, lano protizávaží bude reálná sestava v točivé soustavě.
Zvedaným předmětům (kabince) bude při zdvíhání třeba zvyšovat boční rychlost, protože jinak by vyvíjelo značnou sílu kolmou k lanu. Toto zvyšování bude takové, aby z rychlosti 1667km/hod kolmé na lano, dosáhlo ve výšce 144 000 km od středu země tedy na kruhové dráze stále nad základnou lana, rychlosti 18 840 km/hod. Nebude-li na kabince nějaká raketa, nepomůže nic, protože protizávaží není pevným bodem ve vesmíru a jakákoli síla přenesená přes lano do boku na protizávaží vytvoří vektor, který se projeví a způsobí, že kabina, lano i protizávaží se začne oproti kolmici k zemi zpožďovat a nakonec se lano namotá na zemi a protizávaží do země dost velkou energií praští.
Vždyť si to každý zkuste s kuličkou na gramofonové desce.
Někdo by si už konečně mohl přečíst o Coriolisových silách a jak je to s točivými soustavami. Nebo se kouknout na bruslaře a jejich piruety a tak.
Stejně tak rozpružení soustavy do kmitů (k vyhýbaní se tomu smetí) pro vyhýbání povede k velmi zajímavým pohybům protizávaží. To není kolíček na kytaře. To je volně umístěné protizávaží a každý jeho pohyb do boku se vymstí, pokud nebude kompenzován promyšleným silovým působením, třeba raketou na něm umístěnou.
Stejně nedomyšlenou je představa využití smetí na zvyšování hmotnosti protizávaží. To smetí létá na velmi různých drahách a doletět k němu, změnit jeho dráhu, dopravit k protizávaží, tam uvést do stejného pohybu a zafixovat je energeticky vzato šílenstvím.
Vždyť si to už někdo doopravdy spočítejte, když pohyb v otáčivé sestavě je mimo vaši představivost.
Každá tuna dopravovaná ze země, musí být zrychlena z tisice skoro sedmiset km/hod na 18840 km/hod. Zeptejte se třeba mašinfíry, ten vám potvrdí, že to není jen tak, udělit větší hmotě rychlost. A to hodně rychle, protože jinak se doručení do cíle nedočkáte. A kila tam tahat nemá moc smysl. A furt se nějak nemluví o tom, jak tam to lano dostanete a jak skutečně vybudovat protizávaží. I když to budete budovat s geostacionární dráhy, tak i tam se to musí vše dopravit. A i to lano strkané směrem k zemi se bude muset brzdit, jinak se na zem nikdy netrefíte. A směrem k protizávaží zrychlovat, aby to zůstalo na kolmici. Než budete mít protizávaží, tak každou část lana s posunutím zrychlit na jinou rychlost. Jinak nezůstane rovné. jako ta čára po kuličkce na gramofonu.
Jo a ty rychlosti na povrchu země a na geostacionární dráze jsou v článku taky špatně.
Re: Další článek, který nedbá toho,
Vladimír Wagner,2017-08-21 18:41:54
Pane Pospíšile, toto je populární článek, takže by možná bylo dobré se podívat do odbornější literatury o tomto tématu, třeba začít u mých odkazů. Řadu věcí už zde velice pěkně objasnil Pavel Brož. Co mě ale zaujalo, tak je Vaše zmínka, že orbitální rychlosti v grafu jsou u mne špatně. Mohl byste mi prosím napsat správné hodnoty. Na povrchu Země (tedy v grafu nula, protože se zobrazuje vzdálenost od povrchu) je vzdálenost od středu Země 6378 km a nutná obvodová rychlost pro oběžnou dobu necelých 24 hodin zhruba 0,467 km/s, ta je v grafu a odpovídá to i Vámi uváděným necelým 1700 km/h. Geostacionární dráha je zhruba 42 400 km od středu Země a rychlost zde je 3,1 km/s (stejná úhlová rychlost a oběžná perioda jako na povrchu Země). A tato hodnota rychlosti pro tuto dráhu je uváděna i ve všech článcích o geostacionární dráze. Ve vzdálenosti 144 000 km od středu Země by pak měla být orbitální rychlost 10,5 km/s (zase stejná úhlová rychlost a oběžná perioda). A tam mi to už s Vašim číslem nesedí. Já dostávám necelých 38 000 km/h. Tedy o dost větší hodnotu než Vy. Ale možná jsem někde udělal chybu. Takže budu rád, když mi to vysvětlíte. Děkuji.
Re: Re: Další článek, který nedbá toho,
Jiří Pospíšil,2017-08-21 22:07:47
Omlouvám se autore, teprve teď jsem si všiml, že jsem nevynásobil dvěma (blbá chyby ve vzorečku obvodu), takže chybu mám já. Což ovšem znamená, že budete muset při zdvíhání zvyšovat boční sily daleko víc, než jsem varoval. A na to budete potřebovat daleko víc pohonných hmot. Nebo bude boční síla zpomalující a táhnoucí protizávaží dozadu a trochu dolů, s výsledným vektorem smrtícím pro celý systém větší. Tím hůř pro myšlenku výtahu. V nejlepším případě získáte mnohonásobně rozkmitané strunové kyvadlo, když to nedopadne hůř. Jistě, ve věku počítačů se to dá kompenzovat přesně ovládanými raketkami na kabinách, aby vysledně na lano působily jen tahem v ose lana, ale ani to není vůbec jednoduché a už vůbec to nebude provozně levné.
A až teď jsem pochopil, že chcete náklad vytáhnout a pak po vypuštění /odstrčení/ umisťovat na jinou rychlost vyžadující oběžné dráhy. Na což budete muset použít další energii. Brždění nebo zrychlení, vše je ve vesmíru nesmírně drahé.
Ne není to dobře promyšlená věc. I když za tím stojí giganti sci-fi. A scifisti to berou za hotovou věc. Je jedno, kolik lidí na to věří. O takových věcech se nehlasuje.
Re: Re: Re: Další článek, který nedbá toho,
Vladimír Wagner,2017-08-21 23:41:36
Pane Pospíšile, chyby se dopustí každý. I mě se to stává často. Jen mě dost zarazilo, že o vesmírném výtahu diskutujete už od roku 2010 a za celou dobu Vás nenapadlo udělat ani takovou pitomost, jako je si třeba v excellu vynést závislost té orbitální rychlosti na vzdálenosti. A když si jí tedy poprvé spočítáte a vidíte, že je ta Vaše odlišná od té, která je v článku, tak se nekouknete do kopy jiných článků o výtahu a geostacionární dráze. Tam ty rychlosti jsou a zjistil byste, že se od Vás liší všichni ostatní. Máte pravdu, že o takových věcech se nehlasuje, ale, alespoň pro mě by to byla indicie k tomu, abych si své výpočty zkontroloval. Jak pak mám věřit, že jste i o dalších věcech alespoň trochu seriozně přemýšlel a články o nich si alespoň trochu pečlivěji přečetl a uvažoval o nich.
Vesmírný výtah má řadu technologických zádrhelů, pochopitelně jeho budoucí ekonomičnost a efektivnost je velmi otevřená otázka. Ale Vaše poněkud velmi zjednodušená přirovnání o jejich realitě moc neřeknou.
Jen poznámka. I dnes se družice vynášejí na přechodné dráhy třeba i několik jednou raketou a pomocné motory je přepraví na ty konečné pro jejich určení. Když vynesení zajistí výtah a přechod na konečnou dráhu pomocný motor, může být úspora dost velká. Další věcí je, že výtah je hlavně výhodný pro vynášení na vyšší orbity. Ale zdůrazním ještě jednou, jestli se výtah ukáže technologicky dostupný a dostatečně efektivní i ekonomický nelze dnes a ještě dlouho i v budoucnu nebude možno říci. Zatím je to opravdu sci-fi.
Re: Re: Re: Re: Další článek, který nedbá toho,
Jiří Pospíšil,2017-08-22 01:31:05
Ani vy jste se ještě nikdy nevyrovnal s tím, že stoupající kabině bude třeba stálé boční zrychlování, protože jinak prohne lano jak tětivu, a bude táhnout protizávaží z kolmého směru k zemi a dozadu proti otáční země. Odolnost lana v té délce vůči tomuto totiž lze považovat za nulovou. Lano můžete namáhat pouze tahem. Není trámem ani nosníkem. Čím rychleji bude kabina s nákladem stoupat, tím větší bude potřeba bočního zrychlení, aby to nenastalo. Je pravda, že do odkazů jsem nahlédl jen zběžně, ale kupodivu to, že bude třeba rychlost k udržení úhlové rychlosti zvětšit při dopravě zátěže nahoru na vylepšení protizávaží skoro 23 násobně, tam nikdo neřeší. Boční rychlost. Ta sila bude při stoupání pomalém malá, ale bude působit dlouho. Při rychlém stoupání bude velká. Ani fakt, že máte-li do této vzdálenosti kabinu i s nákladem a pohonnými hmotami pro boční rychlost zvyšující raktetky, předpokládejme, že budou instalovány, dopravit nějaký slušný náklad ve smysluplně dlouhém čase, budete k tomu potřebovat slušný výkon raketového motoru, který vydrží pracovat po celou dobu stoupání a bude mít dobře regulovatelný výkon s proměnlivou rychlostí stoupání (nevím, jsou-li takové, co tak dlouho vydrží). A množství paliva k tomuto bude nemalé.
Já se se svou chybou vyrovnal a našel jsem si ji a omluvil se. Ta chyba ale na věci nic nemění. Po její opravě je patrné, že ty boční síly budou ještě větší a jejich vliv závažnější.
Vy jste o řešení bočních sil, reálném problému točivých soustav, zejména lanových, na boční síly citlivých, nenapsal ani slovo.
Dobře, bude se podle článku budovat odprostřed. Ale vy jste se nevyrovnal ani s tím, kterým směrem to lano strkat, aby skončilo na zemi. Ani to není jednoduchý problém. S každým popostrčením směrem k zemi musíte na každém místě už vystrčené délky zajistit, aby vzhledem k zemi byla stejná úhlová rychlost z pohledu od středu země. Tedy, aby každý kousek lana měl rychlost rozdílnou. A strkat někam lano, tak aby zůstalo rovné, je obtížné i na zemi. Pěkných pár tisíc kilometrů vám gravitace v těch místech nepomůže. Ale ty Coriolisovy síly jsou potvory setrvačné, ty v točivé soustavě působí furt, pokud se blížíte nebo vzdalujete od středu otáčení.
Re: Re: Re: Re: Re: Další článek, který nedbá toho,
Vladimír Wagner,2017-08-22 08:48:50
Pane Pospíšile, při dopravě nákladu se s raketovými motory nepočítá. Náklad stačí dopravit geostacionární dráhu, či jen malý kus za ní do místa, kde je orbitální rychlost rovna únikové - hodnota zhruba 4 km/s (proto jsem v článku ten graf s oběma rychlostmi a jejich srovnáním uvedl) a v principu tak máte dostupné všechny dráhy okolo Země i její opuštění (pochopitelně musíte ještě pomocnými motory dosáhnout správný sklon a směr a případně tu rychlost ještě upravit, ale to je třeba řešit u většiny vynášených sond). Pavel Brož velmi pěkně a podrobně vysvětlil představu o fungování výtahu a její energetické hledisko. Moc díky. Jeho příspěvky do diskuzí pod články zvyšují vždy jejich informační hodnotu o více než 100 %. Vždycky mě potěší, když se pod mými články objeví.
Řešení všech problémů spojených s využitím lan a budováním velkých konstrukcí na oběžné dráze bude velmi náročné. A to je vidět i z řady problémů, které nastávají při zatím realizovaných a řadově jednodušších sestavách nyní. Ovšem i v této oblasti se již dosáhlo řady úspěchů a právě zde se dá pracovat na technologických průlomech, které se budou hodit nejen pro ten výtah.
Bilancia
Miroslav Novak,2017-08-21 14:25:53
Aj ked sa na prvy pohlad zda, ze vytah ma energeticky vyhodnejsiu bilanciu v porovnani s raketovym motorom, technicke riesenie, ake je v clanku ponukane, taku bilanciu neponuka.
Pre zjednodusenie vysvetlenia mojho tvrdenia uvediem tieto podmienky, aby sme sa nemuseli zaoberat nepodstatnymi detailami:
- do energetickej bilancie nepocitajme vobec s energiou na vybudovanie a vynesenie zariadenia (nosneho lana a protizavazia) na obeznu drahu Zeme,
- predpokladajme, ze proti nosnemu lanu a protizavaziu neposobi ziadna atmosfera, drobne castice a ulomky na obeznej drahe lana a protizacazia, takze sa pohybuju hypoteticky v dokonalom vakuu. V tomto rezime nie je treba, aby protizavazie malo nejaky pridavny zdroj pohybu, aby bol kompenzovany zdroj strat v nevakuovom priestore,
- ignorujme tiez aj straty, ktore vznikaju nejakym dopravnikom na nosnom lane,
- taktiez ignorujme hmotnost samotneho prepravnika.
Co sa stane, ked budeme chciet po nosnom lane dopravit uzitocne zavazie o hmotnosti m kg do vyšky h na takto zidealizovanom zariadeni?
Budeme musiet spotrebovat energiu, ktora je umerna vztahu m.g.h, kde gravitacne zrychlenie je fciu samotnej h, ak sa nemylim.
Kedze plati zakon akcie a reakcie, o tuto energiu v podobe straty rychlosti pride aj samotna sustava lano/protizavazie.
Aby sme opat uviedli sustavu do pozadovanej rovnovahy (zhodnej uhlovej rychlosti), budeme musiet protizavaziu a nosnemu lanu dodat povodnu rychlost. Ako to urobime? Ze by raketovym motorom na protizavazi? Kde ta raketa ale zoberie palivo?
Myslim, ze moje vysvetlenie je dostacujuce k tvrdeniu z pociatku prispevku, ze energeticka bilancia vesmirneho vytahu je este zufalejsia, ako pouzitie rakety samotnej. Iba ak by sme tej rakete na protizavazi dokazali priviest palivo nie zo Zeme, ale z ineho vesmirneho objektu. Pouzitie slnecnych panelov by prichadzalo do uvahy, ak by sme dosiahli take elektricke vykony, ktore zodpovedaju raketovemu palivu. To je tiez este sen, vsak?
Budem rad, ked ma ktokolvek vyvedie z omylu. O tom je predsa diskusia.
Re: Bilancia
Miroslav Novak,2017-08-21 14:50:16
Ale aby ste ma nepovazovali za pesimistickeho cloveka, nasa spolocnost ponuka, naopak, velmi optimisticke riesenia problemov, ktore su v clanku velmi zaujimavo popisane. Skusim sa spojit s autorom Vladimiro Wagnerom, nech vam predlozi vlastne videnie nasich rieseni.
Re: Re: Bilancia
Pavel Brož,2017-08-21 15:19:43
Pane Nováku, bohužel jste naprosto nepochopil funkci těch navijáků k tomu lanu z geostacionární dráhy dolů a na druhou stranu k tomu protizávaží. Pokud popustíte naviják směrem k protizávaží, to se začne pomalu vzdalovat, těžiště toho systému (kotveného u zemského povrchu) se tím posune dále od Země, a vznikne tím přebytek tahu směrem nahoru, bez potřeby raketového motoru u protizávaží. Jakmile se výtahová kabina vyšplhá na geostacionární dráhu, lze díky těm navijákům a kotvení opět pomalu dorovnat vzdálenost protizávaží od geostacionární dráhy do původní polohy. Budete na to potřebovat energii do motoru toho navijáku, tu tam můžete přinést např. uskladněnou v baterii ve výtahové kabině, anebo pokud se podaří udělat lano vodivé, tak přímo elektrickým proudem ze zemského povrchu.
Manipulacemi s protizávažím a s vynášeným nákladem se sice dočasně ztratí geostacionarita, takže ve výsledku bude protizávaží vykonávat jakoby kyvadlové pohyby z východu na západ a naopak, ale to všechno se dá ukočírovat vhodnou synchronizací toho vynášení.
Tak jako tak ale žádné dodatečné tažení toho protizávaží pomocí raketových motorů nebude ke kompenzaci toho vynášeného nákladu potřeba, od toho tam budou ty navijáky. Pokud vaše společnost nezaměstnává kromě Vás osobně také inženýry, kteří jsou schopni princip těch navijáků pochopit, tak bych se osobně služeb vaší společnosti obloukem vyhnul.
Re: Re: Re: Bilancia
Miroslav Novak,2017-08-21 16:47:59
Pan Broz, je len vasou volbou ton, ktory ste nasadil.
Mna len fascinuje, ze dokazete ignorovat minimalne dva z troch Newtonovych zakonov v tak kratkom prispevku.
Takze ak ma tazne lano mat nejaku pevnost, predpokladame, ze sila, ktorou bude lano ukotvene o Zemegulu, musi byt co najmensia, ze?
Dalej, protizavazie je nejake teleso nenulovej hmotnosti majucej nezanedbatelnu obvodovu rychlost. Uz len vzorec 1/2 mv^2 na nieco ukazuje, ze ked zmenim navijakom co i len o milimeter radius rotacie tohoto telesa, bude sa jednat o vyznamny energeticky pocin.
Ak ale mate vo svojich uvahach, ze cely ten system bude vyzadovat navijak s vykonom porovnatelnym s raketovym motorom Saturnu, potom sa tohoto riesenia nedockame nikdy, ze?
Nutnost silneho navijaku znamena, ze odstrediva sila protizavazia je prilis velka.
Mala odstrediva sila znamena, ze nam zariadne spadne na navijak.
Takze vysledok je, ze na ten vas navijak treba, aby ta odstrediva sila bola vybalancovana na nulu.
Dalej, predstavte si dve lodky na vode. V jednej ste Vy a v druhej ja a drzime spolu lano.
Skuste mi vysvetlit, ako sa dokazete ku mne pritiahnut, aby sa moja lodka nepohla z miesta?
Dakujem vopred za odpoved.
Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-21 19:35:54
Takže - lano o požadované pevnosti cca 100 GPa by při celkové své hmotnosti kolem 750 tun mělo být schopno zvedat kabinu o hmotnosti cca 20 tun, viz např. zde: https://en.wikipedia.org/wiki/Space_elevator#Construction . 750 tun není nic, co by se nedalo už dnes zvednout či udržet na dostatečně silných navijácích. Pokud počítáme jenom s odstředivou silou působící na protizávaží (gravitační síla nám ty výsledky ještě zlepší), tak pokud budeme mít vyvažovací lano dlouhé jen 1200 km (tedy cca 1/30 délky lana směrem k povrchu), tedy o hmotnosti zhruba 25 tun, tak bude potřeba protizávaží o hmotnosti 725 tun (neuvažujeme teď gravitaci působící i na protizávaží, která nám to ještě vylepší). V této konfiguraci bude sestava v rovnováze, kdy odstředivá síla působící na protizávaží bude přesně vyvažovat tíhu lana pod geostacionární drahou.
Nyní budeme chtít připojit tu kabinu o hmotnosti 20 tun, nově tedy budeme potřebovat vyvažovat 770 tun místo 750. O kolik musíme odvinout lano k protizávaží, aby nám nárůst odstředivé síly vyrovnal těch 20 tun navíc? Jelikož odstředivá síla je při konstantní úhlové rychlosti a konstantní hmotnosti úměrná poloměru, tak potřebujeme poloměr zvětšit na 770/750 = 1,027, tedy z poloměru 35800 km + 1200 km = 37000 km na poloměr 1,027x37000 = 38000 km. Jinými slovy, na vyvážení dodatečně navěšené dvacetitunové kabiny bude zapotřebí odmotat 1000 km lana k protizávaží. Pokud bychom lano zatížili jenom dvaceti kilogramy, vyvážíme je odmotáním jednoho kilometru lana, a odmotáním jednoho metru lana vyvážíme zátěž dvaceti gramů.
Odmotání lana o milimetr jak popisujete tedy umožní vybalancování s přesností dvaceti miligramů, jinými slovy, ten systém bude velice snadno a přitom velice precizně řiditelný. Vybalancování těch sil tedy rozhodně nebude žádný problém. Na přitažení lana zpět bude zapotřebí energie řádově srovnatelné s tou, jaká bude potřeba k vynesení toho nákladu nahoru, ale s tím se samozřejmě počítá. Zvětšování rotační energie protizávaží jde na vrub neznatelnému zpomalení rotace při odvinutí lana, při jeho přitažení se rotace Země opět o stejný neznatelný kousek zrychlí.
Na vynesení dvacetitunové kabiny z povrchu Země na geostacionární dráhu bude zapotřebí vynaložit energii cca bilión Joulů, tedy cca 300 MWh. Při zavěšení kabiny bude potřeba popustit to lano o těch 1000 km, a po jejím odepnutí nahoře (nebo vyprázdnění, pokud zanedbáme hmotnost prázdné kabiny vůči nákladu) bude zapotřebí to lano s protizávažím opět stáhnout nazpět, na což padne dalších 2250 MWh, tedy na jeden cyklus potřebný pro vynesení nákladu 20 tun nahoru bude zapotřebí 2550 MWh, což činí 127 kWh na kg užitečné hmotnosti.
Jo a mimochodem ten Váš příměr s loďkou je naprosto mimo, u toho výtahu totiž hraje podstatnou, zdůrazňuji podstatnou roli ta odstředivá síla a to kotvení u zemského povrchu, nic takového ve Vašem nepodařeném příměru není.
Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-21 20:28:21
Pan Broz, musim Vas pochvalit, ze ste mi matematicky popisal zakon akcie a reakcie pri prenose nakladu na obeznu drahu aj s vynalozenou energiou.
Este Vam ale chyba, aby ste pochopil zakon zachovania energie, ked uz tak sibrinkujete s tym protizavazim o 1000 km hore dolu.
Operujete totiz s energiou, ktoru dodate protizavaziu na zaciatku projektu. S energiou nutnou na:
- vynesenie protizavazia na danu orbitalnu drahu a
- na udelenie rychlosti v smere orbitalnej drahy, plus
- pocitate s tym, ze protizavazie bude mat nejaku extra energiu navyse, aby posobila dostatocnou silu na tah lana Vami spominanych 725-750 ton.
Pocas vynasania nakladu po lane korigujete dlzkou lana orbitalnu drahu protizavazia o 1000 km. Kedze sa zmensi polomer otacania a obvodova rychlost zostane rovnaka, uhlova rychlost protizavazia stupne. To nam prispeje k tomu, ze protizavazie udeli nakladu horizantalnu zlozku rychlosti (vertikalne ma byt naklad vynasany svojpomocne).
Lenze udelit nakladu horizontalnu rychlost znamena, ze protizavazie samotne pride o cast svojej energie. Ta sa prejavi tak, ze klesne jej uhlova rychlost na povodnu uhlovu rychlost, ale pozor, uz na orbitalnej drahe o 1000 km nizsie.
Ked po vyneseni nakladu povolime lano naspat o 1000 km, protizavazie odstredivou silou prejde na originalnu orbitalnu drahu, ale s povodnou rychlostou, takze jej uhlova rychlost uz nebude taka, ako na zaciatku prepravy. Zobral ste jej energiu a tu jej musite vratit.
Ano, na niekolko doprav nakladu to moze stacit, ale nie vecne.
Lebo zakon zachovania energie, ze?
Preto som v prvom prispevku uviedol, ze treba mat tam hore nejaky zdroj energie...
Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-22 01:33:53
Ne, to jste bohužel pochopil nepřesně. To odvíjení lana tam není v průběhu vynášení nákladu, ale hned v průběhu zavěšování kabiny anebo hned po něm. Ideální by bylo, kdyby se zavěšování kabiny provádělo tak pomalu, aby se během něj stihlo odvinout těch 1000 km lana k protizávaží. V praxi by takto pomalé zavěšování kabiny na lano bylo krajně nepraktické, a navíc i částečně zbytečné kvůli elasticitě lana. Elastická tahová vlna se totiž bude po laně šířit rychlostí šíření zvuku v tomto materiálu – pokud bychom uvažovali, že rychlost šíření zvuku v grafenových nanotrubičkách by byla podobná jako rychlost šíření zvuku dejme tomu v oceli, tj. nějakých 5km/s, tak by se geostacionární stanice „dozvěděla“ o zavěšení kabiny až za zhruba dvě hodiny, protože teprve potom by k ní dorazila elastická tahová vlna.
Cílem toho odvíjení lana k protizávaží je obnovit bilanci sil působících na místě geostacionární stanice. Ideální totiž je, aby v tomto místě byly síly v rovnováze, přesněji řečeno jenom s malým tahovým přebytkem, který stíhá být kompenzován silou ukotvení lana na zemském povrchu.
Předpokládejme, že nosnost lana bude těch 20 tun užitečného nákladu, s patnáctiprocentní toleranční rezervou (ve skutečnosti se u kosmického výtahu předpokládá poměr mezi maximálním a provozním zatížením kolem dvou, ale to by likvidovalo to lano, počítejme proto těch patnáct procent jako provozní toleranci). Na začátku mějme nezatížené lano, teda s odpojenou nebo prázdnou kabinou. Předpokládejme, že přebytek tahu vzhůru budou tři tuny, jinými slovo, nezatížený výtah bude tahat za kotvu toho lana silou cca třiceti tisíc Newtonů. Pokud bychom nyní na lano zavěsili kabinu o hmotnosti 20 tun (nebo alternativně naložili prázdnou kabinu odpovídajícím nákladem), tak by se bilance sil změnila takovým způsobem, že by celá sestava zahájila jednoznačný pohyb dolů místo vzhůru, což by bylo jaksi nemilé. Proto je nezbytné současně s tím zatěžováním anebo krátce po něm (ideálně do těch dvou hodin, než se to zatížení propracuje po laně až ke geostacionární stanici).
Podívejme se, za jak rychle se lano s protizávažím stihne bez brzdění (tj. na volnoběh) rozvinout ze vzdálenosti 1200 km nad geostacionární drahou do vzdálenosti 2200 km nad ní, tedy ze vzdálenosti 43371 km od středu Země do vzdálenosti 44371 km od středu Země. Pokud to protizávaží na laně pustíme na volnoběh, bude pokračovat rovnoměrně přímočaře rychlostí rovnou své původní obvodové rychlosti, které je ve vzdálenosti 43371 km od středu Země rovna 11374 km/h. S pomocí středoškolské trigonometrie zjistíme, že po uražení 9367 km „volného letu“ se bude protizávaží nacházet právě o tisíc km dál od středu Země než původně, tedy v požadované vzdálenosti 44371 km od středu Země. Tuto vzdálenost 9367 km protizávaží urazí za 9367/11374 hodiny, tedy za necelých padesát minut. Jinými slovy, pokud bychom lano s protizávažím nechali odvíjet na volnoběh, pak by se za těch padesát minut dostalo o požadovaných 1000 km dále. My ale chceme to lano brzdit, budeme ho tedy brzdit takovou silou, aby se do požadované vzdálenosti dostalo až za ty dvě hodiny, kdy k nám od zemského povrchu právě dorazí ta elastická tahová vlna způsobená zavěšením dvacetitunové kabiny.
Takže zavěsíme kabinu a současně začneme nahoře s přibrzďováním pouštět to lano s protizávažím tak, aby za dvě hodiny bylo to protizávaží o 1000 km dále. Kabina se celou tu dobu vůbec nemusí hýbat, stačí, když bude ty dvě hodiny zavěšená v klidu (ve skutečnosti už může začít stoupat, za ty dvě hodiny stejně stihne urazit jenom cca pět procent z cesty ke geostacionární stanici, ale nekomplikujme to a nechme ji v klidu). Cílem toho prodloužení lana k protizávaží ve skutečnosti je, aby celý systém zůstal v silové rovnováze, tedy aby v důsledku zavěšení dvacetitunové kabiny nezačal jako celek padat dolů.
Samozřejmě by se to dalo řešit i tak, že by žádné odvíjení lana k protizávaží nebylo potřeba, pokud by nezatížený výtah působil na kotvu silou větší než je síla odpovídající tíze 20 tun. Pak by samozřejmě dodatečné zatížení lana dvacetitunovou kabinou žádný sestup celé sestavy dolů nezpůsobilo, naopak ten systém by byl i poté v rovnováze. Jenže by to bylo plýtvání drahocennou nosností lana, které by nyní muselo disponovat provozní nosností 40 tun místo dřívějších dvaceti. A to jenom proto, aby po většinu času, kdy je výtah nezatížený, na něm byl generován ten dvacetitunový přebytek tahu ukotvený na zemském povrchu. My ale budeme nosností lana šetřit a budeme mít jen třítunový přebytek tahu, a těch dvacet tun kabiny vykompenzujeme hned po jejím zavěšení zvětšením délky lana k protizávaží.
V okamžiku, kdy se ta dvacetitunová kabina začne šplhat vzhůru, tak už bychom optimálně měli mít ty síly opět vyvážené. Během těch 36 hodin stoupání kabiny budeme muset to protizávaží zase naopak začít přitahovat, a to protože tíha té kabiny bude postupně klesat s tím, jak se bude blížit ke geostacionární dráze – v místě geostacionární dráhy už bude tíha té kabiny nulová (pokud to někomu zní divně, měl by si vzpomenout, že tíha nerovná se pouze gravitační síla, ale gravitační síla minus odstředivá síla, a tyto dvě síly působící na stoupající kabinu se právě na geostacionární dráze vyrovnají). Takže během cca 36 hodin stoupání bychom měli zase postupně přitahovat to protizávaží tak, abychom v okamžiku, kdy kabina dorazí na geostacionární dráhu, měli protizávaží přesně ve vzdálenosti, v jaké bylo před zavěšením kabiny dole, tj. opět pouhých 1200 km od geostacionární stanice.
Proto ty etapy budou vypadat takto:
a) ještě nezavěšená kabina dole na zemském povrchu, protizávaží 1200 km nad geostacionární stanicí. Na kotvu lana na zemském povrchu působí malý efektivně třítunový přebytek tahu;
b) zavěšení dvacetitunové kabiny na lano, během dvou hodin brzděné odvíjení lana s protizávažím, které se za ty dvě hodiny vzdálí do vzdálenosti 2200 km od geostacionární stanice. Po skončení tohoto manévru budou opět síly působící na geostacionární stanici v rovnováze, tj. odstředivá síla protizávaží bude zvětšena přesně tak, aby kompenzovala těch dvacet tun na laně navíc;
c) stoupání kabiny nahoru ke geostacionární stanici, což zabere těch 36 hodin za předpokladu rychlosti stoupání 1000 km/h. Během této doby se bude opět pomalu navíjet to lano k protizávaží tak, aby v okamžiku, kdy kabina dorazí do geostacionární stanice, bylo protizávaží opět ve vzdálenosti 1200 km nad stanicí.
Celý proces je časově reverzibilní, tzn. jde postupovat od bodu c) zpětně k bodu a) časovým obrácením všech dílčích kroků.
Je důležité si také uvědomit, že v případě jednosměrného vynášení nákladu od zemského povrchu nahoru je bodem c) už uzavřen jeden celý cyklus. Je to proto, že tíha té kabiny je na geostacionární stanici nulová, proto se tam jejím odpojením od lana žádná silová rovnováha nezmění. Ta kabina se tam zkrátka může odpojit a nechat poslat dále do vesmíru, výtah je každopádně už na konci bodu c) v identickém stavu, jako v bodě a), tzn. je možné dole připojit další dvacetitunovou kabinu a body b) a c) opakovat do nekonečna. Kabiny se v tomto případě nerecyklují, dole se prostě zavěšují stále nové. Samozřejmě v praxi bude mnohem rozumnější udělat něco na způsob vlaků metra – připojitelné a odpojitelné kabiny budou jezdit zdola nahoru a shora dolů jako vlaky na nějaké trase metra, přičemž na obou koncích, tj. na zemském povrchu a na geostacionární stanici budou depa s momentálně stojícími kabinami, které budou průběžně kontrolovány, než budou vpuštěny na další cestu. V případě potřeby bude ale možné krátkodobě poslat několik kabinek po sobě pouze jedním směrem – ostatně z metra během výluk to známe také.
Takže takhle je to s tím povolováním lan k protizávaží, nikoliv tak, jak jste napsal Vy. Co se týče toho rozkmitávání v horizontálním směru, to jsem rozepsal už v jiném dřívějším příspěvku, popíšu to nyní podrobněji. Při odvinutí lana k protizávaží o 1000 km toto protizávaží zaostane za geostacionární stanicí o malý úhel 0,187 stupně měřeno ze středu Země, tedy o cca 11 úhlových minut. Resp. o tento úhel by to protizávaží zaostalo, pokud by to odvíjení jelo na volnoběh, my předpokládáme, že bude brzděné, takže ten úhel bude ve skutečnosti menší. Tak jako tak ale vzniknou horizontální oscilace. V místě geostacionární stanice bude úhel mezi lanem směrem dolů a lanem k protizávaží nově 176,42 stupně místo původních 180 stupňů – jinými slovy, v důsledku popuštění toho lana k protizávaží se v místě geostacionární stanice změní původní přímka v lomenou úsečku s „úhlem nalomení“ 3,58 stupně.
Je nutné zdůraznit, že i když dojde k horizontálním oscilacím protizávaží, v žádném případě nedojde k nějaké katastrofě typu začátek pádu geostacionární stanice, protože k vyrovnání tohoto efektu stačí velice malý přebytek tahu toho protizávaží. Předpokládáme, že to protizávaží vyrovnává tíhu toho hlavního lana o hmotnosti cca 750 tun (jak už víme, tíha toho lana sice bude menší než ekvivalent těch 750 tun kvůli tomu, že na vyšší části lana bude působit menší gravitace plus bude na ně působit opačně orientovaná odstředivá síla, nicméně to je v těchto úvahách podružné, naopak by to pro nás vyšlo ještě lépe). Dá se ukázat, že pokud bude na geostacionární stanici působit pouhý třítunový přebytek tahu (jinými slovy, nastavíme délku lan k protizávaží tak, aby kompenzovalo kromě 750 hmotnosti hlavního lana směrem k Zemi ještě 3 tuny navíc, které budou kompenzovány kotvou na zemském povrchu), tak i po vzniku úhlové odchylky 3,58 stupně mezi lany v místě geostacionární stanice bude po rozkladu sil výsledná síla působit směrem NAD, nikoliv POD geostacionární dráhu. Třítunový přebytek tahu nám tedy bude garantovat potřebnou stabilitu stanice na geostacionární dráze, která i když bude maličko zpomalená dozadu vychýleným protizávažím, tak stejně bude díky přebytku toho tahu nadále tažena směrem NAD dráhu, tedy nezačne padat pod ní.
Přebytek toho tahu tedy způsobí, že stanice se udrží na své dráze i přes dočasné zpomalení, protože ztrátu její kinetické energie vykompenzuje přebytečný tah protizávaží. Tento přebytek způsobí to, že se stanice dočasně zpomalí, ovšem naopak zrychlí to protizávaží, takže jejich role se po nějaké době obrátí. Vzniknou oscilace podobné jako u dvojitého kyvadla, matematicky se dá dokonce dokázat, že popis obou bude velice podobný – stačí, když si představíme Zemi jako hlavní bod závěsu toho dvojitého kyvadla, z tohoto bodu visí první kyvadlo, které končí ve vzdálenosti geostacionární dráhy, a z toho prvního kyvadla visí druhé kyvadlo (protizávaží). Rozdíl bude pouze v tom, že u dvojitého kyvadla působí na obě homogenní síla v pevně daném směru, zatímco v našem případě ta síla bude daná odstředivou silou a tedy nebude v pevně daném směru. Pro malé kmity (a to je náš případ, viz odchylka 3,58 stupně) bude ale rozdíl mezi oběma systémy velmi malý.
Výsledkem vzájemného silového působení mezi geostacionární stanicí, kotvenou lanem k Zemi, a protizávažím, táhnoucím ji díky třítunovému přebytku tahu vždy nad geostacionární dráhu, budou tedy horizontální kmity, kdy podobně jako u dvojitého kyvadla se budou geostacionární stanice a protizávaží střídavě předbíhat a zpožďovat. Toto předbíhání a zpožďování bude energeticky konzervativní proces, tzn. nebude k němu zapotřebí dodávat energii, podobně, jako u dvojitého kyvadla, pokud u něj zanedbáme tření (a to ve vakuu opravdu zanedbat můžeme).
Takže toto je odpověď na Vaši námitku ohledně zákonu zachování energie. Zákon zachování energie nebude narušen, v průběhu odvíjení lana pouze dojde k úhlovému zpoždění toho protizávaží za geostacionární stanicí, načež dojde ke vzniku kmitů analogických kmitům dvojitého kyvadla. Stanice a protizávaží začnou horizontálně kmitat, jejich poloha bude v průměru úhlově zpožděná o konstantní úhel oproti výchozímu stavu. Třítunový přebytek tahu bude garantovat stabilitu stanice, která díky němu ani při dočasně snížené rychlosti neklesne pod geostacionární dráhu, protože díky tomu přebytku bude výslednice sil působící na stanici mířit vždy nad tuto dráhu. Při vhodně (zdůrazňuji vhodně) synchronizovaném přitahování protizávaží navíc půjde obnovit původní statický stav, kdy stanice bude mít nulovou úhlovou odchylku od své původní polohy a kdy úhel mezi oběma lany bude opět konstantních 180 stupňů a nebude se měnit (opět až do začátku dalších manipulací s lanem).
Mimochodem, u té manipulace s lanem jsem tu energii potřebnou k zpětnému přitažení protizávaží původně započítal do oněch výsledných 127 kWh na kg užitečné hmotnosti. Tuto energii v článku takto nezapočítávají, tam vychází pouhých 14,8 kWh/kg, a pro to nezapočítání existuje dobrý důvod. Ta energie potřebná ke zpětnému navíjení lan se totiž dá akumulovat už při jejich odvíjení, např. roztáčením setrvačníků. Vlastně tak vytvoříme něco jako kosmické jojo, kdy při odvíjení lana jeho brzděním roztočíme pomocný setrvačník, který pak necháme běžet na volno (odpojený od lana) až do doby, kdy to protizávaží budeme potřebovat znovu přitáhnout, pak pouze nějakým převodovkovým mechanismem připojíme to lano na roztočený setrvačník a necháme ho znovu přitáhnout, čímž zase odebereme rotační energii tomu setrvačníku. Nejde to samozřejmě dělat se stoprocentní účinností, nicméně v podmínkách vakua a beztíže se lze těm ideálním stům procentům přiblížit na více než devadesát devět procent.
Suma sumárum, nahoře žádný enormní zdroj energie, a už vůbec ne v podobě raketových motorů není vůbec zapotřebí. Všechno je jenom optimálně využitá klasická mechanika, výsledné kmity jsou podobné kmitům dvojitého kyvadla, průměrná úhlová odchylka stanice při popuštění lana vznikne, nicméně při jejich optimálně synchronizovaném přitažení bude zase eliminována. Energie potřebná k přitažení se dá získat rekuperací při odvíjení např. s využitím setrvačníků. Pouhý třítunový přebytek tahu u lana hmotného 750 tun garantuje stabilitu stanice na geostacionární dráze i přes dočasné zpomalení stanice, protože výslednice sil bude díky tomu přebytku stále mířit nad tu dráhu. Jedinou nevratnou energii budete potřebovat k vynesení té kabiny nahoru, to je těch mnou uvedených 300MWh na dvacetitunovou kabinu, tedy 15 kWh/kg (v článku uvedených přesněji jako 14,8 kWh/kg). Energie potřebná ke stabilizaci té soustavy pomocí přitahování a odvíjení lan se dá oproti tomu s velkou účinností rekuperovat.
Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 08:54:48
Pan Broz, Vas to musi strasne bavit opisovat silove pomery. Zrejme tym chcete nieco zakryt. Asi to, ze ja sa bavim o energi, ktorej ste venoval posledne dva odstavce, pricom ten druhy ste len opisal z predosleho prispevku. Dobry pokus, ale nedostatocny.
Vas primer k jo-jo systemu naozaj myslite vazne? To chcete tvrdit, ze ked spustim jo-jo, tak sa bude kmitat do nekonecna? Vy mate radi perpetuum mobile?
Skuste teraz odpisat prispevkom s 2 milion slovami, cim este viac potvrdite svoju neochotu najst mi tu energiu, ktora sa vo vasom projekte jednoducho straca. Proste ignorujete Newtonove zakony, aj ked ked Vase nadsenie je nebotycne.
Myslim, ze aj pan Pospisil velmi dobre argumentuje vytvaranim tetivy a pan Wagner tiez tapa ako ziacik, ktoreho ucitel prichytil pri nezrovnalostiach. Pan Broz, chovate s panom Wagnerom, ako by ste obhajovali svoje dielo, pricom to nie je pravda. Preco sa staviate do takej smiesnej ulohy?
Ked tak citam tu Vasu poslednu vetu, tak toto zariadenie by sa dalo nazvat tiez ako takmer nekonecny zdroj energie. Rekuperaciou by ste mohli vyrabat energiu tym, ze popustite navijak. Lenze pritahovanim lana energiu nevyrobite, tak by to bol vlastne zasobnik energie. Momentalne prebytocnu elektrinu by ste pouzil na pritahovanie protizavazia.
Ale kedze cele je to energeticky nevybalansovane, je to nezmysel uz aj ako vesmirny vytah.
Nuka sa mi parafrazovat nasu byvalu premierku: 16 vedcov sa predsa nemoze mylit.
Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 10:34:32
Pan Broz, cim dlhsie citam tu Vasu poslednu vetu, tym viac som presvedceny, ze ste sa stal obetou vlastnej fantazie v zmysle, ze ak:
- pred geostacionarnym orbitom posobi gravitacna sila Zeme,
- na geostacionarnej drahe je gravitacna sila nulova, tak
- za geostacionarnou drahou posobi "nejaka" sila odstrediva od Zeme.
V takomto obraze je potom velmi lahke podlahnut iluzii, ze potom staci popotahovat zo zeme lanom a mame vybudovane energeticke cerpadlo. V kazdom smere potiahnem lanom a stale mi to vytvara energiu. Potiahnutim k sebe pomaham vynasat naklad, povolenim od seba dodavam naspat energiu protizavaziu (mozno je to vo Vasich uvahach naopak, ale na principe sa nic nemeni).
V odpovedi na pana Wagnera som dal malu anketu, skuste ju zodpovedat, aby sme videli, ake predstavy mate Vy. Dakujem vopred.
Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Vladimír Wagner,2017-08-22 10:58:57
Pane Nováku, jediné co pan Brož a správně předpokládá, je, že při dané úhlové rychlosti systému jsou na geostacionární dráze gravitační a odstředivá síla vyrovnané, před geostacionární dráhou gravitační síla převládá a nad geostacionární dráhou pak je větší odstředivá síla než gravitační.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 11:10:38
a to je, pan Wagner, strasne malo. Skuste v kroatkosti odpovedat, co je zdrojom sily nad geostacionární dráhou? Dakujem vopred za odpoved.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-22 14:51:05
Pane Nováku, odpovím za pana Wagnera - zdrojem odstředivé síly je zde rotující souřadná soustava. Račte si laskavě Newtonovy zákony přepsat z inerciální soustavy do soustavy rotující, a ta odstředivá síla tam automaticky vznikne jako důsledek volby té neinerciální rotující soustavy. Jak vidím, tak ze zkoušky z klasické mechaniky byste propadl už v prvním semestru, když nevíte, že v rotující soustavě efektivně vzniká odstředivá síla, a že zdrojem této síly je právě rotace té soustavy.
Odstředivou sílu lze samozřejmě popsat i v inerciální nerotující soustavě, tam ji dostaneme jako důsledek rotačního pohybu tělesa vůči té nerotující soustavě ze vztahu F = m r omega^2, kde omega je úhlová rychlost tělesa vůči té soustavě. V rotující souřadné soustavě, vůči níž se ale těleso nepohybuje, ale nemůžeme použít úhlovou rychlost tělesa vůči soustavě. V neinerciální soustavě ale působí navíc zrychlení mající původ právě v té neinerciálnosti soustavy, v rotující soustavě je toto zrychlení rovno r omega^2, kde omega je úhlová rychlost rotace soustavy vůči inerciálnímu framu. Jinými slovy v neinerciálních soustavách neplatí první Newtonův zákon, protože na těleso, které je v těchto soustavách v klidu, přesto působí nenulové síly. V případě rotující neinerciální soustavy je touto silou síla stejná, jakou dostanete v té inerciální soustavě. Toto je ale obsahem učiva prvního semestru klasické mechaniky, který jste zřejmě prospal, pokud jste ho vůbec navštěvoval.
Co se týče té energetické bilance, tak ta se samozřejmě nenarušuje, o perputuu mobile tady plácáte jenom Vy. Soustava Země, obě lana, geostacionární stanici, setrvačník a protizávaží je samozřejmě uvažována jako uzavřená soustava, v níž se zachovávají jak zákon zachování hybnosti, tak zákon zachování energie. Samozřejmě že je nutné tím pádem uvažovat všechny složky hybnosti a energie, které tam vstupují do bilance, vynecháním kterékoliv z nich snadno vznikne chyba. Takže v potaz je nutné vzít translační i rotační kinetickou energii Země, kinetickou a potenciální energii stanice, kinetickou a potenciální energii protizávaží, a rotační energii setrvačníku (pokud je spojený s geostacionární stanicí, tak jeho kinetickou a potenciální energii můžeme započíst do kinetické a potenciální energie té stanice). Celý proces odmotávání lana se dá rozfázovat do jednotlivých fází, kdy dochází k předávání hybností a energií vždy mezi dvěma sousedními prvky té sestavy, vždy tak, že v každém kroku bude splněn jak zákon zachování hybnosti, tak zákon zachování energie. Mám to ale dělat? Má to vůbec smysl, když máte problém s původem odstředivé síly v rotující soustavě? Klidně to rozepíšu, jenže Vy tomu nebudete rozumět a budete si pak zase stěžovat že je to dlouhé a do toho plácat nesmysly o perpetuu mobile, které tam ve skutečnosti nikde nevzniká.
Jo a mimochodem, to, že jsem věnoval tak velkou pozornost těm silovým bilancím, to má ten důvod v tom, že právě teprve na základě silových bilancí získáte geometrie těch konfigurací, jako např. různé úhly atd., což na základě energetických bilancí samozřejmě získat nelze, ovšem to by Vám - pokud byste ho ovšem absolvoval - mělo být už po prvním semestru vysokoškolské fyziky taky jasné.
Takže mám to rozepsat, krok po kroku, budete to vůbec ochoten přečíst?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 15:13:15
Pan Broz, mate pravdu, neviem citat a inercialne sustavy su pre mna spanielska dedina.
Kedze som mselej iteligencie, dokazali by ste mi odpovedat na jednoduchu otazku, ktoru som uz polozil aj inde?
Predstavte si, ze dame na obeznu drahu predmetne protizavazie aj s lanom.
Vsetko pred vynesenim prveho nakladu funguje naprosto synchronizovane.
Otazka znie: "Ako dlho tento system vydrzi letiet po orbitalnej drahe, nez vynesieme prvy naklad bez akykolvek korekcii drahy protizavazia a lana?"
Navrhovane anketove odpovede su:
a) 1 mesiac,
b) 1 rok, alebo
c) 1 storocie?
Viete svoju odpoved aj vyargumentovat?
Neskusajte vlozit odpoved d) věčně.
Dakujem vopred za odpoved co sa vojde na jednu obrazovku.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 15:41:24
Pan Broz, je zaujimave, ze ste prave tu finalnu cast, ako pisete: "Celý proces odmotávání lana se dá rozfázovat do jednotlivých fází, kdy dochází k předávání hybností a energií vždy mezi dvěma sousedními prvky té sestavy, vždy tak, že v každém kroku bude splněn jak zákon zachování hybnosti, tak zákon zachování energie", ze prave tuto cast nechcete rozpisat.
Prave tu cast, ktora ma zaujima od zaciatku a nie tie doprovodne silove pomery okolo.
Mna totiz nezaujima, ci ma moje auto tolko alebo tolko Nm, ako sa prenasa sila z valca cez klukovu hriadel, prevodovku az na kolesa.
Mna zaujima, ci mam dost benzinu, aby ma auto dopravilo do cielovej stanice.
Ci to protizavazie dokaze kompenzovat energeticke straty vznikajuce pri doprave nakladu hore.
Energetickej bilancie sa bojite. Ale vyhovarate sa na to, ze by som to nebodaj nepochopil, alebo, najnovsie, ze to neviem ani precitat.
Pretoze dojdete k zaveru, ze to protizavazie je treba "dobijat" o stratenu energiu pri doprave,
podobne ako je treba protizavazie dobijat o straty pri rotacii, aj ked nebude vykonavat ziadnu uzitocnu pracu v podobe dopravy nakladu na orbitalnu drahu.
Len smelo, pan Broz, sustredte sa najma na tu jalovu cast pribehu, aby ste nemusel vytvarat umelecke diela, ze system pracuje iba vtedy, ked vynasa naklad, ale pri prevadzkovom klude to akosi nefunguje.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 15:53:41
Alebo bude stacit, ked odpoviete na nasledujuce otazky:
- co uvedie suradnu sustavu do rotacie? (jednoducha otazka)
- co udrzuje rotujucu suradnu sustavu v synchronnej rotacii, zhodnej uhlovej rychlosti Zeme a protizavazia? (otazka, na ktoru sa zrejme odpovede nedockam)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Jiri Matus,2017-08-22 18:19:41
Pokusím se odpovědět za trpělivé pány Brože a Wagnera ;-)
Co uvede soustavu (Země a družice) do rotace?
- Země ... již rotuje
- družici + lana + protizávaží uvede do (synchronní) rotace na geostacionární dráze samozřejmě klasický raketový motor
Co udržuje shodnou úhlovou rychlost Země a protizávaží?
- odstředivá síla protizávaží (a lana za geostacionární drahou) protože:
protizávaží (a celá soustava) se při vynášení nákladu vychýlí, to ano, ale výchylka od přímky způsobí rozklad odstředivé síly na horizontální a vertikální složku a ta horizontální bude soustavu vracet zase do té stabilní "přímky" . Musí ovšem být vyvíjen nenulový tah na to ukotvení na zemi, protizávží musí být tak daleko aby neustále napínalo lano tj. trochu i tahalo za ten kotvící systém, ale né moc, aby se nepřetrhlo lano (a to se právě reguluje tím navijákem)
A tímto taháním za ten kotvící kolík (při vynášení trošku i v horizontálním směru proti rotaci Země) se právě rotace Země (neměřitelně) zpomalí, a to je asi ta energie na kterou se ptáte.-
- třeba když si točíte s matkou (protizávaží) na provázku a od prstu (kotvící systém) pošlete po provázku další (jen do půlky, kde je uzel = stanice s navijáky) tak se to rozkmitá, ale pak se to zase ustálí.
Nečetl jsem celou diskuzi, možná už to tam v jiné formě zaznělo.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Jiri Matus,2017-08-22 18:46:59
Tou přímkou v příspěvku výše myslím přímku - střed/osa rotace Země - místo ukotvení na povrchu - protizávaží
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 19:46:14
Dobry vecer, pan Matus,
dakujem Vam za Vasu odpoved, pozorne som si ju precital a trpezlivo cakam, kedy niekto z vas konecne prekroci ten problematicky bod, o ktorom pisem.
Vsetci tu popisujete, ako budete nieco za nieco tahat, ale si neuvedumejete, ze tym pritiahnutim protizavazia pripravite to protizavazie o kineticku energiu, cim ju pripravite aj o moznost vyvolat povodne velku odstredivu silu. A tu jej kineticku energiu jej treba vratit.
Pan Broz mi "skoro" slubil, ze energeticku bilanciu, ako tomu protizavaziu naspat vrati kineticku energiu, popise fyzikalnymi vzorcami. Verim, ze mu to bude trvat dlhsie, nez sa spociatku dusoval. Keby nestracal cas urazanim diskutujuceho, ale predlozil bilanciu, to by bolo ine kafe.
Zatial sa mnohi hrate na demokraticku vedu. Skusate argumenty prehlasovat poctom nadsencov projektu vesmirneho vytahu. Viete, co povedal Einstein na pochybnosti stovky nemeckych vedcov o jeho teorii relativity?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-22 19:58:16
Pan Matis, k Vasmu experimentalnemu pokusu.
Skuste tento pokus urobit napriklad s kolesom od bicykla. Je dostatocne hmotne v porovnani s pouzitou dvojicou matiek.
Koleso upevnite vodorovne, priviazte na neho spagat s jednou maticou na konci a s druhou pri kolese a roztocte koleso tak, aby matka taktiez kruzila v rovine kolesa a nasledne pustite tu druhu maticu (pomocka: Koleso roztacajte v tom bode, kde je priviazany spagat a prichytena druha matica).
Pri dostatocne malej matici skriknete heureka, pretoze hybnost kolesa dokaze zvladnut zmenu hybnosti druhej matice (prejde do vacsieho radiusu a tym vyssej obvodovej rychlosti).
Pokus zopakujte s dostatocne tazkymi maticami, aby ta energeticka transformacia bola zjavna.
Uvidite, ze uz tie dve matice nikto nikdy nevrati do povodnej rovnovahy (aby spagat smeroval do osi kolesa), pokial bud:
- kolesu neudelite svojou rukou dodatocnu energiu, alebo
- alebo nezrychlite matice rucne...
Potom hlboko rozmyslajte nad tym, kde sudruhovia z NDR urobili chybu.
Sice ma uplacate capicami, ale mne to nevadi. Som mdleho rozumu a neviem citat.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-23 03:01:02
Pane Nováku, co se týče Vaší otázky, kotvený výtah stabilizovaný přebytkem tahu (pouze o takovém se bavíme) vydrží na oběžné dráze nejméně po dobu životnosti lana. Pokud lano přežije bez údržby rok, tak rok, pokud déle, tak déle. Nekotvený výtah, ale o takovém se nikde neuvažuje, by tam nevydržel bez řízení ani měsíc, protože ta poloha je nestabilní.
Nyní k těm jednotlivým krokům, ve kterých se budou předávat hybnost a energie mezi jednotlivými komponentami systému. Veličiny popisující geostacionární stanici označme indexem g (např. její obvodovou rychlost jako v_g, její vzdálenost od středu Země jako R_g, její hmotnost jako m_g), analogické veličiny pro protizávaží budou mít index p, tedy rychlost bude v_p, vzdálenost od středu Země R_p, hmotnost m_p. Pro veličiny popisující Zemi budeme používat index Z, pro setrvačník s. Za indexy g, p, Z nebo s budeme přidávat číslice označující postupné změny příslušných veličin (např. v_p_1, v_p_2 atd.), či označující radiální či tangenciální složky těchto veličin (např. v_p_2_r, v_p_2_t). Setrvačník bude umístěný na geostacionární stanici, jeho kinetická a potenciální energie bude zahrnuta v kinetické a potenciální energii stanici, takže pouze jeho rotační energii bude zapotřebí počítat separátně. Konstrukce setrvačníku bude v podobě dvou protiběžných setrvačníků, aby při jeho brzdění či roztáčení nedošlo k udělování rotace stanici. Popis budeme pro konkrétnost provádět v inerciální nerotující soustavě s počátkem souřadnic ve středu Země (tedy v této soustavě bude rotovat i Země).
Výchozí stav: střed Země, bod ukotvení lana na povrchu Země, geostacionární stanice a protizávaží jsou v přímce, a celý tento systém rotuje kolem středu Země úhlovou rychlostí omega_Z = 2pi/86400 = 7,272*10^-5 s^-1. Hmotnost Země M_Z= 5,972*10^24 kg, gravitační konstanta kappa=6,674*10^-11 m^3/(kg s^2). Lano je ukotvené ve vzdálenosti R_Z = 6378 km od středu Země, geostacionární stanice je ve vzdálenosti 35800 km nad povrchem Země, tedy ve vzdálenosti R_g = 42178 km od středu Země. Protizávaží bude o 1200 km dále, tedy ve vzdálenosti R_p_1 = 43378 km. Hmotnost protizávaží nechť je m_p = 750 tun, hmotnost geostacionární stanice nechť je m_g = 1000 tun. Oběžná rychlost stanice je v_g_1 = omega_Z R_g = 3,067 km/s, oběžná rychlost protizávaží je v_p_1 = omega_Z R_p_1 = 3,155 km/s. Kinetická energie geostacionární stanice je K_g_1= (1/2) m_g v_g_1^2 = 4,704 TJ, její potenciální energie je U_g=–kappa m_g M_Z/R_g = -9,450 TJ. Kinetická energie protizávaží je K_p_1=(1/2) m_p v_p_1^2 = 3,733 TJ, jeho potencionální energie U_p_1=–kappa m_p M_Z/R_p_1 = -6,891 TJ. Počáteční rotační energie K_s_1 setrvačníku nechť je nulová.
Krok 1: uvolníme naviják lana k protizávaží, zatím bez připojeného setrvačníku, který tedy zatím zůstává neroztočený. Protizávaží se po tečně vzdaluje, necháme ho vzdalovat až dokud nebude od středu Země o 1000 km dále. Jeho nová vzdálenost bude tedy R_p_2 = 44378 km od středu Země, jeho potenciální energie bude nyní U_p_2 = -kappa m_p M_Z/R_p_2 = -6,736 TJ, tedy zvýší se o (-6,736+6,891)=0,155 TJ, o tutéž energii se tedy sníží kinetická energie protizávaží, která bude nově K_p_2 = 3,578 TJ, rychlost protizávaží na nové pozici tedy bude v_p_2 = 3,089 km/s. Protože rychlost protizávaží v důsledku stoupání v gravitačním potenciálu Země klesla, a také v důsledku toho, že během této etapy se protizávaží nepohybovalo po kruhové dráze, protože naviják byl puštěn na volnoběh, bude protizávaží nyní úhlově zaostávat o 0,187° za geostacionární stanicí. Vůči počátku soustavy (připomínám, že jsme zvolili inerciální nerotující soustavu) během odvíjení opíše úhel alfa=12,187°. Nová rychlost v_p_2 nebude již plně tangenciální jako ve výchozím stavu, ale bude mít jak tangenciální, tak radiální složku – radiální složka rychlosti protizávaží bude rovna v_p_2_r = 0,33 km/s, zatímco tangenciální složka (tedy nová oběžná rychlost protizávaží) nyní bude v_p_2_t = 3,071 km/s.
V kroku 1 je stále zachovaná bilance energie, protože jediná energetická transformace, která v tomto kroku proběhla, bylo zvýšení potenciální energie protizávaží za současného snížení jeho kinetické energie o stejnou část. Všechny ostatní energie všech ostatních komponent systému zůstaly stejné, jako ve výchozím stavu, proto součet energií zůstane v kroku 1 stejný jako ve výchozím stavu.
Krok 2: protože rychlost protizávaží má nyní i malou radiální složku v_p_r2=0,33 km/s, tuto energii využijeme k roztočení setrvačníku. Při odvíjení posledních pár kilometrů z oněch popouštěných 1000 km zapřáhneme setrvačník vhodně zpřevodovaný tak, aby nám to lano na těch posledních pár kilometrech zastavil. Tím absorbujeme radiální rychlost toho protizávaží, takže nám nově zůstane pouze tangenciální složka: v_p_3 = v_p_2_t = 3,071 km/s. Část kinetické energie protizávaží odpovídající této radiální složce se tedy přemění na rotační energii setrvačníku, setrvačník tedy získá energii K_s = K_p_2_r = (1/2) m_p v_p_2_r^2 = 0,041 TJ. Připomínám, že jelikož jsou radiální a tangenciální složka rychlosti na sebe kolmé, tak kinetická energie K_p_2 je součtem kinetických energií odpovídajících radiální a tangenciální rychlosti, tedy K_p_2 = (1/2) m_p v_p_2_r^2 + (1/2) m_p v_p_2_t^2.
V kroku 2 zůstává opět zachována bilance energie, protože zde došlo opět pouze k přelití stejné části mezi radiální částí kinetické energie protizávaží a energií setrvačníku, a opět všechny ostatní energie zůstaly nedotčené.
Krok 3: Máme tedy protizávaží spuštěné o potřebných 1000 km, nyní opět obíhá tangenciálně jak potřebujeme, setrvačník se nyní točí a uchovává tak v sobě potřebnou energii na její pozdější vytěžení, ovšem tangenciální rychlost protizávaží je menší, než by měla být. Aby byl jeho pohyb synchronní s geostacionární stanicí, potřeboval by se pohybovat rychlostí omega_Z R_p_2 = 3,227 km/s, ovšem pohybuje se pouze rychlostí 3,071 km/s. Setrvačník už máme znova odpojený od navijáku, naviják máme zafixovaný. Začne se nám tudíž šponovat lano od protizávaží ke geostacionární stanici. Ne, nepraskne, tato síla není nijak radikálně větší, než byla původní odstředivá síla působící na to lano ve výchozím stavu, a koneckonců to lano už muselo přežít srovnatelnou sílu při absorbci radiální složky v předchozím kroku, která byla numericky dokonce ještě větší. Tento tah ale způsobí srovnání rychlostí mezi geostacionární stanicí a protizávažím. Po tomto srovnání budou mít geostacionární stanice i protizávaží stejnou úhlovou rychlost omega_g_2, která bude ale menší než úhlová rychlost obíhání Země. Novou úhlovou rychlost získáme z požadavku na konstantnost součtu kinetické energie stanice a protizávaží, z čehož nám vyjde:
omega_g_2 = odm[(m_g v_g_1^2 + m_p v_p_3^2)/(m_g R_g^2 + m_p R_p_2^2)] = 7,11*10^-5 s^-1
Tato úhlová rychlost je o 2,8 procenta menší než úhlová rychlost Země, a proto je už nyní jasné, co se stane v příštím kroku. Nová oběžná rychlost geostacionární stanice bude nyní v_g_2 = omega_g_2 R_g = 2,999 km/s, zatímco nová oběžná rychlost protizávaží bude nyní v_p_4 = omega_g_2 R_p_2 = 3,155 km/s.
V kroku 3 samozřejmě opět zůstává energetická bilance zachována, protože opět dojde jenom k vzájemnému předání stejné části mezi dvěma dílčími energiemi, zde kinetickou energií geostacionární stanice a kinetickou energií protizávaží. Všechny ostatní energie včetně té uložené v roztočeném setrvačníku zůstávají opět identické jako v předchozím kroku.
Krok 4: menší úhlová rychlost sestavy geostacionární stanice plus protizávaží samozřejmě způsobí šponování nyní toho hlavního lana směrem k Zemi. Země se točí rychleji než tato sestava, a tedy prostřednictvím toho lana urychlí sestavu geostacionární stanice plus protizávaží na synchronní úhlovou rychlost. To se samozřejmě odehraje na účet rotační energie Země, která se malilinko zpomalí – konkrétně půjde o prodloužení délky dne o 1,1*10^-18 dne, tedy o necelou desetinu bilióntiny (tj. 10^-13) sekundy. Ve výsledku budou opět tedy opět geostacionární stanice s protizávažím obíhat synchronně stejnou úhlovou rychlostí jako Země, tedy v podstatě jako ve výchozím stavu, pouze s tím, že protizávaží bude dočasně malilinko zpožděno za geostacionární stanicí o nepatrný úhel. Ve skutečnosti bude to protizávaží s geostacionární stanicí vykonávat velice pomalé horizontální kmity s úhlovou amplitudou nepřevyšující 0,187°, což bude na geostacionární dráze plus minus 137,7 km rovnovážné polohy. O vzniku těchto kmitů jsem se už ve svých dřívějších příspěvcích zmiňoval, stejně jako o tom, že při vhodně načasovaném opětovném přitažení toho protizávaží je opět možné obnovit původní nekmitající stav (samozřejmě že při nešikovně načasovaném přitažení se tyto horizontální kmity mohou naopak ještě zvýšit).
Ani v kroku 4 nedojde k žádnému narušení zákona zachování energie – energetická bilance zde bude opět identická, jako v předchozím kroku, pouze dojde k přeměně části rotační energie Země na odpovídající přírůstek kinetické energie geostacionární stanice a protizávaží.
Na konci kroku 4 tedy máme synchronně obíhající soustavu s protizávažím popuštěným o 1000 km oproti výchozímu stavu. Část energie máme uskladněnou v stále se točícím setrvačníku, a část energie jsme si půjčili od rotační energie Země. Energetická bilance je identická jako ve výchozím stavu, žádné perpetuum mobile se nekoná. Jediný rozdíl je ten, že výtah nyní vykonává horizontální kmity s úhlovou amplitudou 0,187°. Tento úhel si můžeme představit tak, že na metrové vzdálenosti nám vysekne horizontální dílek o délce 3 milimetrů.
Nedělám si samozřejmě iluze pane Nováku, že by Vám to snad nyní mělo být jasnější, ale třeba některým jiným čtenářům ano, čistě jen pro Vás osobně bych se s tím samozřejmě nepsal.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-23 05:09:52
Pan Broz, ako uvod do lacneho kabaretneho triku by to aj mohlo byt, ale kedze mam problemy s citanim, nejak mi nesedi Vasa uvaha hned v poslednom odstavci kroku 1, kde pisete nasledujuce:
"V kroku 1 je stále zachovaná bilance energie, protože jediná energetická transformace, která v tomto kroku proběhla, bylo zvýšení potenciální energie protizávaží za současného snížení jeho kinetické energie o stejnou část. Všechny ostatní energie všech ostatních komponent systému zůstaly stejné..."
Hned v dalsom odstavci ale pisete toto: "Krok 2: protože rychlost protizávaží má nyní i malou radiální složku v_p_r2=0,33 km/s, tuto energii využijeme k roztočení setrvačníku"
Kedze ste uz na zaciatku spatne zapol prvy gombik (knoflik) na koseli, nechcete si ten svoj elaborat opravit a uvazovat o tom, ze tou radialnou zlozkou ste pripravil protizavazie o cast energie, ktoru uz nedokazete vratit protizavaziu naspat? Co potom za cachre-machre budete robit, ked budete popisovat vynasanie nakladu vyssie? Ano, dalej som to uz necital...
p.s. Taktiez ste zabudol na tu fazu, ktora je zrkadlova k spomalovaniu zotrvacnika. Ta radialna rychlost zapocala z nulovej rychlosti na konecnu rychlost v_p_r2=0,33 km/s. Tuto cast energie ste schoval do ktoreho klobuka?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-23 05:29:03
he, he, krok 3.
To by som musel mat v sebe 10 piv, aby som zo seba vypustil takyto hlod: "Tento tah ale způsobí srovnání rychlostí mezi geostacionární stanicí a protizávažím"
Vedeli by nam, pan Copperfield aj nejako demonstrovat, ako to dokazete?
Uvedomujete si, ze stratou rychlosti, ku ktorej ste sa dobrovolne priznal, prichadzate o vyznamnu cast odstredivej sily za geostacionarnym orbitom a s tym suvisiacu stratu mozete kompenzovat iba silovym posobenim tangencialne, nie radialne?
Ved uz pan Hrncirik sa Vam smeje do tvare, ked popisuje nunčaku a bolaso.
Chytte si do ruky nuncaku a skuste ju roztocit. Ale bacha, aby ste dodrzal odpovedajuce podmienky ako pri vesmirnom vytahu.
Podobne ako Zemegulu a jej rotaciu povazujeme za ustaleny stav, roztocte nuncaku tak, aby ste pohybom ruky NEZRYCHLOVAL (aby ste si to nemylil so skorodovanim, tak aby ste NEAKCELEROVAL).
No dobre, argumentujete tym, ze navijakom iba pritahujete protizavazie spat. Tak teda roztocte nuncaku tak, ze pritahujete spagat/retaz na nuncake.
Ak sa Vam to podari, zaveste to na YouTube. Ako prvy na svete popriete jeden z Newtonovych zakonov.
To video je nutne, lebo ako viete, ja neviem ani citat.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-23 08:21:17
Tak som si precital Vas prispevok az do konca a to viackrat.
Moje p.s. z prveho prispevku ste vysvetlil v neskorsom texte, budis.
V kroku 4 ale stale predpokladate, ze ked Zem potiahne za lano s protizavazim, tak ze protizavazie naberie opatovne pozadovanu orbitalnu rychlost. Ak by platil Vas predpoklad, potom by ste mal ku.va problem s prekmitom protizavazia. Pouzil som podmienkovu vetu, pretoze to samozrejme nenastane, iba v hlavach fantazirujucich snilkov. Ak sa nemylim, aj toto tu zosmiesnujucou formou, a opravnene, podrobil kritike pan Hrncirik, len si netrufate mu oponovat, zrejme s argumentom, ze tiez nevie citat.
Otazka je, ak by k tomuto prekmitu doslo, ako ho ukorigujete?
Aby sa protizavazie dostalo do synchronnej uhlovej rychlosti so Zemou, musi na urcity cas dosiahnut vyssiu uhlovu rychlost, ako samotna Zem. Lenze aby nedoslo k prekmitu, musite protizavazie opat brzdit. Ale tieto otazky nerieste, lebo su len vysledkom nadseneho bluznenia nadsencov vesmirneho vytahu. Ako by povedal pan Hrncirik, v skutocnosti rieste problem, ze sa vam do retiazky na bicykli dostala nohavica a nie ze idete prave ofuknut Petra Sagana.
Opakujem, co som napisal inemu diskutujucemu panovi Matusovi vyssie o pokuse s kolesom, ktore je analogiou Zeme, s priviazanym lanom a dvoma maticami. Najlepsie, aby koleso bolo spriahnute s pomalobeznym motorom na udrzanie konstantnej rychlosti.
Zial, tento model je ale nedokonaly az tak, ze v nom neexistuje geostacionarna oblast. Spagat na modeli je v podstate cely za pomyselnym orbitom.
Realny vesmirny vytah ale pozostava z hmotnosti lana pod geostacionarnym orbitom a z hmotnosti lana a protizavazia nad geostacionarnym orbitom. Ukotvenie k Zemi by malo byt take, aby nedochadzalo k naruseniu tejto rovnovahy. Vami spominane kompenzovanie vyvola (z dovodu maleho uhla 12°) rozklad taznej sily lana tak, ze podstatna cast bude radialna a iba zanedbatelna cast bude tangencialna. Vysledkom bude potiahnutie systemu smerom dolu, vznikne nerovnovaha nad a pod geostacionarnou castou obidvoch hmotnosti cely system, bez moznosti zo Zeme situaciu riesit, pocestuje a skolabuje na zem.
Ziadna pomocka v podobe geostacionarnej stanice nepomoze, pretoze lano ju pritiahne smerom dolu tak, ze sice udrzi jej uhlovu rychlost, ale uz nie jej orbitalnu rychlost, co s poklesom orbitalnej vysky povedie ku kolapsu systemu. Pouzitie geostacionarnej stanice je vlastne len urychlovadlo kolapsu.
Kedze som prisiel az na koniec Vasho prispevku, vidim, ze na vynasanie nakladu smerom hore, a o tom je system vesmirneho vytahu, ste si uz netrufol. Asi preto, ze to obrovske mnozstvo energie nutne na vynesenie nakladu hore je mimo kompenzacne schopnosti zotrvacnika. Viete si predstavit, aku kapacitu by musel mat ten zotrvacnik, ak by mal nahradit start rakety Saturn?
Naviac to este nepocitame so stratami zotrvacnika samotneho, stratami aerodynamickeho trenia lana o atmosferu a mnoho dalsich srandiciek.
Este k Vasmu kroku 4. Ak celu sustavu posunieme o 1000 km vyssie nad geostacionarnu drahu, tak vyvstavaju tieto otazky:
- pod geostacionarnou drahou nepribudne ani kg hmotnosti lana, nad orbitom ale pribudne 1000 km lana a naviac aj geostacionarna stanica uz nebude gravitacne neutralna (ak som dobre pochopil, ze pocestuje tiez 1000 km vyssie) a protizavazie urcite pojde o 1000 km dalej. V tejto faze uz rozhodne nemozno hovorit o vybalansovanom vytahu, ale o hromade bordelu, ktore sa musi zakonite odtrhnut od zeme a odcestovat do vesmirnej tmy.
Proste, system musi byt vybalansovany, ale sila ukotvenia k zemi co najmensia, vykyv o 12° sposobi, ze protizavazie ma z pohladu rotujucej Zeme rozdielovu uhlovu rychlost, ktoru je treba kompenzovanim zastavit, dalej urychlit na vyssiu nez zemsku uhlovu rychlost a nakoniec ubrzdit na synchronizovanu rychlost. Ak hovorime o zrychleniach a spomalovaniach uhlovej rychlosti protizavazia a tym aj jeho orbitalnej rychlosti a sucasne sa ukajat predstavou, ze k tomu nebude treba sponovat silnejsie lano, je predstava smiesna. A to este stale nevynasame naklad.
Skusim pokracovat s bilanciou v kroku 5, ked je treba vyniest naklad. Predpokladam, ze k tomuto ucelu sme posunuli protizavazie o 1000 km vyssie, ze? To posunutie nam umoznilo, aby sme do protizavazia naakumulovali dostatok energie, aby sme udelili vynasanemu nakladu patricnu orbitalnu rychlost (o jej orbitalnu vysku sa stara naklad sam po ceste smerom hore). Je to tak?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-23 09:34:52
Pan Broz, mozem Vas poprosit o dokoncenie krokov energetickej bilancie tak, aby bol zavrseny cely proces vynesenia nakladu? Zatial ste skoncili pri tom, ze po povoleni lana je protizavazie o 1000 km vyssie nad geostacionarnou drahou a (ako tomu hovorim ja) energetickou pumpou sme si pripravili podmienky pre vynesenie nakladu. Principialne ten system funguje, mna vsak zaujima podstata tohoto vlakna, energeticka bilancia hlavne do momentu, ked budeme musiet vratit protizavazie na startovaciu poziciu co do vysky a rychlosti na orbitalnej drahe protizavaziu urcenej. Dakujem vopred.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-24 03:04:16
Pane Nováku, opět jste nic nepochopil, viz Vaše věta „To posunutie nam umoznilo, aby sme do protizavazia naakumulovali dostatok energie, aby sme udelili vynasanemu nakladu patricnu orbitalnu rychlost (o jej orbitalnu vysku sa stara naklad sam po ceste smerom hore). Je to tak?“
Ne, není tomu tak, to popuštění protizávaží je tam jenom proto, aby se zvětšil protitah z toho původního přebytku 3 tuny na 23 tuny, protože dole chceme na lano zavěsit dvacetitunovou kabinu, a protože nechceme, aby nám výtah spadnul na hlavu, tak chceme o dvacet tun zvýšit ten tah směrem nahoru. Bez toho zvýšení by se nám totiž z přebytku 3 tuny stal po zavěšení té kabiny deficit 17 tun a sestava by šla dolů. To zvětšení vzdálenosti protizávaží nemá nic společného s vynášením nákladu nahoru, jenom s jeho zavěšením dole – máme původně 3 tuny přebytek tahu, zvýšíme ho prodloužením lan k protizávaží na přebytek 23 tun tahu, po zavěšení dvacetitunové kabiny máme opět přebytek tahu jenom 3 tuny, prosím Vás, co je na tom tak nepochopitelného?
Náklad (ta dvacetitunová kabina) je vynášen vlastním pohonem v té kabině. Celková energie potřebná na vynesení té dvacetitunové kabiny ze zemského povrchu na geostacionární dráhu obnáší cca 300 MWh. Různé uvažované varianty pohonu kabiny výtahu jsou uvedeny přímo ve článku Vladimíra Wagnera, nebudu se proto opakovat a vybídnu Vás k přečtení toho, co jste dle Vašich vlastních slov evidentně nečetl, protože o tahání kabiny nahoru s pomocí protizávaží tam není ani slovo. Celá ta manipulace s prodloužením lana k protizávaží má pouze ten účel, aby se obnovila rovnováha sil při zavěšení kabiny dole na lano, to je celé, šplhat už musí kabina sama, navrhované metody viz článek.
Co se týče toho popouštění lana, psal jsem výše, že to popouštění bude brzděné – při nebrzdění by se nám protizávaží vzdálilo z 1200 km na 2200 km od geostacionární stanice za cca 50 minut, viz moje poznámka výše „Jinými slovy, pokud bychom lano s protizávažím nechali odvíjet na volnoběh, pak by se za těch padesát minut dostalo o požadovaných 1000 km dále. My ale chceme to lano brzdit, budeme ho tedy brzdit takovou silou, aby se do požadované vzdálenosti dostalo až za ty dvě hodiny, kdy k nám od zemského povrchu právě dorazí ta elastická tahová vlna způsobená zavěšením dvacetitunové kabiny.“ Takže nebojte se, výtah nám na hlavu nespadne, to lano se odvíjí brzděně.
Ve svých kalkulacích jsem použil zjednodušení, kdy to brzdění jsem zkrátil z těch 1000 km odvíjení jenom na posledních pár kilometrů, a udělal jsem to jenom proto, abych docílil oddělení jednotlivých etap předávání energií mezi jednotlivými komponentami systému, a aby díky tomu v každém kroku bylo evidentní, že zákon zachování energie je v každém kroku zachován – při plynulém brzdění už by ta demonstrace splnění zákonu zachování energie nebyla tak triviální, protože by docházelo k interakci více než dvou komponent současně. Ten postup se dá ale modifikovat tak, že zůstane zachováno rozfázování toho děje do časových úseků, v každém z nichž opět dochází k výměně energie pouze mezi dvěma komponentami s evidentním zachováním zákonu zachování energie, a přitom ten systém bude v režimu blízkém spojitému brzdění – stačí to vzdalování závaží rozdělit do mnoha dílčích etap, kdy v každé z nich to protizávaží vzdálíme dejme tomu jenom o metr, a každou tuto etapu rozfázujeme do těch čtyřech výše popsaných kroků. Takže místo čtyř kroků, které přeoznačíme jako A, B, C a D, budeme mít čtyři milióny kroků A_1 až D_1000000. Po každých čtyřech krocích dílčích přitom necháme systém vrátit se na tu geostacionární dráhu, odkud se nám během toho jednoho metru volného odvíjení o maličko klesne – to vrácení na geostacionární dráhu nebude žádný problém, protože protiváha má stále ten přebytek toho tahu, a systém je na zemském povrchu kotvený.
Takže výtah nám evidentně:
- ani nespadne na hlavu (je tam přebytek tahu protizávaží ty cca 3 tuny, který se navíc s odvíjením lana k protizávaží bude zvětšovat až na přebytek tahu 23 tun, který bude dosažen, až se protizávaží vzdálí o těch požadovaných 1000 km)
- ani neuletí pryč (je dole kotvený)
- ani nenarušuje zákon zachování energie (v každém z těch 4 miliónů kroků je totiž zákon zachování energie triviálně splněn, protože rozfázováním toho pohybu docílíme stavu, kdy v každém z těch čtyř miliónů kroků se vyměňuje energie vždy mezi dvěma komponentami systému)
A o to jde, ukázat, že se nejedná o žádné perpetuum mobile.
Jinak co se týče toho pokračování v těch návazných etapách, tak po skončení toho čtyřmilióntého kroku máme výtah připravený s přebytkem tahu protizávaží těch 23 tun, čiliž můžeme si dovolit zavěsit dvacetitunovou kabinu (krok čtyřmilióntý první). Tato kabina potom s využitím některé z metod popsaných v článku vyšplhá po laně nahoru. Energie potřebná na to její vyšplhání je těch už zmíněných 300 MWh, odkud se dodá je separátní problém, mimochodem dosti netriviální, protože např. na dodávání energie formou elektrického proudu by to skoro chtělo, aby to lano bylo zároveň supravodivé. To neřeším, s tím si budou muset lámat hlavu materiáloví inženýři, jestli takové lano budou umět někdy vyrobit.
Po zavěšení kabiny ten zvýšený přebytek tahu 23 tun klesne opět jen na přebytek 3 tuny. Nicméně s tím, jak kabina bude šplhat nahoru, bude klesat její tíha – jestli vzpomínáte, toto bylo místo, na kterém jste se už jednou zasekl, proto opět připomínám, že tíha tělesa je definována jako rozdíl gravitační a odstředivé síly – mimochodem ilustrativní obrázky k definici tíhy s popisem její gravitační a odstředivé složky je běžnou součástí středoškolských učebnic fyziky, nevím jaký jste ročník, jestli třeba už dnes nejsou středoškolské učebnice fyziky výrazně „měkčí“, ale za mě to bylo součástí už středoškolského učiva. Gravitační a odstředivá síla se na geostacionární dráze vyrovnají, proto tíhová síla je tam nulová. Tím pádem během toho stoupání kabiny bude ten přebytek tahu opět růst z těch 3 tun, kdy ta kabina bude zavěšená dole, až po 23 tun, kdy dorazí do geostacionární stanice.
V posledním kroku uděláme opět to, že energii uloženou v setrvačnících opět využijeme na přitažení toho protizávaží. Není to problém, protože energie setrvačníků nebyla až do této chvíle na nic čerpána (kabina lezla nahoru vlastními silami), přičemž do energie setrvačníků se uložila právě ta energie získaná bzrděním vzdalovaného protizávaží, stejná energie tedy umožní to protizávaží naopak zase přitáhnout do výchozí polohy. Tak jako došlo u oddalování protizávaží k zaostávání protizávaží za geostacionární stanicí – finálně toto bylo řešeno na úkor rotační energie Země – tak nyní dojde k opačnému jevu: při přitahování protizávaží toto předstihne geostacionární stanici, čímž se finálně ta rotační energie Země zase maličko zvýší. Rotační energie Země tedy finálně nijak neutrpí, pouze se dočasně neznatelně sníží, aby se později zase zvýšila.
Mimochodem, ty první čtyři milióny kroků ještě před zavěšením kabiny to protizávaží rozkmitají, ale to jsem už dříve opakovaně zmiňoval. V té idealizaci, kdy jsou ty čtyři milióny kroků zjednodušeny do čtyřech kroků jsem sice skončil u stavu, kdy geostacionární stanice i protizávaží jsou zpožděny za ukotvením, díky čemuž nastane výměna energie mezi výtahem a rotační energií Země, kdy rotační energie Země se o maličko zmenší s tím, že ze synchronizuje pohyb toho výtahu. Bude tam překmit, kdy v opačné fázi se zase naopak rotace Země maličko zrychlí, čímž zbrzdí překmitnutý výtah – to jsou ty horizontální kmity, které už jsem dříve zmiňoval. Dá se ale ukázat, že ty kmity budou velmi pomalé, geostacionární stanice bude kmitat kolem své průměrné úhlové pozice s úhlovou amplitudou 0,187° a s periodou cca 106 hodin, tedy více než čtyři dny. Během tak dlouhé doby už se dá dávno realizovat další vynášecí cyklus, který vhodně načasován ty předchozí kmity zase vyruší, takže nemá smysl nějak prožívat ten překmit, při plném provozu a inteligentní synchronizaci k němu totiž vůbec nemusí dojít. I kdyby se ale vynášelo jenom jednou za dejme tomu měsíc, tak by se prostě ta sestava kývala s amplitudou pouhých 0,187° s periodou cca čtyři a půl dne, nic katastrofického by se nedělo.
Zbylo ještě něco, co je Vám nejasného?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Vladimír Wagner,2017-08-24 11:30:16
Díky moc Pavlovi Brožovi za excelentní rozbor. Myslím, že už by mělo být vše principiální jasné. Mám jen jednu drobnou opravu překlepu v jeho textu. Ta energie potřebná pro vyšplhání kabiny s hmotností 20 kg není 300 MWh, ale 300 kWh. Pokud se to podělí 20, tak je to těch často zmiňovaných zhruba 15 kWh/kg potřebných na vynesení 1 kg. Ono je možná někdy nejnázornější obrázek. Proto asi poprosím redakci, aby mi přidala k článku malou poznámku, kde by byl jednoduchý graf, jak se mění potenciální a kinetická energie kabiny o hmotnosti 20 kg při vynášení a kolik energie (dodávané pohonem kabiny, předpokládá se elektrický) je potřeba na vynesení do daného místa výtahu.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Vladimír Wagner,2017-08-24 11:38:38
Tak omluva Pavlovi, má to správně s 20 tunovou kabinou :-)) Já jsem uvažoval malinkou, jen nákladní pro 20 kg :-) Přechod z kg na tuny je přechod z kWh na MWh. V každém případě bych chtěl dát ten obrázek, protože to krásně názorně ukazuje, jak se ta energie musí pohonem dodávat.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-24 14:14:02
To je v pořádku, já děkuji za velice pěkný článek. Vím, že toto téma spolu s dalšími několika (např. budoucnost mezihvězdných letů, solární plachetnice, ale i jiné) tvoří konstantu mezi Vámi oblíbenými tématy, a že se k nim opakovaně vracíte, rád si vždycky přečtu další update, protože se z pokaždé dozvím, co se od minule v dané problematice podařilo vymyslet nového.
Samozřejmě dnes nikdo nemůže s určitostí vědět, jestli pozemský kosmický výtah někdy bude nebo nebude zkonstruovatelný, nicméně každá podobná vize obnáší ohromné množství problémů, které se ale postupně dají řešit. Možná se nedají vyřešit všechny, možná nakonec zbyde nějaký problém, který se ukáže jako principiálně nepřekonatelný, a který tím pádem celou vizi pohřbí. Nicméně tam ještě nejsme, zatím žádný takový principiálně nepřekonatelný problém nikdo v této vizi neobjevil, dílčí problémy je stále možné řešit. A právě proto si vždycky rád přečtu vždy po pár letech Váš další update té problematiky, protože se člověk dozví vždy nějaké nové podněty a přístupy k řešení těch kterých klíčových problémů.
To, co je na celé věci úsměvné, je že se vždycky dopředu vždy vyrojí dostatek proroků tvrdících, že to nikdy nebude fungovat nebo dokonce že to skončí katastrofou. Je zajímavé, že tito proroci se rekrutují prakticky výhradně z lidí, kteří sice nemají potřebné vzdělání na to, aby vynášeli příslušné závěry, ale to jim nevadí, oni prostě ví, že to nebude fungovat, a místo čísel a výpočtů budou argumentovat vágními metaforami. Osobně nepochybuji, že třeba bratři Wrightové a všichni podobní vynálezci spoustu takových lidí kolem sebe také v hojném množství potkávali.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Vojta Ondříček,2017-08-24 15:23:28
Souhlasím s vámi, pane Broži, že diskuze je nutná a seriózní diskuze že je přínosná.
Ale upozornil bych na mylnost přirovnávání dobové skepse k létajícím strojům těžším vzduchu ke skepsi k realizaci vesmírného výtahu. Ptáci a hmyz jsou a byli těžší vzduchu a létali. Ta skepse se zakládala spíš na představě stroje s mávajícími křídly poháněné lidskou silou letce, tedy stroje kopírujícího hmyz, ptactvo a netopýry (abych byl úplný).
Na druhou stranu však nemáme žádný přírodní příklad vesmírného výtahu.
Dosud se diskuze zabývala hlavně možností realizace výtahu, ale to je podmíněno realizací materiálu pro lano o užitné měrné pevnosti aspoň 100GPa. Trochu mi to připomíná jednu povídku od Wodehause, myslím, že se jmenuje Slepičí farma. Zkrátka problémy je nutno řešit od základu a dokud nemám dořešen základ (materiál lana) je další diskuze jen platonická.
Nezanedbatelný, ale obcházený problém, je problém bezpečnosti vesmírného výtahu. Hmotnost lana od bodu GEO k povrchu bode kolem 400tun, při známé délce. To švihnutí Země kolem rovníku si sotva někdo vezme na svědomí. Ta kabina pro dopravu lidské posádky by musela být též vybavena záchranným zařízením skládajícím se jak z reaktivních pohonů, tak ablativního štítu a systému padáků (obdobně jako je má Sojuz, ovšem reaktivní pohon o výkonu potřebném na snížení kabiny z GEO na vstup do atmosféry rozumnou rychlostí).
Jinak vám i panu Wágnerovi děkuji za informativní a inspirující diskuzi, fakt.:-)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-24 18:50:29
Pane Ondříček, ten argument s tím možným švihnutím lana kolem Země při jeho přetržení je jenom další nedomyšlený strašák. Ta část lana, která se bude nacházet nad 30 km nad povrchem, při svém pádu bezpečně shoří v atmosféře. Těch zbývajících 30 km švihne do oceánu, v němž bude zaparkovaná v dostatečné vzdálenosti od pevniny ta plovoucí základna toho výtahu. Stačí kolem této základny dodržovat cca třicetikilometrový bezpečnostní rádius, a jediné, co tím lanem přepůlíte, bude maximálně nějaký žralok, který bude ve špatnou chvíli na špatném místě. Ten třicetikilometrový konec lana se pak samozřejmě zase navine na tu plovoucí základnu.
Totéž platí co se týče utržené kabiny. S dopravou osob se samozřejmě začne teprve až tehdy, až bude celý ten systém spolehlivě odzkoušený několika lety provozu neživého nákladu. Samozřejmě i poté se může stát nehoda, která bude stát životy pasažérů - je to smutné, ale nehody se prostě stávají, koukněte se jenom kolik v průměru zahyne ročně lidí v letecké dopravě. Je snad kvůli tomu zakázáno létání? Samozřejmě že ne, každá nehoda je podrobně vyšetřována a závěry z ní slouží pro další zvyšování bezpečnostních standardů. Přesto přese všechno se těm smrtelným nehodám nelze vyvarovat, to je prostě daň za využívání civilizačních výdobytků, jako je letecká doprava. Alternativou je ji nepoužívat, pokud vím, tak cestování letadlem ještě nikde na světě žádný zákon nepřikazuje. Nejinak tomu bude i s cestováním kosmickým výtahem. A nepochybujte o tom, že na bezpečnost přepravy osob kosmickým výtahem bude kladen násobně vyšší důraz než na bezpečnost cestování letadly, prostě už jenom z toho důvodu, jak drahá sranda ten výtah bude, takže nikdo nebude chtít co chvíli řešit náklady na jeho znovuzprovoznění, o poškozené pověsti coby použitelného dopravního prostředku ani nemluvě.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-24 19:25:28
Dobry vecer, pan Broz a dakujem za dalsi Vas prispevok do diskusie. Zatial co ini krochkaju blahom nad Vasim prispevkom slepo veriac, ze to mate v poriadku, mne tam zostali niektore veci nejasne.
V predoslom prispevku ste napisal toto:
"Krok 2: protože rychlost protizávaží má nyní i malou radiální složku v_p_r2=0,33 km/s"
Ako to dobre chapem, tak tou rychlostou je takmer rychlost zvuku, alebo sa mylim?
V dalsom prispevku ste napisal toto:
"stačí to vzdalování závaží rozdělit do mnoha dílčích etap, kdy v každé z nich to protizávaží vzdálíme dejme tomu jenom o metr, a každou tuto etapu rozfázujeme do těch čtyřech výše popsaných kroků"
Dalej nebudem citovat, ze Vam ide o prebytok tahu 3 tony.
Mam tomu rozumiet tak, ze chcete ten prebytok tahu 3 tony rozbehnut na vzdialenosti 1 meter na rychlost 330 m/s a este to aj ubrzdit aj na nulu?
Dakujem vopred za odpoved.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-24 23:55:40
Dobrý večer, ne, těch 330 m/s (aneb cca rychlost zvuku ve vzduchu za normálního tlaku a teploty jak správně píšete) byla sumární hodnota platná při tom přílišném zjednodušení, kdy by se to udělalo to vzdálení o 1000 km s navijákem na volnoběh pouze v jednom kroku. Při rozdělení na postupné vzdalování vždy o jeden metr to pro ten jeden metr samozřejmě vyjde výrazně méně. Nebude to ale lineární závislost, ale zhruba odmocninová, protože ta odchylka je odchylkou tečny od kružnice (protizávaží se do uvolnění pohybovalo po kružnici, po uvolnění po její tečně), a tato odchylka nevzrůstá lineárně. Ta odmocninová závislost na délce kroku mimochodem koresponduje s lineární závislostí v energii na délce kroku, finálně tedy při tom rozdělení dostaneme zhruba stejnou energii jako bez toho rozdělení (kinetická energie závisí kvadraticky na rychlosti).
Při vzdálení o 1 m proto ta radiální složka rychlosti bude 0,338 m/s, zatímco při vzdálení o 1000 km (tedy miliónkrát větším) byla 0,33 km/s (tedy jen tisíckrát větší, viz ta odmocninová závislost). Takže necháme ten přebytek tahu 3 tuny rozběhnout o jeden metr dále (o jeden metr v radiálním směru), dostaneme tak radiální složku rychlosti 0,338 m/s, a tu ubrzdíme na nulu. Celý postup opakujeme miliónkrát, ve výsledku budeme mít protizávaží vzdálené o požadovaných 1000 km dále, tzn. místo o 1200 km bude vzdáleno od geostacionární stanice o 2200 km.
Zdůrazňuji ale, že to přerušované brzdění v praxi nemá smysl, v praxi se bude brzdit plynule, je to zde použito jenom pro snadnější náhled, že systém v každém kroku ctí zákon zachování energie. Což ale mimochodem plyne už z teoretického popisu, protože jde o systém konzervativní, ve kterém nepočítáme s disipativními prvky (při brzdění totiž předpokládáme ukládání příslušné energie do setrvačníku, nikoliv přeměnu kinetické energie na teplo).
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-24 23:25:29
Ak sa nemylim, cela operacia ma trvat cca 50 minut, co je cca 3 000 sekund.
Takze to zrychlenie a ubrzdenie prebytok tahu 3 tony (az 23 ton) na jednom metri sa ma uskutocnit za 0,003 sekundy?
Aky reakcny cas ma(l) Usain Bolt?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-25 00:37:56
Ne, tam nebude lineární čas, při tom rozdělení na milión etap bude sumární čas výrazně delší, platí zde totéž jako pro tu rychlost, která taky nezávisí lineárně na délce toho kroku - na rozdíl od energie.
Znova ale zdůrazňuji, že v praxi se bude brzdit spojitě. Při spojitém brzdění (tj. spojitém převodu kinetické energie vzdalujícího se protizávaží do energie setrvačníku) se celá operace dá stihnout za necelé tři hodiny. To spočteme jednoduše - máme hmotnost protizávaží m=750 tun, máme radiální sílu (přebytek tahu) 30 kN, dejme tomu že brzdění pomocí setrvačníků budeme provádět tak, aby se setrvačníky roztáčely silou rovnou polovině toho tahu, tedy 15 kN. Výsledný tah působící způsobující vzdalování protizávaží bude tedy jen F=15 kN. Tento tah bude udělovat protizávaží radiální zrychlení a=F/m=15000/750000=0,02 ms^-2. Dráhu s=1000 km = 1000000 m toto protizávaží urazí za čas t=odm(2s/a)=odm(2000000/0,02)=10000 s=2 h 47 min.
Celý proces akumulace energie do setrvačníků se dá samozřejmě zpřevodovat tak, aby dojezd byl plynulý, ne jako u starých výtahů, které se zastavovaly trhnutím.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-25 14:16:38
Takze mame v kabaretnom klobuku dvoch kralikov, jeden o case cca 50 minut, aby ste k nemu pridal druhy o case 2 hod. 47 minut.
Ak si dobre pamatam, tak mame za ulohu presunut protizavazie o 1000 km a vypocital ste nam, ze radialna zlozka rychlosti je 0,338 m/s.
Ak vzdialenost 1000 km podelim spominanou rychlostou, pribudne mi do klobuka treti kralik s casom 2,9 miliona sekund, resp. 821 hodin. To uz je penkne macatej kralik, ze? Nezda sa to na chybu sposobenu zaokruhlovanim, ze?
Problem je, ze dvaja z tych troch kralikov su falosni a vy, pan Broz, ako varietny umelec, nenatahujte divakom zvedavost, prezradte nam, ktory je ten pravy?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-25 16:05:08
Pane Novák, těch 50 minut bylo uvedené jako doba, za kterou se protizávaží stihne vzdálit v radiálním směru o 1000 km, pokud by vůbec nebylo brzděné. Sám jsem tam zdůrazňoval, ve skutečnosti bude brzděné, dobu jsem odhadnul na dvě hodiny, a to se dá volbou zpřevodování setrvačníku a tedy i volbou poměru mezi silou vytahující protizávaží a silou roztáčející setrvačníky docílit. Pokud se speciálně volí poměr těch sil jako jedna k jedné, tedy pokud zvolíme převodový poměr tak, že 15 kN je síla vzdalující to závaží a 15 kN síla roztáčející setrvačníky, tak ta doba vyjde na 10000 s, což jsou ty 2 hodiny a 47 minut. Pokud byste zvolili ten poměr jinak, vyjde jiná doba. Tak např. pokud byste zvolil ten poměr tak, že setrvačníky by byly roztáčeny během celé doby pouze silou 1,064 kN místo 15 kN, dostali byste přesně ty dvě hodiny. To by ale nebylo výhodné, protože pak by bylo nutné úplně na konci zastavit to lano prudkým trhnutím (neboli rychlým absorbováním cílové radiální rychlosti do energie setrvačníků), což není optimální.
To rozfázování toho pohybu do těch čtyř miliónů kroků, kdy se nejprve nechá lano rozvíjet jenom a metr a pak se úplně zastaví, bylo použito jenom kvůli té ilustraci, že zákon zachování energie je pak snadno nahlédnutelně splněn, protože v každém z těch dílčích kroků se energie vyměňuje jenom mezi dvěma komponentami. Toto opakované zastavování protizávaží je ale krajně nevýhodné z toho důvodu, že jeho rychlost po každém metru klesne na nulu a musí se proto znova obtížně rozpohybovávat. To je přesně ten důvod, proč to pak vede k enormnímu nárůstu toho potřebného času - ne, nejsou to zaokrouhlovací chyby, ten čas opravdu takto naroste v důsledku toho opakovaného zastavování toho protizávaží, které ale bylo použito jenom pro tu demonstraci splnění zákona zachování energie. Jak už jsem zmínil, pro člověka disponujícího příslušným teoretickým vzděláním není nutné ilustrovat splnění zákona zachování energie na základě takovéhoto umělého rozfázování pohybu, protože stačí si uvědomit, že v hamiltoniánu popisovaného modelu se nenachází žádný disipativní člen, proto je zákon zachování energie pro tento systém automaticky splněn.
Ve skutečnosti bude to odvinování lana brzděné, přičemž ale nebude opakovaně zastavované - tzn. radiální rychlost závaží se bude při konstantním poměru mezi urychlovací silou a silou roztáčející setrvačníky bude stále zvětšovat. Ta rychlost nebude klesat opakovaně na nulu a protizávaží se tedy nebude muset opakovaně obtížně rozpohybovávat. Proto ta doba jeho vzdálení při vhodné režimu brzdění může být docílena na ty dvě hodiny místo těch 821 hodin, které vzniknou jako důsledek opakovaného zastavování toho protizávaží.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-25 20:17:21
Nemate tam stale, nahodou, chybu? Tvrdite, ze prevodovy pomer nech je 1:1, takze pre vzdalovanie protizavazia mate 15 kN.
Podla toho, co pisete, je tento tah 15 KN konstatny po celu dobu 10 000 sekund.
Kedze na hmotny pohybujuci sa predmet posobi nemenna sila 15 kN, mozeme s istotou tvrdit, ze protizavazie akceleruje. Celu tu dobu.
Hmmm, ale vy tvrdite, ze po 10 000 sekundach sa protizavazie zastavi.
Ked vydelim vzdialenost 1 000 km casom 10 000 sekund, vyjde mi nutna priemerna rychlost 100 m/s.
Ak by som riesil presun protizavazia ja, tak pri najjednoduchsom modeli prvu polovicu drahy venujem akceleracii a druhu deceleracii.
Pre zachovanie priemernej rychlosti 100 m/s by som v strede trasy musel dosiahnut rychlost 200 m/s. To je, sic asi nepatrne, viac, nez Vami spominanych 0,338 m/s.
Zatial co v prvej polovicke som mohol prebytok tahu 15 kN ukladat do zasobnika, v druhej polovicke budem potrebovat 45 kN na zastavenie radialnej zlozky rychlosti protizavazia. Bilancne to vidite v poriadku?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-25 22:54:10
Ne, obě dvě ty čísla náleží jinému režimu povolování lana, těch 10000 sekund vyjde pro spojité brzdění lana se zůstatkovým přebytkem tahu 15 kN (kdy zbylých 15 kN je spotřebováváno na roztáčení setrvačníku). Kdežto ta rychlost 0,338 m/s vyšla při přerušovaném zabrzďování lana po každém metru odvinutí. Oba dva jsou to jiné režimy, prakticky použitelný je jenom ten se spojitým brzděním, protože to miliónkrát opakované zastavení až na nulovou rychlost samozřejmě vede k neúměrně velkému nárůstu požadované doby.
Ten rapidní nárůst té doby je ale naprosto v pořádku, vznikne vždy když rovnoměrně zrychlený pohyb rozdělíme do mnoha etap. Urychlujeme-li těleso na dráze délky s pomocí konstantního zrychlení a, urazí tuto dráhu za čas t=odm(2s/a) a bude mít na konci té dráhy rychlost v=odm(2a*s) a urychlováním získá energii E=(1/2)m*v^2=m*a*s. Pokud budeme těleso během jeho urychlování zastavovat vždy po milióntině dráhy, urazí každý úsek s1=s/1000000 za čas t1=odm(2s/1000000a)=(1/1000)t, tedy těch milión dílčích úseků se zastavováním urazí za čas t2=1000t. Na konci každého úseku přitom bude mít rychlost v1=odm(2a*s/1000000)=(1/1000)v, a energii E1=m*a*s/1000000=(1/1000000). Opět, protože je těch úseků milión, získá to těleso miliónkrát za sebou energii rovnou milióntině původní energie, tedy pokud tu energii někde odevzdává (např. ji na konci každého úseku trhnutí lana předá geostacionární stanici), tak celkově tak odevzdá stejnou energii, jako kdybychom ten původní úsek nedělili.
To je ta mnou výše zmíněná odmocninová závislost rychlosti a lineární závislost energie na zkrácení délky té dráhy. Když dráhu zkrátíme miliónkrát, rychlost se nezmenší miliónkrát, ale jen tisickrát, tedy jako odmocnina toho zkrácení. Oproti tomu energie se zmenší opravdu miliónkrát, díky čemuž dostaneme ve výsledku stejnou energetickou bilanci, protože miliónkrát menší energii odevzdá miliónkrát za sebou.
Ano, pro plynulý dojezd bude na konci působit na lano větší síla, než odpovídá tomu původnímu přebytku tahu 30 kN. Ono ale na to lano nepůsobí síla jen toho přebytku, lano bude ve skutečnosti napínáno silou ekvivalentní 753 tun, tedy 7530 kN, a koneckonců i to provozní kolísání napětí musí umožnit dodatečné zavěšení dvacetitunové kabiny, tedy zvýšení síly napínající lano na 7730 kN, proto ten dojezd nebude představovat problém. Samozřejmě lze volbou poměru mezi urychlovací a zpomalovací etapou docílit libovolně malého přepětí nad těch původních 30 kN, cenou za to by ale samozřejmě bylo výrazné prodloužení času potřebného pro to odvíjení. Těch 45 kN co uvádíte ale není nijak nebezpečná hodnota, a ta doba odvíjení by se pro ni neprodloužila zase až tak tragicky.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-25 23:14:59
Jo, ještě jsem si dodatečně všiml Vaší poznámky, že tvrdím, že se po 10000 sekundám závaží zastaví. Ne, to jsem nikde netvrdil, pouze jsem zmínil, že výrazně jiný poměr (zhruba 1:29 místo 1:1) mezi těmi silami by nebyl výhodný, protože by se na konci muselo to lano zastavit prudkým trhnutím. Při tom poměru 1:1 se samozřejmě na konci bude muset taky zastavit trhnutím, ale ne tak velkým. Pro plynulý dojezd je ale samozřejmě nutné ke konci to odvíjení lana naopak zpomalovat, tedy přejít od kladného poměru zbytkové urychlovací síly a síly roztáčející setrvačník k poměru zápornému. Tedy např. zpřevodovat ten moment na tom setrvačníku z těch 15 kN na těch 45 kN jak píšete.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-25 23:38:01
Pan Broz, ja viem, ze ste nikde VYSLOVNE netvrdil, ze po 10 000 sekundach sa protizavazie zastavi. Ale predsa predmetna diskusia je o tom, ze po presune zavazia o 1 000 km toto zostane na novom orbite. Ak ma zostat na novom orbite, ako to dosiahne, ked nie tym, za sa na novom orbite zastavi? Pozate tu o chytrej horakyni?
Vsimli ste si, ze tych krochkajucich blahom v diskusii ubudlo?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-25 23:38:54
errata ... poznate
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-26 01:05:26
Pane Novák, protože už mě to nebaví, tak jenom zrekapituluji Vaše komické vstupy, a tím skončím, pak si pište do libosti co budete chtít, opravdu mě to nezajímá:
Takže na začátku hypotetizujete o nutnosti mít na protizávaží raketové motory, jednoduše z toho důvodu, že jste nedokázal pochopit prostou funkci těch navijáků, pomocí kterých se dá regulovat velikost toho tahu protizávaží i bez raketových motorů. Současně s tím nabízíte autorovi služby Vaší společnosti, která může předložit Vaše vlastní řešení (bez pochopení toho původního).
Pak argumentujete údajným „významným energetickým počinem“ už při povolení toho navijáku o pouhý milimetr, což jsem vyvrátil výpočtem, že odmotání lana o jeden milimetr ve skutečnosti zvětšuje přebytek tahu o pouhých 20 miligramů (tedy 200 mN), což samozřejmě není vůbec žádný „významný energetický počin“.
Pak po sérii dalších Vašich mnoha a mnoha nepochopení se konečně stává nepřehlédnutelně zřejmým, že jste naprostý fyzikální neználek poté, co jste mi připsal tvrzení že „na geostacionární dráze je gravitační síla nulová“, které jsem nikdy neřekl, psal jsem o tíhové síle, která je rozdílem síly gravitační a síly odstředivé, takže tíhová síla je na rozdíl od gravitační na geostacionární dráze opravdu nulová, na což Vás správně upozornil pan Wagner. Na což jste reagoval otázkou co je zdrojem síly nad geostacionární drahou, což bylo opravdu velice zábavné, dalo by se říct že to byl zlatý hřeb celého Vašeho vystoupení :-))) V tomto okamžiku už bylo naprosto zřejmé, že se nebavíme pouze s člověkem, který pouze nepochopil spoustu dříve zmíněných a zřejmých věcí, ale že se bavíme s člověkem, který ač nemá potřebné fyzikální znalosti, dokonce ani některé potřebné ze středoškolské fyziky, tak mu nechybí hypertrofovaná sebedůvěra v to, že může do diskuze o této problematice něčím podnětným přispět.
V tomto duchu se pak odvíjela ta diskuze dále, pokračoval jsem v ní jenom proto, že jste tam naplácal spoustu evidentních nesmyslů a bylo mi líto ponechat ty ze čtenářů, kteří se ve fyzice dostatečně neorientují, napospas Vašim bludům.
Rozdíl mezi námi dvěma je v tom, že já mám státnice z teoretické fyziky, a Vy máte pouze tu nekritickou sebedůvěru, že bez znalostí fyziky všem vytřete zrak a ukážete, že je všechno úplně jinak. To je opravdu velice komické, připomíná mi to jednu postavičku ze známé knížky Ondřeje Sekory, a tím nemyslím postavičku Ferdy Mravence.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Miroslav Novak,2017-08-26 08:19:49
Pan Broz, ja nemam problem uznat:
1. ze som toho v tejto diskusii naplacal dost za nezmyslov,
2. ze si Vas vazim ako odbornika v teoretickej fyzike,
3. ze trpezlivo vysvetlujete svoje stanoviska k diskutovanej teme,
4. a ze ziadny clovek nie je neomylny.
- Vy ale stale svoju neomylnost uznat nechcete,
- a ked ste zatlaceny do kuta,
- tak sa uchylite ku klasickemu klise,
- opat zacnete urazat diskutujuceho,
- svoju neschopnost zakryjete listom mojich neschopnosti (pocet nezmyslov vytvorenych neteoretickym fyzikom v porovnani k Vasim, ale je alarmujuci prave na Vasej strane),
- a akoze urazene opustite diskusiu.
Pritom ten Vas konstrukt stroskotal uz len na tom, ze nedokazete obhajit uz ani len posun protizavazia, kde mate rozkmit od 0,338 m/s az po 300 m/s. Chaos v case potrebnom na presun ste uz ani nezacal obhajovat. Vykonat tah 45 kN priznate takym sposobom, akoby som na to zabudol ja...
Moje uvodne tvrdenie je, ze balancovanie protizavazia iba protitahom je nemozne.
Vase tvrdenie, ze zo zeme dokazete balancovat protizavazie bez potreby dodatocnej energie.
Uz len pri manevri presunu protizavazia ste sam priznal tuto potrebu. Potrebu tak velku, aka je velkost samotneho prispevku zeme do projektu. Ze vlastne zo zeme musite kompenzovat ten prispevok zeme? Na co nam vlastne je ten prispevok zeme?
A co potom, ked budeme vynasat naklad?
Co sa tyka Brouka Pytlika, je dobre, ze ten pocit nemate o sebe ako o jedinom neomylnom cloveku pod slnkom.
Dakujem za diskusiu a vo Vasom zivote Vam prajem vela uspesnych projektov a najma zdravie.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Bilancia
Pavel Brož,2017-08-26 22:37:42
Pane Nováku, opravdu nemám problém uznat svou chybu, samozřejmě je dělám také. Těžko po mě ale můžete chtít, abych uznal chybu tam, kde špatně přečtete a promícháte moje tvrzení, ze kterých pak vykonstruujete věty typu: "Pritom ten Vas konstrukt stroskotal uz len na tom, ze nedokazete obhajit uz ani len posun protizavazia, kde mate rozkmit od 0,338 m/s az po 300 m/s. Chaos v case potrebnom na presun ste uz ani nezacal obhajovat." Pokud si nedáte práci aspoň přečíst to co napsal ten druhý a snažíte se protiargumentovat na základě svých vlastních smyšlenek, tak se nedivte, když Vám to ten druhý s chutí vrátí jakmile bude mít příležitost poukázat na Vaši nekompetentnost vynášet závěry v oboru, ve kterém se on orientuje mnohem lépe než Vy. Což potom Vy vyhodnocujete jako urážení diskutujícího. Nejste první a určitě ne ani poslední diskutér, kdo se zde na oslu cítil být uražen tím, když jsem poukázal na jeho zásadní neznalosti.
Takže co se týče těch Vašich tvrzení, že nedokážu obhájit ani posun protizávaží, tak obhájil jsem ho výše dokonce na třech různých režimech. A taktéž jsem obhájil ten "chaos v čase potřebném na přesun". Všechno je to výše, stačí to pouze znova přečíst, tentokrát pořádně, proto je zbytečné to všechno opakovat. Jenom zesumíruju odlišnosti těch režimů vzdalování protizávaží - výše jsem popisoval tyto režimy:
a) volné popuštění protizávaží až do konečné vzdálenosti o 1000 km dále, v cíli ho trhnutím zastavit;
b) opakované volné popouštění o jeden metr, po každém metru malým trhnutím zastavit, tedy celkem jeden milión popuštění s jedním miliónem trhnutí;
c) spojité brzdění lana bez jeho zastavování.
Každý z těch režimů má své výhody a nevýhody. První z nich je výpočetně velice jednoduchý, protože dochází k předávání energií postupně vždy jen mezi dvěma komponentami systému, není problém tedy problém u něj prokázat splnění zákona zachování energie. V praxi je ale tento režim použitelný jenom pro velmi těžkou geostacionární stanici, kdy by její hmotnost výrazně převyšovala hmotnost lana pod sebou, teprve pak by bylo její klesání tíhou spodního lana tak malé, že by se dalo dorovnat dodatečně.
Druhý režim odbourává potřebu mít stanici výrazně těžší než lano pod sebou, protože je vždy dovytahována po každém metru vzdálení protizávaží. I v tomto režimu dochází v každé z těch miliónů etap k předávání energií postupně vždy jen mezi dvěma komponentami systému, takže i zde je snadné prokázat splnění zákona zachování energie. Klíčová nevýhoda tohoto režimu ale plyne z toho opakovaného zastavování závaží na nulovou radiální rychlost, která v každé z miliónu etap naroste jen na 0,338 m/s místo 330 m/s jako v prvním režimu. Díky tomu tisíckrát naroste čas potřebný na to vzdálení, což jsem ilustroval na tom příkladu s nepřerušovaným a přerušovaným rovnoměrně zrychleným pohybem.
Třetí režim odbourává obě nevýhody předchozích dvou režimů - není nutné mít výrazně těžší stanici než lano pod ní, při spojitém brzdění totiž je tato stanice stále tažena přebytkem tahu nahoru (dole je přes spodní lano ukotvená k Zemi), takže neklesá, není ji tedy nutno dodatečně dovytahovávat. Také tam nedojde k nárůstu toho času na tisícinásobek, protože v tomto režimu nedochází k miliónkrát opakovanému zastavování lana na nulovou rychlost - lano bude mít nulovou rychlost až v cíli. Čas potřebný pro vzdálení toho protizávaží o 1000 km se dá korigovat postupným měněním převodového momentu roztáčejícího setrvačník.
Bohužel třetí režim zase ztrácí výhody dvou předchozích režimů, u kterých se dalo elementárními kroky prokázat splnění zákona zachování energie. To neznamená, že by se snad v tomto režimu energie nezachovávala, pouze to není jednoduché prokázat pouze s využitím středoškolské fyziky. S využitím vysokoškolské fyziky už samozřejmě není problém nahlédnout, že i v tomto režimu se energie zachovává, prostě se např. stačí kouknout na tvar hamiltoniánu celého systému a je vidět, že se energie zachovávat bude. S použitím jenom středoškolské fyziky je to ale problém ukázat.
Takže tohle už je opravdu poslední moje reakce na Vaše komentáře v tomto článku. Také Vám přeji hodně úspěchů a samozřejmě hlavně zdraví.
Výtah na LEO
Jenda Hrach,2017-08-21 07:00:51
Chtěl bych se zeptat, co si myslíte o následujícím designu výtahu na LEO: http://diyhpl.us/~bryan/papers2/space/Low%20cost%20design%20of%20an%20orbital%20ring%20-%202017.pdf (mirror: https://jenda.hrach.eu/f2/Low%20cost%20design%20of%20an%20orbital%20ring%20-%202017-1.pdf).
Ve zkratce jde o to, že na nízkou oběžnou dráhu (~300 km) vypustíme desetitisíce elektricky nabitých vodivých objektů, kterým udělíme rychlost vyšší, než je potřeba pro jejich cílovou výšku - budou se tak postupně vzdalovat od Země - a následně tam nainstalujeme platformu, která bude mít rychlost geosynchronní (tj. nestabilní zase tím způsobem, že bude mít tendenci padat k Zemi). Tato platforma bude elektricky nabité šrouby pomocí magnetu „tahat k zemi“ a tím se bude sama připozvedávat. Lano pak může být dlouhé jenom 300 km, což už by mělo být realizovatelné se současnými materiály.
Přijde mi to jako fascinující znásilnění nebeské mechaniky a bohužel se svojí středoškolskou fyzikou nedokážu posoudit pokročilejší problémy, které mohou hrozit.
A pak se chci ještě zeptat, jak již bylo v diskuzi naznačeno, zda existuje nějaká horní mez pevnosti materiálu, který je vůbec možné [pomocí chemických vazeb] vyrobit (například by člověk tipl, že z uhlíku nelze vyrobit nic pevnějšího než ten ideální řetěz C=C=C=C), a zda by takový ideální materiál vůbec dostačoval k výrobě geostacionárního výtahu.
Re: Výtah na LEO
Pavel Brož,2017-08-21 13:20:41
Bylo by to nestabilní, extrémně drahé, a navíc by to stejně velmi rychle přestalo fungovat v důsledku vybíjení toho náboje, o což by se postaraly částice slunečního větru - nabité desky by totiž náboje stejného znaménka odpuzovaly, zatímco náboje opačného znaménka přitahovaly, proto by tam potřebně velký náboj dlouho nevydržel.
Horní mez pevnosti materiálu skutečně existuje, řádově nic silnějšího než vazby C=C neexistuje. Volbou materiálu lze možná realizovat vazby o dejme tomu dvacet procent silnější, ale více těžko.
Zázračné materiály
Vojta Ondříček,2017-08-20 13:56:40
Ano, takové potřebujeme.
Potřebujeme akumulátory do automobilů s energetickou hustotou 1kWh / 1kg, potřebujeme supravodiče pro teploty do 100°C, potřebujeme materiál na fůzní reaktor odolávající teplotám milionů K ... a na realizaci výtahu na orbit materiál o minimálně (b)stonásobné(b) pevnosti nejlepší oceli, pokum možno s hustotou do 1000kg / m^3. Pochopitelně materiál elektricky nevodivý, nemagnetický, odolný proti všemu s nekonečnou životností.
Dokud takový materiál, ze kterého by se dalo spléct lano o délce 2 x 36 tisíc km, nenajdeme, tak o realizaci levné dopravy na orbit výtahem můžem jen snít.
Odkaz k tématice :
http://www.wikiwand.com/de/Weltraumlift
No a jen na okraj - použil jsem primitivní algoritmus jednoho tabulkového kalkulátoru na výpočet váhy nosného lana z dostupné oceli (pevnost 1,5 GPa., tedy žádná rezerva) na zátěž závažím o hmotnosti 1000kg při délce pouhých 500km. Nebudu napínat - Lano ukotvené v této výšce se zavěšenou zátěží o mase 1000kg by mělo hmotnost 102Gt, tedy 102Pg. S ocelí to prostě nejde.
Když ovšem pevnost materiálu zvýším na desetinásobek pevnosti oceli (při stejné hustotě), tak by takové lanko mělo hmotnost pouhých 14t.
Na dvojnásobnou délku, tedy výšku ukotvení v 1000km nad povrchem planety, mi vyjde hmotnost lanka na 203t.
Já vím, na první pohled neuvěřitelné ... a budu rád, když to některý z vážených kolegů přepočítá. Jinak mi napadá ta pohádka o skromném vynálezci hry šach, který si jako odměnu nežádal víc než pár zrnek rýže, za první políčko jedno zrnko, za druhé dvě zrnka a za každé další políčko vždy jen dvojnásobek počtu předešlého políčka.
jenom ještě zmínka
Pavel Brož,2017-08-20 00:41:03
Jak tady zaznělo to strašení s tím ohřátím o mnoho tisíc stupňů a uvařením výtahu. Takže vezměme onen odhad 14,8 kWh/kg jakožto energetický nárok dopravy a délku lana 35800 km od povrchu Země ke geostacionární dráze. Předpokládejme, že výtah pojede rychlostí až 1000 km/h, což je podle mě velmi velká rychlost, při nižší rychlosti to ale vyjde co se týče chlazení ještě příznivěji. Takže při rychlosti 1000 km/h potrvá cesta nákladu 35,8 hodin, tzn. že když na tuto dobu rozložíme oněch 14,8 kWh/kg, dostaneme že potřebujeme uchladit příkon 14,8/35,8 = 0,413 kW/kg, tedy 413 W/kg. Pokud bychom na každý kilogram hmotnosti včetně hmotnosti výtahu věnovali 1 metr čtvereční chladiče, tak podle Stefanova-Boltzmannova zákona by to odpovídalo rovnovážné teplotě cca 19 stupňů Celsia, viz https://cs.wikipedia.org/wiki/Stefan%C5%AFv-Boltzmann%C5%AFv_z%C3%A1kon .
Jinými slovy, pokud by se jako topení použilo pouze teplo generované pohonem, a pokud by na jeden kilogram hmotnosti připadnul jeden metr čtvereční chladiče, pak by průměrná teplota uvnitř byla devatenáct stupňů Celsia místo oněch údajných mnoha tisíc stupňů. A to se bavíme pouze o pasivním chlazení vyzařováním, samozřejmě že s aktivním chlazením by to bylo mnohem efektivnější. Aktivní chlazení by mohlo fungovat podobně jako lednička, kde jedna část by se ochlazovala, zatímco druhá, pasivně chlazená oteplovala, čímž by se zvyšoval účinek toho pasivního chlazení.
Pokud bychom uvažovali hmotnost kabiny dejme tomu jedna tuna, pak požadovaná plocha chladiče by byla tisíc metrů čtverečních, tedy cca čtverec o straně 31 metrů, anebo disk o poloměru 17,8 metru, což není nic nerealizovatelného.
Suma sumárum, nic katastrofického v důsledku těch dopravních energetických nároků nehrozí.
Re: jenom ještě zmínka
Pavel Brož,2017-08-20 00:56:21
Těch tisíc metrů čtverečních samozřejmě může mít i výhodnější podobu než čtverec nebo disk - např. kulová plocha o poloměru 9 m s otvory nahoře a dole, kterými by procházelo lano, anebo podobu šestice dvojic na sebe kolmých panelů, každá z dvojic trčících ve směrech os +-x, +-y, +-z, atd. atd..
parametry
Libor Tomáš,2017-08-19 21:48:21
Mohl by nekdo uvest zhruba jak tluste by muselo byt takove grafenove lano a kolik by to vazilo? Jestli by nebylo jednodussi dosypad na mount everest dalsich 10 km, dovnitr integrovat delo a strilet. Lidi by tim posilat nesli, ale na dodavku toaletniho papiru na iss by to mohlo stacit.
děkuji za velice pěkný článek
Pavel Brož,2017-08-19 18:45:02
Jinak co se týče všech těch odsudků typu nejde, nebude možno, vyloučeno, katastrofa atd., tak sám mám na tuto problematiku optimistický pohled. Na rovinu říkám, že si myslím, že nikdo z nás, co tady dnes k tomuto článku diskutujeme, se kosmického výtahu ze Země na geostacionární dráhu nedožije. Věřím ale, že ti nejmladší z čtenářů se možná za cca padesát let až šedesát let dočkají menší měsíční verze.
Proč si to myslím? Protože to bude finálně ekonomicky výhodnější. Věřím, že Měsíc bude do třiceti let využíván k těžbě surovin, svého času se diskutovalo např. o heliu 3, viz https://en.wikipedia.org/wiki/Helium-3#Extraction_from_extraterrestrial_sources . V jedné variantě kosmického výtahu by lano tvořilo uzavřený pás, kde váha vynášeného nákladu by byla kompenzována vahou jiného snášeného nákladu, teoreticky tedy s nulovými energetickými nároky. Náklad vynášený z povrchu Měsíce na jeho oběžnou dráhu lze sice vynést alternativními prostředky vzhledem k tamnímu vakuu, např. railgunem. Ale railgun nepomůže při snášení těžebních strojů z oběžné dráhy Měsíce na jeho povrch. Samozřejmě že ze začátku těžby budou tyto kalkulace podružné, protože úplně na začátku bude muset být gigantická investice do vytvoření těžební infrastruktury, která se vrátí až za hodně let. S postupem času se ale začnou udržovací výdaje snižovat, a časem se nakonec ukáže, že se vyplatí zainvestovat i do toho měsíčního výtahu. Těžební společnost, která takový výtah zprovozní jako první, získá nemalou výhodu nad ostatními konkurenty.
Myslím si pouze, že mezi měsíčním a pozemským kosmickým výtahem bude tolik rozdílů, že vlastně půjde o zcela rozdílné projekty, které toho kromě jádra té myšlenky bude technicky spojovat jen zanedbatelně malá část použitých technologií. Rád bych ale věřil tomu, že dejme tomu za třicet let po zprovoznění měsíčního výtahu se podaří realizovat i výtah pozemský. Očekávám ale, že mezi konstrukční obtížností obou bude ale možná podobný rozdíl, jako mezi konstrukční obtížností jaderné a termojaderné (tj. fúzní) elektrárny. Hodně věcí bude prostě někde úplně jinde, potřebná pevnost materiálů, přítomnost atmosféry, samozřejmě v článku zmíněné kosmické smetí (zatím naštěstí absentujícího na oběžné dráze Měsíce), atd. atd..
Osobně jsem ale přesvědčen, že kosmický výtah ze Země na geostacionární dráhu je dnes sice jen extrémně smělý sen, ale že bude dříve nebo později realizován. Od Ciolkovského rovnice uběhlo 54 let do letu první družice Země. V jeho době byl Konstantin Eduardovič Ciolkovskij považován za nenapravitelného fantastu a snílka, zatímco dnes drtivá většina lidí bere vynášení družic na oběžnou dráhu za tak banální věc, že by kvůli tomu rozhořčeně protestovala, kdyby byl přenosem startu nahrazen jejich oblíbený plytký večerní seriál. Tak, jako nepochybuji o tom, že se podaří vyřešit všechny problémy stojící dnes v cestě řízené termojaderné fúzi, tak stejně tak nepochybuji o tom, že dříve či později se podaří vyřešit i problémy spojené s pozemským kosmickým výtahem. Tím nemyslím banální problémy typu odvod tepla, což mi přijde, jako v počátcích letectví strašit tím, že létat nebude nikdy možné kvůli hrozbě bouřek a blesků. Odvod tepla a podobné podružnosti JE už dnes řešitelný problém.
Samozřejmě jiná otázka je timeline. Z historie vývoje řízené fúze víme, že je snadné původní odhady překročit i o mnoho desetiletí, a nejinak tomu může být i u vývoje pozemského kosmického výtahu. Bude pozemský kosmický výtah realizován ještě do konce tohoto století? Netuším. Věřím že jednou realizován bude, nevěřím pouze, že kdokoliv z nás se toho dožije. Oproti tomu ale opravdu věřím tomu, že nejmladší z dnešních čtenářů se dožijí té měsíční verze.
Akcie dolu Bezruč budou velmi slibné
Josef Hrncirik,2017-08-19 20:50:19
Při stejných hmotnostech fárajících a vytěžovaných havířů v cyklu korečkového pásu nevznikají žádné energetické nároky při jejich opakované recyklaci.
Na rozdíl od Země, která se otáčí;
na Měsíci, který na mě stále vystrkuje stejnou tvář, nebudou problémy s realitou zdánlivého Coriolisova zrychlení ani při různých hmotových tocích výtahu z dolu a dolů.
Jak však na Luně získat geostacionaritu a vytěžit i její rotační energii?
Re: Akcie dolu Bezruč budou velmi slibné
Pavel Brož,2017-08-19 22:56:59
Místo geostacionární dráhy by se využil librační bod L1, ten by měl být ve vzdálenosti cca 61500 km od středu Měsíce, tedy necelých 60000 km od jeho povrchu. Tedy vzdálenost větší než od povrchu Země ke geostacionární dráze, přesto to ale vychází výrazně schůdněji než v případě pozemského kosmického výtahu. Mezi L1 a Zemí by bylo umístěno to protizávaží vyvažující těch 60 tisíc km lana od L1 k povrchu Měsíce.
Co se týče toho dvojitého pásu, tak ten by se uvažoval mezi povrchem toho tělesa (Země nebo Měsíce podle toho jestli uvažujeme pozemský či měsíční kosmický výtah) a mezi tím gravitačním centrem toho výtahu, tj. geostacionární drahou v případě Země či bodem L1 v případě Měsíce. Nebylo by to tak, že prakticky nulové (samozřejmě nikdy ne úplně nulové) dopravní náklady by byly když snášený i vynášený náklad by byly stejně hmotné - ne, ten snášený náklad by musel být výrazně hmotnější než ten vynášený nahoru, protože tíha tělesa nahoře je mnohem menší než toho dole. Takže pokud by se použilo přirovnání k Cimrmanovu výtahu, bylo by dokonalé v tom smyslu, že horníků fárajících dolů by muselo být více (dokonce výrazně více) než těch fárajících nahoru. V praxi by to bylo např. tak, že dolů by se snášely stroje a různá zařízení, nahoru by se vynášela podstatně menší hmotnost těženého koncentrátu např. obsahující to kýžené He3. Z rozdílných hmotností nákladu samozřejmě plyne, že od určité vzdálenosti by to lano muselo být permanentně bržděné (určitě by se dalo ale využít nějaké formy rekuperace energie, např. roztáčením setrvačníků při brždění).
Re: Re: Akcie dolu Bezruč budou velmi slibné
Juraj Chovan,2017-08-20 01:23:41
Za tento príspevok som Vám veľmi vďačný, je to prvý krát čo ohľadne témy vesmírneho výťahu čítam o verzii "pásového dopravníka". Všetky články na túto tému ku ktorým som sa doteraz dostal pojednávali výhradne o jednosmernom výťahu hoci ten je podľa mňa konštrukčne zložitejší ako dvojitý pás. Pri dvojitom páse máme problém navyše, lebo nechceme aby sa nám pás "zamotal", to je však pomerne jednoducho riešiteľné inštalovaním korekčných trysiek na kabínach upevnených na páse. Naproti tomu jednosmerný výťah vyžaduje komplikovanú konštrukciu samohybnej kabíny, jej napájanie energiou, odvod tepla atď. V neposlednom rade, takáto hi-tech kabína je iba jednorazovo použiteľná čo výrazne navyšuje náklady na prevádzku.
Súhlasím že mesačný výťah (alebo mesačný pásový prepravník) budeme mať zrejme skôr ako pozemský. Ak však získame dostatočne pevný materiál na konštrukciu pozemského výťahu, bude zaujímavé nahradiť ním pás mesačného prepravníka a predĺžiť ho z L1 až po vrchné vrstvy atmosféry Zeme (nároky na pevnosť pásu sú len minimálne väčšie oproti klasickému výťahu, samozrejme pás musí byť oveľa dlhší; premenlivá vzdialenosť Zeme a Mesiaca by sa riešila navíjaním a odvíjaním pásu). Stanica vysiaca na konci pásu sa voči zemskému povrchu pohybuje rýchlosťou porovnateľnou s rýchlosťou dopravného lietadla. Stanica došlý náklad z Mesiaca (celú kabínu) navijakom spustí po lane do výšky cca 10km nad zemský povrch, odtiaľ bude kabína s nákladom zhodená na padáku. Zároveň bude iná kabína s nákladom prevzatá z nákladného lietadla a navinutím lana vytiahnutá na stanicu odkiaľ vesmírnym pásom poputuje na Mesiac. (Operácia s odovzdaním naloženej kabíny z letiaceho lietadla na staničné lano sa javí ako extrémna, ale uvedomme si že US Army v pohode dokáže za letu tankovať lietadlá takže neriešiteľný problém to asi nebude.)
Bonus na záver: V súvislosti s ťažbou nerastných surovín na Mesiaci sa dá predpokladať že viac materiálu bude treba dopraviť z Mesiaca na Zem ako naopak. Keďže (kvôli vyššej gravitácii) povrh Zeme má nižšiu potenciálnu energiu ako povrch Mesiaca, úhrnná eregetická bilancia mesačno-zemského prepravníka je pozitívna. Množstvo zdrojov minieme pri budovaní tejto infraštruktúry, avšak samotnú prepravu nákladov medzi Mesiacom a Zemou budeme mať "zadarmo".
Re: Re: Akcie dolu Bezruč budou velmi slibné
Josef Hrncirik,2017-08-20 07:28:27
Deus in machina.
Hlavnímu inženýrovi OKLD a Nebeskému Mechanikovi 1**.
Houstone, mám problém
Josef Hrncirik,2017-08-20 21:26:48
Zdravím z Tuhé věže ruského kosmického výtahu z rovníkového kosmodromu dočasně zakotveného uprostřed rostoucí Venezuely.
Zakoupil jsem si vytažení hlavního závaží na geostacionární dráhu, nad něj vytáhl i protizávaží s Veverkami (tažní šplhavci), vše do patřičné výše a při dobrém dolarovém kurzu.
Vše jsem řádně spojil vyhovujícím lankem ze supravodivého kovového argonu a sledoval nebývalou stabilitu těsně nad zemí visícího konce lanka, které ani nebylo nutno zajistit stanovým kolíkem.
Po připnutí kabinky s Veverkou se těžiště Nesmírného i jeho těžišťová rychlost snížily pod potřebné geostacionární a Nesmírný přestal geostacionárně strmět.
Tahem Veverek se situace poněkud zlepšuje, těžiště Nesmírného se stoupáním kabinky pomalu vrací k geostacionární orbitě.
Rychlost těžiště je však stále malá.
Vlivem Coriolisovy síly kabinka stoupající po lanku se odchyluje mírně na západ, kam unáší i konec lanka, který jsem raději přivázal ke kolíku a tím též trochu zapřáhl do chomoutu i matičku Gaiu.
Nepříznivým úhlem rozkladu sil se brzy lanko velmi napjalo a začalo příšerně kvílet, ale po ráně kladivem do kolíku zmlklo.
Určitě nestihlo vyzářit více než 1 kT (TNT) akustické energie, kterou jsem tedy pro jistotu ihned odepsal z bilance energie Nesmírného.
Abych kompenzoval snížení těžiště připnutím kabinky, zapnul jsem zdvih kompenzačního závaží výše nad geostacionární orbitu.
K mému zděšení se Veverky buď odrazily od závaží a zmizely v prázdnotě Všehomíra, ale změna těžiště i hybnosti závaží byla zanedbatelná, nebo se jim podařilo nějak se zachytit Nesmírného a po návratu do výchozí polohy na Nesmírném byla změna hybnosti a polohy těžiště přesně nulová.
Pomůže narovnání lanka a jeho začarování zmagnetováním na supertuhý nosník po kterém pak Veverka závaží vytáhne do požadované výše?
Pro zvýšení rychlosti těžiště na požadovanou geostacionární rychlost musím skutečně vystřelit vypočtenou rychlostí a směrem alespoň Veverčí inkrement?
Není lepší se nenápadně vzdálit po hlavním schodišti?
Re: Houstone, mám problém
Josef Hrncirik,2017-08-20 21:55:27
Tahem Veverek (Vnitřní Síly) se těžiště Soustavy ani Její Hybnost ani nehne.
Bylo to jen klasické rušení GPC v okolí ruských vojenských základen.
Re: Houstone, mám problém
Pavel Brož,2017-08-20 23:01:16
Takhle, on to bezesporu bude dynamický systém, ve kterém stav, kdy lano po celé jeho délce od jeho konce na zemském povrchu až po ukotvené protizávaží nad geostacionární drahou bude v přímce, bude nutno chápat jenom jako jakési nulté přiblížení. Geometrie té sestavy se bude bezesporu v průběhu manipulací s nákladem měnit, a tyto změny bude nutné kompenzovat.
Úplně na začátku ale předpokládejme, že konec lana na zemském povrchu bude kotvený, a že celá sestava nebude v úplně přesné rovnováze, ale že tam bude maličký přebytek toho tahu směrem nahoru, kompenzovaný tím kotvením.
V první řadě se předpokládá s tím, že jak lano od geostacionární dráhy směrem k zemi, tak lano od geostacionární dráhy směrem k protizávaží, bude na té centrální stanici navinuto na navijácích, které bude možné popouštět nebo přitáhnout. Pokud se popustí lano směrem k protizávaží, to se začne odvíjet, díky tomu se zvětší rameno od té geostacionární dráhy k protizávaží. Zdůrazňuji, že nyní bude záležet na detailech, jejichž ignorováním je možné dojít k naprosto odlišným důsledkům. Momentálně tímto detailem bude, že popouštění toho lana bude probíhat tak pomalu, že stále bude přetrvávat ten tah směrem nahoru působený tím protizávažím (jinými slovy, že ten naviják nepustíme úplně na volno)
Pomalé odvíjení lana směrem k protizávaží přinese hned několik důsledků. Jednak se tím posune těžiště celého výtahu, které už nebude na geostacionární dráze, ale nově nad ní. Opět zdůrazňuji, že třeba zrovna tady záleží na tom detailu, kdy to lano popouštíme pomalu, takže se stihne vyrovnávat ta síla až k té pozemské kotvě. Dále ale také dojde ke snížení rychlosti toho nového těžiště, takže toto už nebude viset nad stejným zemským poledníkem, ale začne se přesouvat mírně na západ (sama stanice na geostacionární dráze přitom nadále bude na geostacionární dráze, pouze už těžiště výtahu nebude v ní, poloha těžiště výtahu se totiž změní jenom díky zvětšení ramena k tomu protizávaží). Kromě toho ale i to protizávaží se po tom popuštění bude po nějakou dobu pohybovat směrem na západ, a to ještě rychleji než nové těžiště. Díky tomu se geometrie celého systému dočasně změní z úsečky na lomenou úsečku.
Protože systém je kotvený, tak nás poloha jeho těžiště vzhledem ke geostacionární dráze zajímá jenom proto, abychom si udělali představu o zvětšování či zmenšování té odstředivé „napínací“ síly. My to těžiště můžeme samozřejmě zase snížit tím, že na pozemský konec toho lana pověsíme nějaké užitečné závaží, při vhodném vyvážení tak docílíme toho, že nejnovější těžiště systému bude opět na úrovni geostacionární dráhy, nebo lépe malilinko nad ním, pokud si chceme uchovat maličký nadbytek toho tahu nahoru. Tento nadbytek totiž budeme potřebovat k tomu, aby se nám tou odstředivou silou z té lomené úsečky stala opět nelomená úsečka, podobně jako když nad hlavou rotujeme míčkem na provázku, přičemž na tom míčku je dalším provázkem navázaný další míček – zvýšením rotace dojde přechodně k zalomení mezi těmi dvěma provázky, které se ale nakonec opět vyrovná.
Protože ale ve vesmíru je vakuum, tak tam se nám ta zalomená úsečka nevrátí definitivně do původní nelomené úsečky, ale překmitne. Jinými slovy, to protizávaží bude v důsledku těch manipulací „horizontálně“ oscilovat kolem nějaké polohy dané momentální délkou toho ramena k protizávaží (přičemž tato délka bude určena momentálním užitečným zatížením výtahu, protože chceme, aby v průměru bylo jeho těžiště na geostacionární dráze, resp. jenom malilinko nad ním).
Tato oscilace protizávaží se bude muset využívat při načasování těch zdvihů. Samozřejmě není cílem tyto oscilace neomezeně zvětšovat, právě naopak, což povede k tomu, že pouze v některé hodiny bude vhodné výtah zatížit. Jinými slovy, může se vám stát, že doběhnete ke spodní stanici toho výtahu a budete se chtít okamžitě rozjet nahoru, protože budete mít přesně za 35,8 hodiny nahoře důležitou schůzku. Obsluha výtahu vám ale znuděným hlasem řekne, že budete muset půl dne počkat, než protizávaží překmitne do optimální polohy, kdy teprve bude vhodné na to lano přivěsit tu kabinu s vámi. Ač se to mnohým cestujícím nebude líbit, instrukce obsluhy bude vhodné respektovat, aby se zamezilo destabilizaci celého systému, který by se v důsledku toho mohl nebohým rovníkovanům zřítit na jejich hlavy.
Mimochodem, všechny tyto komplikace s horizontální oscilací protizávaží v důsledku popouštění lana si můžeme odpustit u měsíční verze výtahu, kde místo nesolidní geostacionární dráhy figuruje solidní librační bod L1, který se stále nachází na témže místě na spojnici mezi Měsícem a Zemí (zatímco těleso orbitující na geostacionární dráze se vůči spojnici Země – Měsíc pohybuje). Díky tomu je u měsíčního výtahu manipulace s protizávažím o hodně jednodušší – popuštěním protizávaží se zvýší těžiště výtahu, to se dá zase vhodně snížit zavěšením užitečného nákladu, žádné komplikace s horizontálními oscilacemi. Měsíční výtah je prostě v mnoha ohledech jednodušší.
Re: Re: Houstone, mám problém
Josef Hrncirik,2017-08-21 06:58:52
Díky.
Kolík se při dešti vytrhl ze Země a tak už raději ručkuji dolů po zábradlí u hlavního schodiště.
Už se těším NATO, že pod geostacionární orbitou zbytek sjedu serpentinami po zábradlí pohodlně posazen na zakázané asbestové (serpentinitové) hasící dece.
Re: Re: Re: Houstone, mám problém
Milan Krnic,2017-08-21 18:46:22
Už se na ty úsečky těším. Na papíře je to hračka. :)
Hurvínkův myšlenkový pokus (model vesmírného výtahu)
Josef Hrncirik,2017-08-22 07:42:28
1.Na rovníku zakotvi do Země volně otočný kloub či osu v ložiskách směřující směrem sever-jih.
2.Pořiď si mašli přesně délky geostacionární výšky nad povrchem Země na rovníku .
3.Mašli ukotvi jedním koncem do kloubu či osy.
4.Volný konec Mašle natáhni po rovníku směrem na Západ.
5.K Mašli přivaž kouli dělovou (raigunovou), tzv. Protizávaží.
6.Mašli řádně naimpregnuj UV zářením se vytvrzující pryskyřicí.
7.Kouli naláduj do gunu zaměřeného vertikálně a o polednách vystřel do ozonové díry směrem vzhůru, aby nad kloubem měla uvázaná obíhající koule mírně nadgeostacionární rychlost.
8.Aby koule po čase nedopadla na velké město na nulté rovnoběžce náhodou ležící o délku Mašle východně,
s mírným předstihem než nyní již Nanejvýš Tuhá Mašle bude vertikální, nech po ní vyšplhat od kloubu k protizávaží užitečnou zátěž takové hmotnosti, aby soustava nyní byla přesně geostacionární.
9.Snadno a lehce takto vyneseš náklad na geostacionární orbitu a omezíš kmity.
10.Nestarej se o to, co s nákladem a Protizávažím, zachránil jsi Velké Město před neodvratnou zkázou dopadem Protizávaží, pokud bys nekonal či vyslal malou Zátěž.
Je pravdivé proroctví, že pokus o vynešení příliš hmotného nákladu skončí zničením velkého města na Západě?
Josef Hrncirik,2017-08-22 10:27:01
Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Josef Hrncirik,2017-08-22 22:12:39
snad názorností usnadní výpočty energií, momentů hybnosti či sil i u navijáků a pochopitelně to umožní místo šplhavců či tlačivců a brzdičů (tj. Veverek) bez problémů návnadu ochutit navijáky.
Nosník snadno udělám stejně dlouhý jako lana (jenom jsem je naimpregnoval a vytvrdil).
Tím potlačím komplikace s kmity či rozklady sil a možná půjde pohodlně bilancovat snad skoro vše a nebude nás zdržovat znuděný hlas obsluhy: vyčkejte prosím správné fáze kmitu.
Ohledně rychlosti zvuku v grafenu, uklidňuji vystrašené ovce, že je určitě min. 10 km/s u předpjatého i 20 km/s.
I čekání na vlnu z přetržení bude kratší.
Je to jasné. Grafen je mnohem tužší (modul pružnosti v tahu než u oceli) a mnohem lehčí než ocel (hustota).
Bude to dobré do pancířů, pokud ihned nezvětší ráži a rychlost.
Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Miroslav Novak,2017-08-22 23:23:42
Uz je to asi aj roky, co citavam Vase prispevky a nikdy, okrem satiry, nemozem najst moment, kedy by Vase vyjadrenia boli mimo misu.
Aj pod tymto clankom su Vase prispevky k veci.
Sarkazmus vo Vasich prispevkoch je vlastne psychologicka obrana voci prispevkom, ktore prekracuju hranice elementarnej logiky. A je jedno, ci medzi nich patri aj autor clanku.
Drzim Vam palce v boji so samozvanou elitou.
Re: Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Vladimír Wagner,2017-08-23 05:15:53
Pane Nováku, vidím, že máme velmi odlišný pohled na smysl diskuze pod články i samotných článků. Já si myslím, že jsou k tomu, aby jsme si vzájemně věci osvětlili a rozšířili své znalosti, Vy to chápete jako boj s někým.
Re: Re: Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Milan Krnic,2017-08-23 06:44:11
Zde se ovšem, jak jste pane Wagnere zmínil již dříve, vede polemika, a ta bojem je.
Holt "daň" za komplikované nemateriální téma. Normál.
Re: Re: Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Miroslav Novak,2017-08-23 08:24:30
Pan Wagner, cim to bude, ze takto ste nepocastoval aj pana Broza, ktory ma tu uraza, ze neviem citat? Mate dvojaky meter?
Re: Re: Re: Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Josef Hrncirik,2017-08-23 09:56:17
Polovina viny je na autorovi, větší zbytek na čtenáři,
že neumí pracovat s ?hamiltoniánem dvojitého kyvadla se 2 nezávislými navijáky při nezbytném ukotvení v Zemi (tj. ?rotující neinerciální soustavě) pochopitelně v nekastrofálním režimu chodu v zásadě nutně převážně nadgeostacionárním.
(Já jsem naletěl reklamě, že je to neškodný geostacionární projekt).
Kupodivu systém (prý) lze při respektování všech kmitů pomalu (s malou produktivitou vytahování), vrátit do původních stavů s vyjímkou nepatrného zpomalení rotace Země (což ale šetří energii pro vytahování na laně. Bilance energií je zajímavá hlavně pokud ji rekuperují navijáky ?bez rekuperace i 10x horší.
Banky však zajímá intenzita využívání zařízení, skoro mrtvý (nesdílený) kapitál nezafinancují.
Dokáže terorista zničit výtahem město na východě či západě, nebo jen vypustit výtah na svobodu?
Dá se výtah rozkmitat, že do použitelného stavu přijde na malou dobu až v příští pětiletce?
Není zcela triviální popsat, co se vlastně děje,
když Baron Prášil vystupuje na stoličku v systému bez gravitace, s gravitací
ev. v kombinacemi s rotací,
vytáhne se tam kladkostrojem či vesmírným výtahem či tahem za vlasy.
Celému lidstvu to trvalo dost dlouho a stále to někteří zkouší nepřipraveni na zkoušku.
Re: Re: Re: Re: Re: Úvahy o chování vytvrzeného lana jako tuhého nosníku a vystřelení systému vhodnou rychlostí
Josef Hrncirik,2017-08-23 12:18:58
Neustále obdivuji pracovitost a pečlivost, trpělivost i znalosti pánů Wagnera i Brože, které se exponenciálně umocňují v jejich tandemu.
Nicméně jsem si vzpomněl na zoufalou výčitku Dr.Vašuta studentům:"Já Vás to učím furt dokola už 40 let a vy se to pořád nejste schopni naučit!"
Vladimír Wagner,2017-08-19 10:31:44
Diskuzi na Oslovi považuji za velmi užitečnou a důležitou. Snažím se psát o věcech, které mě hodně zajímají, a dost o nich vím. Přesto jsem však u širších témat nucen zabrousit i do oblastí, kde si úplně v kramflecích jistý nejsem. Takže se přirozeně dopustím i řady chyb, nepřesností a neobratností. Zároveň popisovaná tématika často zasahuje do oblastí, kde je odpověď na otázky otevřená a dosud neznámá. Navíc se k tomu přidají překlepy a upsání. Také se pochopitelně nelze na omezeném prostoru článku zmínit o všech problémech a tématech, které se popisované oblasti dotýkají. A právě diskuze nám pak může hodně pomoci, aby se společným úsilím věci vysvětlily, ozřejmily a dozvěděli jsme se něco nového a zajímavého. Prosil bych, aby každý z nás zvážil, zda příspěvek, který do diskuze dává, k takové plodné polemice vede.
Pan Jaroslav Pešek napsal „Vesmírný výtah je sice pěkný sen, ale neproveditelný. To už se spíš dřív začne používat antigravitace, než se vyrobí vesmírný výtah.“. Vyjádřil tím, že on osobně si myslí, že se vesmírný výtah nikdy nemůže realizovat. Je to jeho názor a kterýkoliv z čtenářů může vyjádřit svůj. Ovšem jeho výrok nepřinesl k tématu vesmírného výtahu nic nového a smysluplného. Kdyby každý čtenář udělal, to co on, tak sice dostaneme statistiku názorů čtenářů Osla v hlasování „vesmírný výtah se možná realizuje“ nebo „vesmírný výtah nikdy nebude“, ale nic nového a zajímavého se nedovíme a nevím, jaký by taková diskuze pod článkem měla smysl.
Pan Hrnčiřík téměř ke každému příspěvku v diskuzi na Oslovi přidá svůj textík. Docela často upozorní na nepřesnost či problém, ale to se ztrácí ve formulaci, která alespoň mě připadá do značné míry jako exhibice, a často proložená i nesmysly. Jeho podněty, které by mohly pomoci při osvětlování zajímavého problému či vyjasnit nepřesnost, tak zanikají a jeho textíky podnětnou diskuzi ubíjí místo, aby ji iniciovaly.
Omlouvám se zmíněným pánům, že jsem jejich příspěvky zde použil jako příkladů, ale přesto jsem si dovolil je využít k vyjádření svého osobního názoru na smysl diskuzí pod články. Možná se mýlím, ale posouzení je pochopitelně na každém z diskutujících.
Re:
Milan Krnic,2017-08-19 11:51:04
https://cs.wikipedia.org/wiki/Polemika
"Polemika (z řec. polemiké techné, válečnické umění) znamená původně umění sporu, později odborný, politický nebo umělecký spor vůbec. Na rozdíl od diskuse a dialogu, které hledají spíše shodu, cílem polemiky je vyvrátit názor protivníka, případně ho i odborně nebo lidsky zpochybnit"
Vesmírný výtah je ve stádiu úvah, a o úvaze věcně diskutovat nelze.
Otázkou je, co je podle našich představ oblast vesmírného výtahu se dotýkající, o které by šlo diskutovat. Když je to tak vzdálené, abstraktní téma.
( :) ) majitelé pozemků se případného rizika vyvlastnění pro účely kotvení výtahu bát nemusí.
Re: Re:
Vladimír Wagner,2017-08-19 19:58:17
Pane Krniči o řadě témat, které se dotýkají vesmírného výtahu, lze polemizovat i diskutovat, stejně jako o slunečních plachetnicích, fúzní elektrárně či termojaderném pohonu kosmických lodí. I zde už jsou oblasti, kde se pracuje na potřebných technologiích a materiálech a i v článku jsou popsány experimenty ve vesmíru se systémy s různě dlouhým lanem a s materiály s různými vlastnostmi, které se zlepšují potřebným směrem. Zlepšuje se maglev i railguny. Je možné diskutovat možnosti ochrany konstrukcí a testovat je v reálu na ISS. Ono ostatně, když se podíváte do té mnou doporučené literatury, tak vidíte, že fúra odborníků o tom nejen velice plodně diskutuje a polemizuje, ale dokonce navrhují a realizují experimenty v potřebném směru. Ano, realizace vesmírného výtahu je velmi daleko. A souhlasím s Pavlem Brožem, že se toho nikdo z nás nedožije, i přes zlepšující se zdravotnictví :-) Také si však myslím, že moji synové by se měsíčního výtahu dožít mohli. Jsem si však jistý, že i já se ještě dožiji velice zajímavých technologických úspěchů v řadě oblastí, které s vesmírným výtahem souvisí. Ať už zajímavých aplikací lan na orbitálních drahách, aplikacích grafenu, rychlého maglevu či extrémně vysokých budov.
Re:
Kája Dolejší,2017-08-19 12:46:13
A proto na Osla už několik let (až na několik drobných výjimek, kterých poté lituji) příspěvky do diskuse nepíši. Mám pak totiž neodbytný pocit, že diskutuji s porouchanými chatovacími boty s umělou inteligencí. Vlastně sem chodím číst stále měně často a méně rád. A to jsem s Oslem od jeho úplného zrodu.
Teď
Mojmir Kosco,2017-08-19 08:10:49
příjde naivní mýšlenka .Proč to musí být výtah ,proč to nemůže být skutečně pouze lano nespojené pevně ze zemí ale opětovně natahováno a spouštěno? Rovněž asi je energicky nejnáročněnjších prvních 50 km a po dosažení potřebné rychlosti asi již není potřeba již vest loď po laně .
Re: Teď
Vladimír Wagner,2017-08-19 10:37:53
To lano je tam dost důležité. Řekl bych, že moc pěkně to osvětluje Honza Bílek v odkazovaném příspěvku: http://www.osel.cz/4999-vesmirny-vytah-pokus-o-odpovedi-na-otazky.html (první část). Vůbec všechny odkazované texty Jana Bílka doporučuji zájemcům o tématiku k přečtení.
Re: Re: Teď
Miroslav Novak,2017-08-22 10:11:31
No, musim povedat, ze uz v roku 2010 boli ludia, ktori spochybnovali energeticku bilanciu a pan Bilek sa s argumentami vysporiadal naprosto chlapsky. Mlcanim.
Ved je to jednoduche.
Lano je ukotvene o zemegulu a spolu s protizavazim je vynesene na orbitalnu drahu.
Lano delime na dve polovice.
Prva polovica lana je pod geostacionarnym orbitom, teda je tahana zemegulou.
Druha polovica je nad geostacionarnym orbitom a je spolu tahana odstredivou silu vlastnou hmotnostou a protizavazim.
Co je zdrojom sily protizavazia a lana nad geostacionarnym orbitom?
Anketa:
a) je to rotujuca zemegula?
b) je to nejake deux ex machina mimo sustavu (Mesiac, Slnko, Mliecna draha)?
c) je to hybnost udelena lanu a protizavaziu pri instalacii vesmirneho vytahu?
Ak vasa odpoved nie je c), potom skuste odpovedat na dalsiu otazku,
Ak pri vyneseni nakladu na orbitalnu drahu bolo protizavazie nutene kompenzovat rozdiel v rychlostiach nakladu z polovicky na 4 km/s, co je zdrojom energie, ktora nasledne musi byt vratena protizavaziu?
a) je to rotujuca zemegula?
b) je to nejake deux ex machina mimo sustavu (Mesiac, Slnko, Mliecna draha)?
c) lano a protizavazie nedokaze samo od seba kompenzovat straty, iba ak s pomocnym zdrojom (raketa, FVE, Jadrovy pohon, proste cokolvek).
Ak vasa odpoved nebola c, ste clovek, ktory veri nekonecne rotujucim magnetickym motorom, chemtrails a pod.
Re: Re: Re: Teď
Vladimír Wagner,2017-08-22 11:29:40
Problém je, že ani v jedné anketě jste nezařadil správnou odpověď. V první otázce je odpověď, že působící síla v daném místě systému je dána rozdílem gravitační a odstředivé síly a musí jej vyrovnávat síla vytvářená závěsem. U těch procesů, které popisuje Pavel Brož pak jde o vzájemné přeměny potenciální a kinetické energie. Přičemž se využívá i procesů rekuperace dodané energie (přeměna různých forem kinetické energie). Nejde pochopitelně o žádné perpetum mobile. Pro vynášení se musí energie dodávat (v úplně optimálním případě těch zmíněných 15 kWh/kg). A také se musí nahrazovat ztráty při provozu navijáků , ovšem ty mohou být velmi malé (o tom všem Pavel Brož velmi podrobně píše).
Re: Re: Re: Re: Teď
Miroslav Novak,2017-08-22 12:41:08
Pan Wagner, pozeram vo Vasom prispevku smajlika ako dokaz, ze ten prispevok mienite ako zabavny.
Ja sa pytam: "Co je zdrojom sily protizavazia a lana nad geostacionarnym orbitom?"
A Vasa odpoved je: "V první otázce je odpověď, že působící síla v daném místě systému je dána rozdílem gravitační a odstředivé síly a musí jej vyrovnávat síla vytvářená závěsem"
Na otazku na energiu odpovedate silou, na otazku, co je zdrojom sily pre protizavazie, odpoviete, ze to je sila vytvarana zavesom.
Pricom zdrojom sily protizavazia nie je sila, ale hybnost tohoto protizavazia. Trosku rozdiel, ze?
Dalej dalsia perla hodna urazky Newtonovych zakonov: "U těch procesů, které popisuje Pavel Brož pak jde o vzájemné přeměny potenciální a kinetické energie".
Uz ste aj zrejme pozabudli z uciva fyziky, ze zdrojom energie nemoze byt vzajomna konverzia Vami spominanych energii. Tym zdrojom musi byt nieco mimo system. Lebo ak zdrojom je samotna kin. a pot. energia protizavazia, ta musi byt, ako v kazdej mechanickej sustave, spotrebovana na pracu uzitocnu a stratovu (trenie, teplo, ...).
Dalsia vyrokova perla: "Nejde pochopitelně o žádné perpetum mobile. Pro vynášení se musí energie dodávat (v úplně optimálním případě těch zmíněných 15 kWh/kg)"
Uz v prvom prispevku som poziadal o abstrahovanie samotneho procesu vynasania nakladu. Vam ale nerobi problem to tam strcit naspat a operovat s tym ako so zdrojom energie na zrychlenie nakladu z 500 m/s na 4 km/s.
Ak ale tu energiu beriete aj z protizavazia, kto (co) a ako tu energiu vrati protizavaziu? Mozno si este spominate na otazku na pana Broza, ze ako ma dokaze pritiahnut lanom na lodke, aby sa moja lodka nepohla?
To vsetko su zakladne otazky, na ktore nemate odpoved a ktore z kozmickeho vytahu robia nepouzitelny projekt. Projekt, ktory ma este nevyhodnejsiu energeticku bilanciu, ako raketovy nosic.
Skusim polozit otazku od lesa.
Predstavte si, ze dame na obeznu drahu to protizavazie aj s lanom.
Vsetko pred vynesenim prveho nakladu funguje naprosto synchronizovane.
Otazka znie: "Ako dlho tento system vydrzi letiet po orbitalnej drahe, nez vynesieme prvy naklad?"
Navrhovane anketove odpovede su:
a) 1 mesiac,
b) 1 rok, alebo
c) 1 storocie?
Viete svoju odpoved aj vyargumentovat?
Neskusajte vlozit odpoved d) věčně.
Dakujem vopred za odpoved
Re: Re: Re: Re: Re: Teď
Miroslav Novak,2017-08-22 12:52:06
No a este skusme sustredit na dalsiu podstatnu vec.
Zopakujme si zakladne postulaty:
- zdrojom sily protizavazia je jeho hybnost,
- pri posobeni sily vznika praca,
- tato praca je odoberana hybnosti protizavazia,
- pokles hybnosti protizavazia sa prejavi poklesom obvodovej rychlosti.
Dve otazky:
- co je vo vyssie uvedenej postupnosti chybne?
- akym sposobom dokazeme vratit protizavaziu povodnu rychlost?
Dakujem za odpoved.
Otazky sa rozmnozuju, ale odpovede su v style pana Bilka ignorovane a ignorovane, pripadne parodovane.
Re: Re: Re: Re: Re: Re: Teď
Vladimír Wagner,2017-08-22 13:06:54
Možná se pokusím vypíchnou základní problém ve Vašem uvažování. Cituji Vás: "pri posobeni sily vznika praca". To není pravda. Práce vzniká pouze tehdy, jestliže je výslednice působících sil nenulová a působí po nějaké dráze.
Re: Re: Re: Re: Re: Re: Re: Teď
Miroslav Novak,2017-08-22 13:20:46
ano a tou drahou je popotahovanie toho lana, alebo uz nie? Co ine ste chceli svojim prispevkom ukazat? Ze neviete kam z konopi, tak sa utekate k slovickareniu?
Re: Re: Re: Re: Re: Re: Re: Re: Teď
Peter Handzko,2017-09-03 03:02:40
Pán Novák, myslím že ako experiment k objasneniu princípu vesmírneho výťahu by mohla dobre poslužiť hlava strunovej kosačky. Predpokladám, že vyžínač je všeobecne známi. Podľa Vás zdrojom sily, ktorá napína silon pri kosení a opätovne ho napne aj po kolízii s pevnými predmetmi, je
a) rotujúci pohyb?
c) hybnost udelena silonu pri spustení?
Rotácia bude správne, však? Silon sa nenamotá ani pri spustení z kľudového stavu.
Bé bé bé.... slyším pláč nebo ovci
Petr Jakubec,2017-08-19 06:53:10
U většiny typově podobobných článků na Oslu se v diskuzích u podobných témat ("co kdyby") objevuje prakticky vždy tentýž druh komentářů:
bé - ono to nejde protoze...
bé - ono by se to muselo...
bé - ono by to mohlo...
Nevadí mi, jestli je ono bé bé bé pouze pláčem nad tím, že zatím nemáme dostatečné znalosti a technologie (a třeba je mít ani nebudem), to je dle mého soudu v pořádku, ale ono povestné bé bé bé se mi záhy mění z pláče v bečení ovčí, když z příspěvků pera páně Hrnčiříka se nejsem schopen skrze jeho egocentrickou samolibost pořádně dozvědět co se mi tím "příspěvkem" sakra autor vlastně snažil říci (viz např. blábolení o nunšacích atd.)
Ono slovo "příspěvek" je od slova "přispívat" (pro ty méně zdatné to znamená obohacovat) a z toho mohou posléze mít všichni ostatní "prospěch" a ne být z přispěvků otrávení, to by potom pisatel nebyl přispěvatel, ale .... pan Otrava?
Konec má být vždy pozitivní a proto dík za fajn článek pane Wagnere cítím se Vámi obohacen a rád jsem si s Vámi zalétal na všech orbitách.
Re: Bé bé bé.... slyším pláč nebo ovci
Josef Hrncirik,2017-08-19 09:56:07
S dokonale tuhou věží je to čirá radost bez problémů a hurá na orbity.
Pokud je lano se závažími výrazně lehčí než kabinka, zatížení kabinkou ev. z neodolatelného vábení pokusu o získání zrychlení stoupání kabinky dalším dynamickým tahem za lano bude vítězstvím v přetahování srážka závaží s kabinkou na zemi či pád do blízkosti.
V lepším případě srážka nastane nad zemí.
Pokud jsou vahové kategorie srovnatelné, pak pro zjednodušení předpokládejme např. stejné hmotnosti závaží a kabinky
a start mocným trhem který dostane kabinku na geostacionární dráhu s nedostatečnou rychlostí a závaží udělí impulz směrem k Zemi.
Závaží změní směr a velikost rychlosti z tangenciální (tečné do kolizního kurzu), ale naštěstí? vlivem zvýšení rychlosti i při snižování výšky (uvolněnou potenciální energií) bude obíhat? Zemi po eliptické? orbitě a jakmile lano či řetěz přestane být pokojně geostacionární stane se poněkud nebezpečné.
Vezme sebou do vleku dalším zukamentem zatím prvním skokem odstartovanou kabinku
a co toto bolaso (bola, bolas) či nunčak (nunchaku) udělá netuším, nejsa Nebeský mechanik.
V lepším? případě to celé zůstane na orbitě.
Optimisté pochopitelně napřed vypustí nesmírně těžký systém, kde ztráta geostacionarity působením zanedbatelné kabinky není ihned příliš zřejmá (nekupte to za ty peníze).
Při delší exploataci se to však bude muset nějak řešit třeba klasickým skokem do výšky za utíkajícím balonovým lanem.
Vazba na závaží jen přes lano nakonec ani nečerpá rotační energii ze ze Mě.
Slunce v duši a Damoklovo závaží nad hlavou.
Mor ho!
teplota
Petr Petr,2017-08-18 15:55:37
Je to utopie (a nebezpečná). Podle mého se podceňuje ještě teplota. Nejen ta, že výtah prochází vrstvami s různými teplotami. Ty "velmi nízké energetické nároky, něco okolo 14,8 kWh/kg" znamenají buď výhřevnost větší než methan (jen výhřevnost vodíku je větší - proto palivo raket) nebo ohřátí o mnoho tisíc stupňů. Při jisté účinnosti (třeba ztrátách byť jen 10 %) je to katastrofa. Výtah sice bude teplo rozvádět, ale při své délce a malém průřezu dost neúčinně. Když bude výtah v permanenci tak se uvaří (vypaří) ...
Re: teplota
Josef Hrncirik,2017-08-18 16:05:31
Při malé frekvenci přeběhů Veverek se teplo stačí vyzářit.
Při dobrém mazání a kuličkových ložiskách se teplo prakticky neuvolní a když tak v celém zemském gravitačním poli, kam se ho vejde do Aleluja.
Re: Re: teplota
Petr Petr,2017-08-18 20:59:10
Vyzařováním se odvádí mnohem menší výkon než odvodem tepla vodivostí. To převáží, až když se to rozžhaví. A to je problém výtahu...
Re: Re: Re: teplota
Juraj Chovan,2017-08-19 12:03:36
Konkrétny kúsok lana sa zahreje iba v okamihu prejazdu kabíny, a znovu až za pár dní keď ním prefrčí ďalšia kabína. Takže na odvod tepla vyžiarením má času viac ako dosť. V skutočnosti rádovo viac tepla prijme zo slnečného žiarenia. Ako rozhodne väčší problém vidím odvod tepla z kabíny.
Re: Donald Musk
Josef Hrncirik,2017-08-18 14:20:51
Obludné a kacířské bludy nehezké, hezké mechaniky nebeské.
Představme si, že Nesmírná Vesmírná Inteligence (NSA) umožní Elonovi postavit těžiště Nanejvýš Tuhého Nosníku do geostacionárního oběhu zaměřeného zpočátku kolmo k Zemi.
Mimořádně Tuhý Nosník bude Mimořádně Tvrdošíjně udržovat svůj směr ke Stálicím, ev. pokud bude zcela přesně roztočen, může být stále kolmo k Zemi, jako by byl do ní jednoduše ukotven.
Pokud však po něm poleze do Vesmíru Veverka, začne ho zarážet do Zemí a Nosník začne mířit k jiným Stálicům, prostě přestane to být nejen geostacionární a nastanou podivuhodné Nebeské Úkazy.
Elonovi bude dovoleno vypustit geostacionárně pouze lano (řetěz) položený do geostacionární vrstevnice geostacionární rychlostí (aby nedostal Vesmírným Nunčakem za Ucho).
Pohled na Svíjející a Zmítající Vesmírný Nunčak je ale k nezaplacení.
Spodní články vyrazí horizontálně kruhovou rychlostí, horní však pomaleji.
Rětěz se napne, roztočí a praskne v nejslabším místě, jak předpověděl V.I.Uljanov.
Re: Donald Musk
Vladimír Wagner,2017-08-18 20:12:03
Pochopitelně jde o překlep. Děkuji za upozornění. Člověk při psaní myslí někdy na více věcí najednou, přepíše se a pak už tam při kontrole vidí to správné, i když je tam chyba. Proto je dobré, když má pozorné čtenáře. Poprosím redakci o opravu.
Re: Re: Donald Musk
Josef Hrncirik,2017-08-18 21:18:31
Vedle grafu věta: "Samotná družicová základna je gravitačním centrem systému...", vlastně definitivně zbavuje Zemi geocentricity a umožňuje si kdekoliv vytahovat cokoliv z kohokoliv a nepochybně nese rysy pera mistra Járy da.
Re: Re: Re: Donald Musk
Vladimír Wagner,2017-08-18 21:37:52
Pane Hrnčiříku, Vy dobře víte, že jde o gravitační centru systému výtahu a ne soustavy Země a okolní tělesa. Z Vaši přehršle příspěvků na Oslovi i Vaší afilace je jasné, že máte přírodovědné vzdělání a řadě věcí rozumíte. Ovšem zase z frekvence Vaších příspěvků a hlavně jejich formulování se mi zdá, že si snad musíte léčit nějaké své mindráky. Mě to celkem nevadí, ale zdá se mi, že řadu normálních diskutujících, kteří by normálně měli dotazy, které je zajímají nebo poznámky, může odradit, když na každý dotaz či příspěvek na Oslovi připojí jeden a ten stejný grafoman trollovskou poznámku. Takže si pro jedenkrát přece jen kromě reakce k věci neodpustím osobní poznámku. A doufám, že se alespoň trochu zamyslíte a místo trollování napíšete nějaký zajímavý článek pro Osla ze svého oboru.
Re: Re: Re: Re: Donald Musk
Milan Krnic,2017-08-19 12:03:00
Gravitační centrum reálné, nebo úvahové (pokud uvažujeme pouze systém výtahu a ostatní gravitační působení zanedbáme)?
Vesmírný výtah
Tomáš Pecho,2017-08-18 13:00:40
Pokud bude výtah pouze jeden, tak to je stejné jako když atlet háže kladivem do dálky. Kladivo má vlivem odstředivé síly tendenci vytahovat atleta ze středu jeho rotace. Atlet sice tuto sílu může dorovnat zapřením se o nohy, ale země tuto možnost nemá. Takže jednostranně zbudovaný výtah by vychýlil Zemi ze středu její rotace a toto vychýlení by postupně narůstalo. Výtah jako takový by určitým způsobem ovlivnil i rychlost rotace Země. Otázka je ovšem jestli by to vedlo jen ke snížení rychlosti rotace nebo k jejímu trvalému snižování (k brždění)? Tohle řešení má za mě tedy mnohem více úskalí než jen z čeho to zkonstruovat.
Re: Vesmírný výtah
Josef Hrncirik,2017-08-18 13:32:17
Smysluplně může fungovat pouze Nesmírný Vesmírný Výtah Fungující Jako Nesmírně Tuhý Krakorec a ten na Zemi určitě nebude dříve než Babylonská věž.
Proto se bude rotace Země stále zpomalovat jako doposud hlavně slapovými jevy,
ev. jen poněkud intenzivněji při větším využití přílivových elektráren.
Padající lano
Miroslav Kalina,2017-08-18 11:00:13
Při poškození výtahu nemusí padat pouze kabinka. V případě, že bude hmotnost lana byť jen cca 1kg na metr délky, přeseknutím vlivem kosmického odpadu dojde k jeho přeměně na zátěž o hmotnosti 47.000 tun, padající z výšky geostacionární dráhy..... nemilé..... nechtěl bych pak stát dole ... :-)
Re: Padající lano
Josef Hrncirik,2017-08-18 19:47:46
Proplatí pojišťovna pojistné za ve Všehomíru beze stop zmizelé protizávaží a část lana urvaného nad geostacionární orbitou,
nebo bude logicky vyžadovat doložení trosek?
Re: Padající lano
Vladimír Wagner,2017-08-19 10:47:44
Máte pravdu, že by bylo nutné řešit i problém, že v případě katastrofické události je třeba zajistit, aby části konstrukce nebyly příčinou ohrožení. Částečně lze využít možnosti, že něco shoří v atmosféře a část pak lze řešit nějakým řízeným sestupem či umístěním na stabilní dráhu pro pozdější řešení následků. Ale pochopitelně ani v tomto případě nejde o jednoduchý problém. Jinak katastrofická destrukce marsovského vesmírného výtahu je ve sci-fi formě popsána právě v marsovské trilogii Kim Stanleye Robinsona.
Sen
Jaroslav Pešek,2017-08-18 07:47:03
Vesmírný výtah je sice pěkný sen, ale neproveditelný. To už se spíš dřív začne používat antigravitace, než se vyrobí vesmírný výtah.
Re: Zlý sen
Josef Hrncirik,2017-08-18 08:04:23
Vesmírný výtah má smysl pouze jako tuhý nosník (vrhač oštěpů či handgranátů).
Tuhý nosník potřebné velikosti a tuhosti je ještě větší nesmysl než lano potřebné délky a pevnosti.
Jako Davidův prak to pochopitelně principiálně fungovat nemůže.
Fakir může vylézt nahoru po laně či řetězu.
Musí je však bystře házet pod sebe (jakoby spaliny raketového paliva) a tím se mu špagát krátí.
Re: Sen
Vladimír Wagner,2017-08-18 09:51:27
Otázka proveditelnosti a zvláště pak ekonomické efektivity vesmírného výtahu je stále otevřená. Ale s tou antigravitací nemáte pravdu. Mezi antigravitací a vesmírným výtahem je jeden podstatný rozdíl. Současná fyzika antigravitaci nedovoluje a je otevřená otázka, zda je vůbec fyzikálně možná. Vesmírný výtah neodporuje žádnému fyzikálnímu zákonu a principiálně je proveditelný. Otevřené otázky jsou "pouze" technologické. Tedy, jestli se podaří zajistit potřebné materiály v potřebném množství a s dostatečně nízkými náklady. A také, zda vesmírné aktivity budou příslušnou prioritou lidstva a dané dosažené technologie umožní konkurenceschopnost vesmírného výtahu s jinými variantami dopravy nákladů na oběžnou dráhu.
Re: Re: Sen
Milan Krnic,2017-08-18 12:50:55
Principiálně teoreticky jistē. Když vhodnē omezíme realitu.
Re: Re: Sen
Jaroslav Pešek,2017-08-18 14:02:46
Tou antigravitací jsem chtěl naznačit, jak neproveditelné to je.
Re: Sen
Zab Hazar,2017-08-19 10:43:48
Myslím si totéž. Když totiž nadšenci horující pro výtah konečně pochopili, že jakákoli geostředná síla působící na obíhající těleso bude nevyhnutelně snižovat jeho perigeum, až nakonec buďto spadne nebo se utrhne, přišli mazaně s protizávažím. Jenže imho zapomínají na to, že i u protizávaží bude ten samý efekt: každé zatížení stanice trochu popotáhne i protizávaží, a výsledek bude stejný. Jediná šance je, umístit na protizávaží vyrovnávací reaktivní motory, jež by dorovnávaly deficit ve výšce a oběžné rychlosti - jenže to pak samotné protizávaží ztrácí smysl, neboť ty motory mohou být vlastně rovnou na té stanici. Prostě, fyzika fakt nejde očurat a lidi, co si pod vesmírným výtahem představují sebe v dětských letech, jak kolem prstu točili železnou matku na nitce a ona nespadla a neodletěla, jsou trochu mimo mísu :-)
tržná délka
Tomáš Vodička,2017-08-18 03:39:46
Mám otázku: jestliže (teoretická) maximální tržná délka lan z grafenových nanotrubiček má být kolem 5000 km, je to pořád málo. Pokud chápu, pro výtah z povrchu Země bychom potřebovali tržnou délku skoro o řád vyšší, nebo ne?
Také tam musí být značná rezerva, kvůli dynamickému namáhání, atd.
Existuje nějaký vědecky fundovaný odhad, jaká je teoretická maximální pevnost obecného materiálu, tedy maximální možná tržná délka? Z hlediska fyziky atomárních sil?
Re: tržná délka
Josef Hrncirik,2017-08-18 07:20:06
Pevnost (tržná síla (napětí) na plochu původního průřezu)
má rozměr síla/plocha, tj. tlak, tj. deformační energie/objem deformovaného vzorku, tj. dosažitelná hustota deformační energie.
Deformace materiálu při přetržení či rozdrcení (roztečení tlakovou silou) či analogicky při protažení obvykle nepřesahuje 100%.
Potom lze brát jako horní hranici pevnosti snadno měřitelný modul pružnosti E či G.
Pravděpodobnější je, že již při deformaci 10% dojde ke vzniku fatálních poruch ve struktuře a lavinovitě se šířícímu porušení, tj. překročení pevnosti.
Totální rozpad pevnosti materiálu je určitě jeho sublimace či roztavení.
Horní hranice pevnosti tedy musí být menší než objemová hustota tepla tání či sublimace.
Tyto hodnoty či pevnost chemické vazby lze měřit či spolehlivě odhadnout a simulanti je běžně modelují.
I zde platí "Diamanty ničím nenahradíš".
Maximalistický materiál (hypotetické vlákno řetězců lineárně pospojovaných ...=C=C=... nemůže být pevnější více než 2x než ideální vlákno diamantu či hahaha PE řetězce či řekněme 1,5 než C nánotrubička.
Zanechte bláhových nadějí.
Největší hustotu sublimačního tepla má uhlík, proto je výborný pro výrobu ablativních štítů MIRV.
Howgh.
Shalom.
Re: tržná délka
Tomáš Pilař,2017-08-18 07:31:57
Je to trochu míň zlé, než se zdá, protože se lano může mít proměnnou tloušťku (nejsilněší na geostacionární dráze). To že jsme od použitelného lana hodně vzdáleni platí, protože lano musí být "vesmíru odolné" (UV záření, mikrometeority....). Vesmíru odolnost je možná ještě větší problém než tržná délka, kterou lze trochu oblafnout proměnou tloušťkou.
Re: tržná délka
Vladimír Wagner,2017-08-18 10:29:24
Jak už bylo zmíněno, část Vámi zmíněného problému řeší postupné zvětšování tloušťky lana směrem ke geostacionární základně. V principu by tak stačily i současné materiály, ale musely by mít tloušťku nesmyslně velkou. Další jev, který zlepšuje situaci, je snižování tíhové síly se zvětšováním vzdálenosti od povrchu Země.
Poděkování
Mintaka Earthian,2017-08-17 23:06:18
Děkuji za přínosný článek. Toto téma mě obzvláště zajímá.
Pokud už máme materiály pro postavení na měsíci, jaký objem/hmotnost materiálu by bylo třeba dopravit k měsíci, aby tam bylo možné výtah postavit?
tržná délka
Florian Stanislav,2017-08-17 22:45:37
Článek :
" Pro srovnání, pro kovy jako titan, ocel nebo hliník je to mezi 20 až 30 km,.."
https://cs.wikipedia.org/wiki/Tr%C5%BEn%C3%A1_d%C3%A9lka
Hliník má tržnou délku asi 3,4 km, myslí se asi dural 18,9 km.
Kovová lana nemají podstatně větší tržnou délku jak přírodní vlákna, kde nejlepší vlastnosti má hedvábí a pavučina.
Tržná délka bavlny je myslím 15 km a konopí 30 km. U přírodních vláken záleží na vlhkosti.Přírodní vlákna se zakrucují ( spřádání), syntetická vlákna se musí dloužit, to je zrovnoběžnit makromolekuly ke zvýšení mezimolekulových sil.
Nikde jsem se zatím nedočetl, že by někdo z nanovláken grafenu vyrobil třeba 1 km dlouhé lano (100- 200 x pevnější jak ocelové).
Re: tržná délka
Vladimír Wagner,2017-08-18 10:21:33
Máte pochopitelně pravdu, u těch kovových materiálu jsou přirozeně myšleny jejich optimálnější formy. Z nanovláken grafenu se nepodařilo vyrobit ani lano o metrové délce. Zatím se daří pouze řádově jednodušší a menší struktury. K lanům o kilometrových délkách je ještě hodně daleko (třeba ne časově, ale technologicky). Je třeba zdůraznit, že této oblasti je věnována extrémní pozornost, protože grafen má obrovský potenciál využití v řadě oblastí.
Jiří Hejl,2017-08-17 21:19:20
Nikde není žádná zmínka o tepelné dilataci lana ze slunce do stínu země. Při uvažované délce lana by byl rozdíl v délce ohromný - řádově v kilometrech - a vyvolal při veliké napětí v tahu při přechodu do stínu a skokové uvolnění při zahřátí. Náklad na laně by se v důsledku coriolisova zrychlení rozkmital.
Re:
Vladimír Wagner,2017-08-18 10:25:11
Pochopitelně i tento problém patří k technologickým překážkám, které je potřeba řešit. Jak bylo v textu zmíněno, struktura musí počítat s kmity i vyvažování řady změn v její délce i rozložení hmotnosti, ke které vede více procesů, nejen Vámi zmíněné tepelné namáhání.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce